斜切截平面法求解圆管斜交圆锥管相贯线

利用斜切截平面求做相贯线

1）做一圆管斜交圆锥管的主、俯两视图，并在锥底两端标注A点和B点，锥顶标为O点（见图2-189）。

2）在俯视图中把圆锥管底圆十二等分（等分数越多，俯视图中圆锥管被斜切的截面近似圆投影越准确），在圆周线上得交点为1、2、3、4、5、6、7、6、5、4、3、2点，过圆周线上这些点引素线与锥顶O点相连。

3）过俯视图中锥底圆周线上的等分点向上往主视图引垂线垂直于主视图锥底线段AB，垂线交于锥底线段AB上的交点为1、2、3、4、5、6、7点。过锥底线段AB上的1、2、3、4、5、6、7点引素线与主视图上的锥顶O点相连。

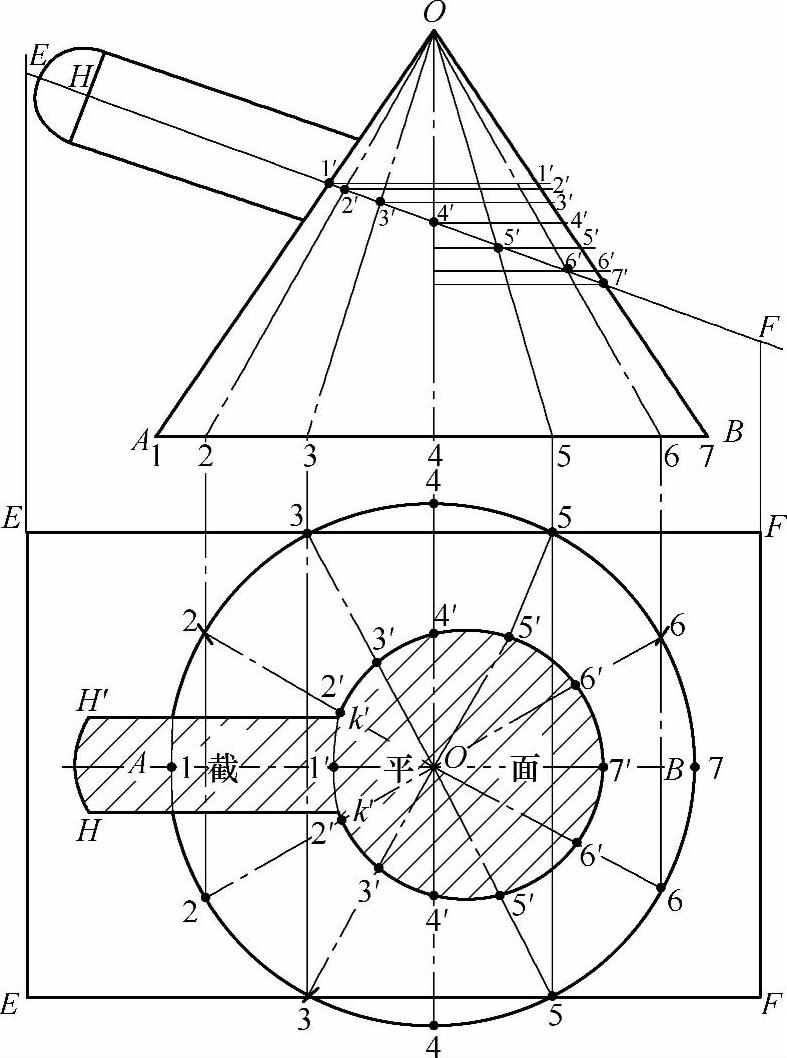
图2-189 圆管斜交圆锥管斜切的截平面

4）在主视图上做一条斜切切割线EF。斜切切割线切割圆管的中轴线，并过主视图圆锥管上的各条素线，其中：过素线O-1，在素线O-1上得交点为1′点；过素线O-2，在素线O-2上得交点为2′点；过素线O_-3，在素线O-3上得交点为3′点；过素线O-4，在素线O-4上得交点为4′点；过素线O-5，在素线O-5上得交点为5′点；过素线O-6，在素线O-6上得交点为6′点；过素线O-7，在素线O-7上得交点为7′点。

各条素线上的交点，即1′、2′、3′、4′、5′、6′、7′点，就是斜切割线EF切割圆锥管、在圆锥管体表面上的被切割点。(www.xing528.com)

5）过主视图上各条素线上的被切割点，即1′、2′、3′、4′、5′、6′、7′点，做平行线平行于锥底线段AB。七条平行线过素线O-4，交于圆锥管边线OB上，在圆锥管边线OB上得交点为1′、2′、3′、4′、5′、6′、7′点。

6）在俯视图中以O点为圆心，以主视图中七条平行线在圆锥管边线OB上交点至素线O-4上交点的平行线长为半径分别画弧，其中：①以主视图1′点平行线在圆锥管边线OB上交点至素线O-4上交点的平行线长为半径所画弧线交俯视图素线O-1上的交点为1′点。②以主视图2′点平行线在圆锥管边线OB上交点至素线O-4上交点的平行线长为半径所画弧线交俯视图素线O-2上的交点为两个2′点。③以主视图3′点平行线在圆锥管边线OB上交点至素线O-4上交点的平行线长为半径所画弧线交俯视图素线O-3上的交点为两个3′点。④以主视图4′点平行线在圆锥管边线OB上交点至素线O-4上交点的平行线长所画弧线交俯视图素线O-4上的交点为两个4′点。⑤以主视图5′点平行线在圆锥管边线OB上交点至素线O-4上交点的平行线长为半径所画弧线交俯视图素线O-5上的交点为两个5′点。⑥以主视图6′点平行线在圆锥管边线OB上交点至素线O-4上交点的平行线长为半径所画的弧线交俯视图素线O-6上的交点为两6′点。⑦以主视图7′点平行线在圆锥管边线OB上交点至素线O-4上交点的平行线长为半径所画弧线交俯视图素线O-7上的交点为7′点。

7）把俯视图中各条素线上的交点，即1′、2′、3′、4′、5′、6′、7′、6′、5′、4′、3′、2′点，用曲线圆滑连接，所得近似圆就是圆锥管被斜切割后，在俯视图中的截面投影。圆管中轴线上切割线EF切割圆管，在俯视图中圆管截面上所得两条边与近似圆相交，在近似圆上得到两K′点，那么这两个K′点即是圆管与圆锥管相交的两个相贯点。

【小结】

从以上所做的圆管斜交圆锥管的相贯线的过程中，我们看到圆锥管被切割后，反映在俯视图中的截平面是一个近似圆；而圆管被切割后，反映在俯视图中截平面是两条边夹一个面。那么，圆管截平面的两条边与圆锥管截平面的近似圆圆周线上的两个交点（即俯视图中的两个K′点）即是两管的相贯点。在主视图上一条切割线即俯视图上的一个切割面，在俯视图中即可得两个相贯点。为求做两管不对称相交构件的相贯线，就得在主视图上适量地做些切割线（越多越准确），这样才能在俯视图中得到相应数量的相贯点。

求做两管相贯线，主要是把斜切主圆锥管的截平面的部分曲线求做出，这样问题就迎刃而解了。因为支管的截平面是两条边夹一面，所以在做图过程中直接就可以做出。支管的截平面上的两条边与主圆锥管截平面的近似圆相交，相交点就是相贯点。在求做两管相贯线时，根据支管与主圆锥管相交在俯视图中的位置判断，可做（支管相交主圆锥管半圆周上）近似圆的半圆曲线，或（支管相交主圆锥管1/4圆周上）近似圆的1/4曲线。利用这一规律，我们就可以做出一些比较复杂、麻烦、不对称两管相交的相贯线，且用这一方法求做两管不对称相交构件相贯线，就叫斜切截平面法。