圆锥台展开图的制作方法

已知圆锥台底圆直径为50，上圆直径为30，高为30，求做其展开图。

1.用三角形展开法求做圆锥台的展开

（1）做图思考与分析

1）利用已知条件做出立体图和主、俯两视图（见图2-82）。

2）因为圆锥台形体表面不存在相互平行的素线，所以不适合用平行线法做展开。

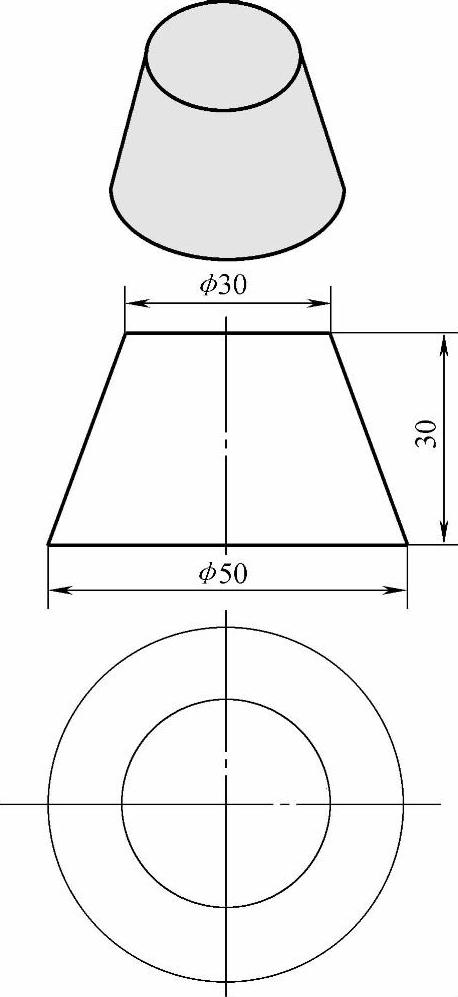
图2-82 圆锥台的立体图和主、俯两视图

3）如果用三角形法做展开，那么就得把视图的图形分成若干个三角形。为了做图方便，我们统一圆锥台表面分成两种样式的小三角形，那么就得在俯视图中把圆锥台十二等分。因为只需标出一半，即可对应主视图，所以圆锥台标出六个等分点即可。圆锥台底圆上六个等分点为1′、3′、5′、7′、9′、11′、13′点，圆锥台上圆上六个等分点为2′、4′、6′、8′、10′、12′、14′点。用线段连接1′点至2′点、3′点至4′点、5′点至6′点、7′点至8′点、9′点至10′点、11′点至12′点、13′点至14′点，相连后的这些素线的实长都相等。

4）过俯视图中的各素线点向主视图引上垂线，与圆锥台底圆线段及上圆线段垂直相交得各对应交点。对应连接各交点后得到主视图中的素线1-2、3-4、5-6、7-8、9-10、11-12、13-14，七条素线把圆锥台分成六个部分的实际图形都是一样的。为求做展开图，还得把这六个部分变成小三角形的样式。要想变成三角形，每个部分就得做一条辅助线，使每个部分成为两个三角形。做辅助线把2点至3点、4点至5点、6点至7点、8点至9点、10点至11点、12点至13点相连，六条辅助线在主、俯两视图中一一对应，共做出两种样式的小三角形，每种样式六个，在主视图上共计有十二个小三角形。

求出这十二个小三角形的实际图形，把它展现在一个平面上，就是这个圆锥台的半个展开图，再做另一半就是整个圆锥台的展开实际图形。

（2）展开步骤

1）按已知条件做出主、俯两视图。

2）把俯视图中的圆锥台十二等分，其中一半为六等分，圆锥台底圆上六个等分点为1′、3′、5′、7′、9′、11′、13′点，上圆上六个等分点为2′、4′、6′、8′、10′、12′、14′点。做素线连接1′点至2′点、3′点至4′点、5′点至6′点、7′点至8′点、9′点至10′点、11′点至12′点、13′点至14′点，得七条素线。用三角形展开法作图，就得把每个等分的形状变成两个小三角形，要想变成小三角形，就得在每个等分中做一条辅助线，辅助线为2′点至3′点、4′点至5′点、6′点至7′点、8′点至9′点、10′点至11′点、12′点至13′点，共计六条辅助线。每条辅助线都相等，因此它们的实长也相等。

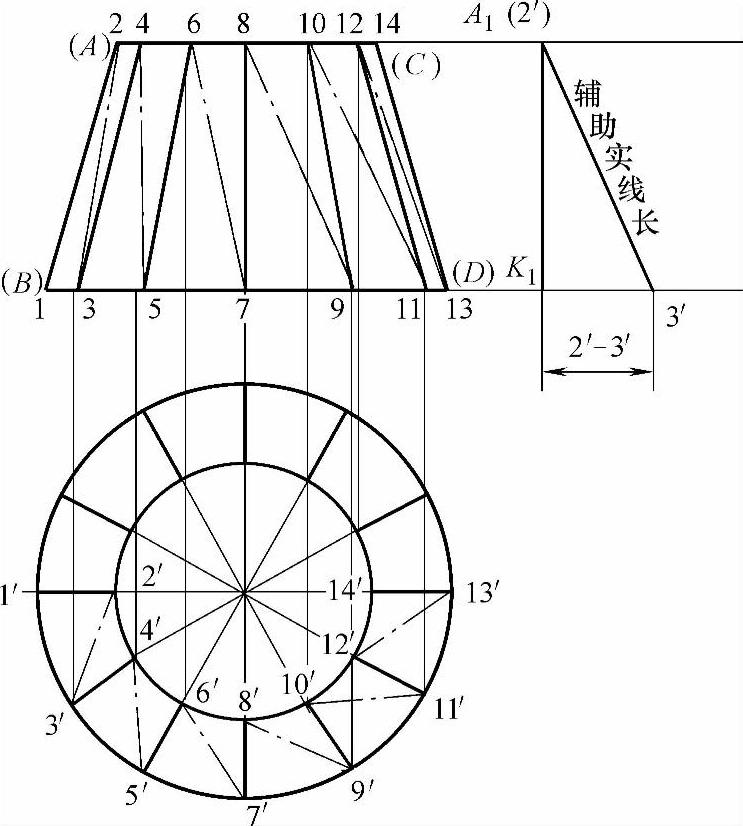
3）辅助线实长求法：①向右引主视图圆锥台底圆线段BD和上圆线段AC的延长线，在BD的延长线上选一点K₁，过K₁点做延长线的垂线A₁（2′）K₁，垂线与AC延长线交于A₁（2′）点。②以主视图底圆线段BD延长线上K₁点为圆心，俯视图中辅助线2′-3′为半径画弧，弧线与线段BD延长线交于3′点。用线段连接2′点至3′点，所得斜线段长就是俯视图中辅助线2′-3′的实长，即所有辅助线的实长（见图2-83）。

4）展开：①以主视图中素线1-2为基准线。以基准线上1点为圆心，俯视图中底圆的一等分（即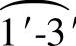的弧长）为半径，往基准线两边画弧；再以基准线上2点为圆心，俯视图中辅助线2′-3′的实长为半径画弧，与刚才的两个弧分别相交得交点为两个3点，用点画线连接2点至3点。②以基准线上2点为圆心，俯视图中上圆的一等分（即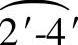的弧长）为半径，往基准线两边画弧；再以两个3点为圆心，主视图中素线1-2为半径画弧，与刚才两弧分别相交的交点为两个4点，用线段连接3点至4点。③因为素线实长都相等，辅助线实长也都相等，所以用同样方法继续做下去，再把底圆和上圆的各点用曲线圆滑连接起来，即得圆锥台的展开图形（见图2-84）。

(www.xing528.com)

图2-83 圆锥台的素线、辅助线和辅助线的实长

2.用放射线展开法求做圆锥台的展开

（1）做图思考与分析

从圆锥台的立体图和主、俯两视图中看到圆锥台形体表面各条素线的延长线交于一点，所以适宜用放射线法展开。

（2）展开步骤

1）按已知条件画出主视图。

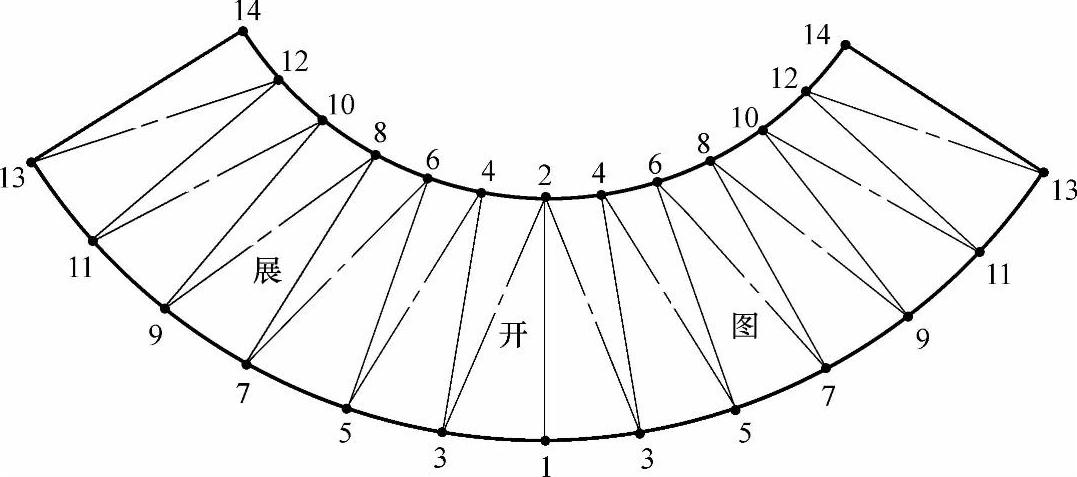
图2-84 用三角形展开法所做的圆锥台展开图

2）做圆锥台两边线AB与CD的延长线，它们相交于点O。

3）以O点为圆心，OA为半径画弧；再以O点为圆心，OB为半径画弧。

4）在以OB为半径所画弧线上任取一点为起点，以圆锥台底圆十二等分的一份弧长为半径，顺次在此弧线上截取十二次，此时所截弧线的长等于圆锥台底圆的周长，最后的截取点为13。

5）用线段连接O点至13点、O点至1点，那么这两条直线所截取的两条弧线所夹的图形就是圆锥台的展开图形（见图2-85）。

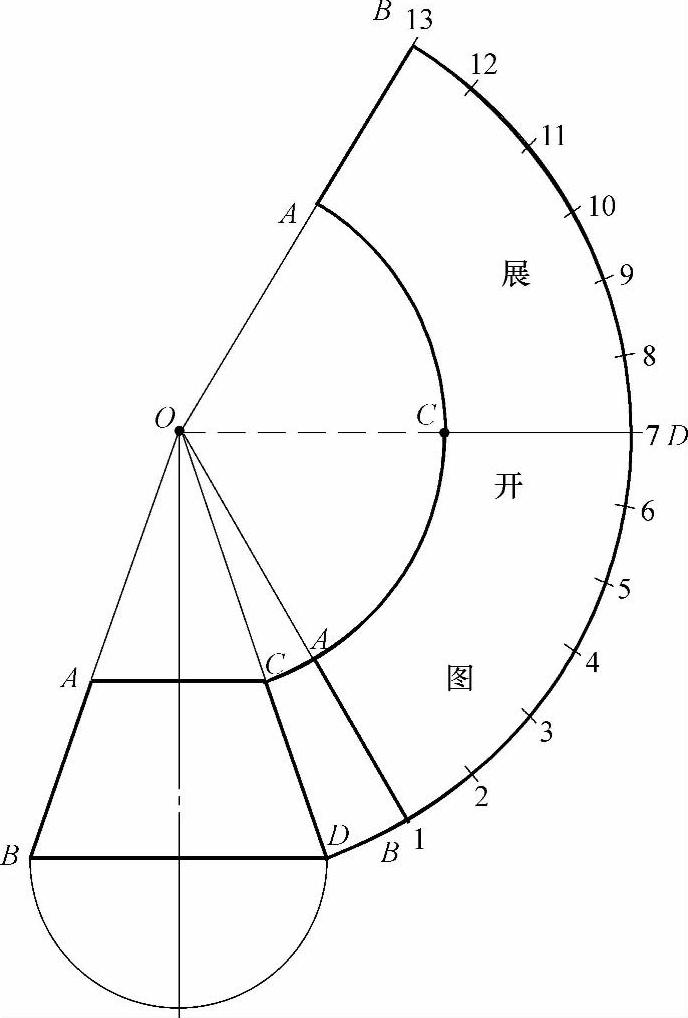
图2-85 用放射线展开法所做的圆锥台展开图