比较不同方法的钣金构件相贯线求做

以上所介绍的三种求相贯线方法的共同点都是根据构件相贯的特点，用不同的方法找出构件两形体表面相贯的共同点（即相贯点），以获得相贯线。同一种构件求做相贯线，可以采取多种方法，具体采用哪一种方法比较方便和省事，下面举例做分析。

【举例17】 圆管正交圆锥管，求做相贯线。

1.素线法求做相贯线

（1）思考与分析

1）因为左视图中圆管垂直于圆锥管投影面，所以圆管上的各条素线也都垂直于圆锥管的投影面，圆管的各条素线在圆锥管投影面上都积聚成点。把这些积聚成点的素线点连接起来就组成了一个实形圆（即圆管），这个在左视图中的实形圆图即为圆管正交圆锥管两管相交的相贯线，且为已知，可以直接在视图中做出。

2）要想利用素线法求做主视图中两管相交的相贯线，就得借助左视图中的已知条件，即左视图中两管相交的相贯线。

3）把相贯线分成若干个相贯点，锥顶引素线通过若干个相贯点，交于锥底圆线段上，利用做三视图中的主俯长对正、主左高平齐、左俯宽相等的特性，一一对应各条素线在各视图中的相对应位置，以求得主视图中各条素线的相贯点。

（2）求做步骤

1）做出主、俯、左三视图（见图2-69）。

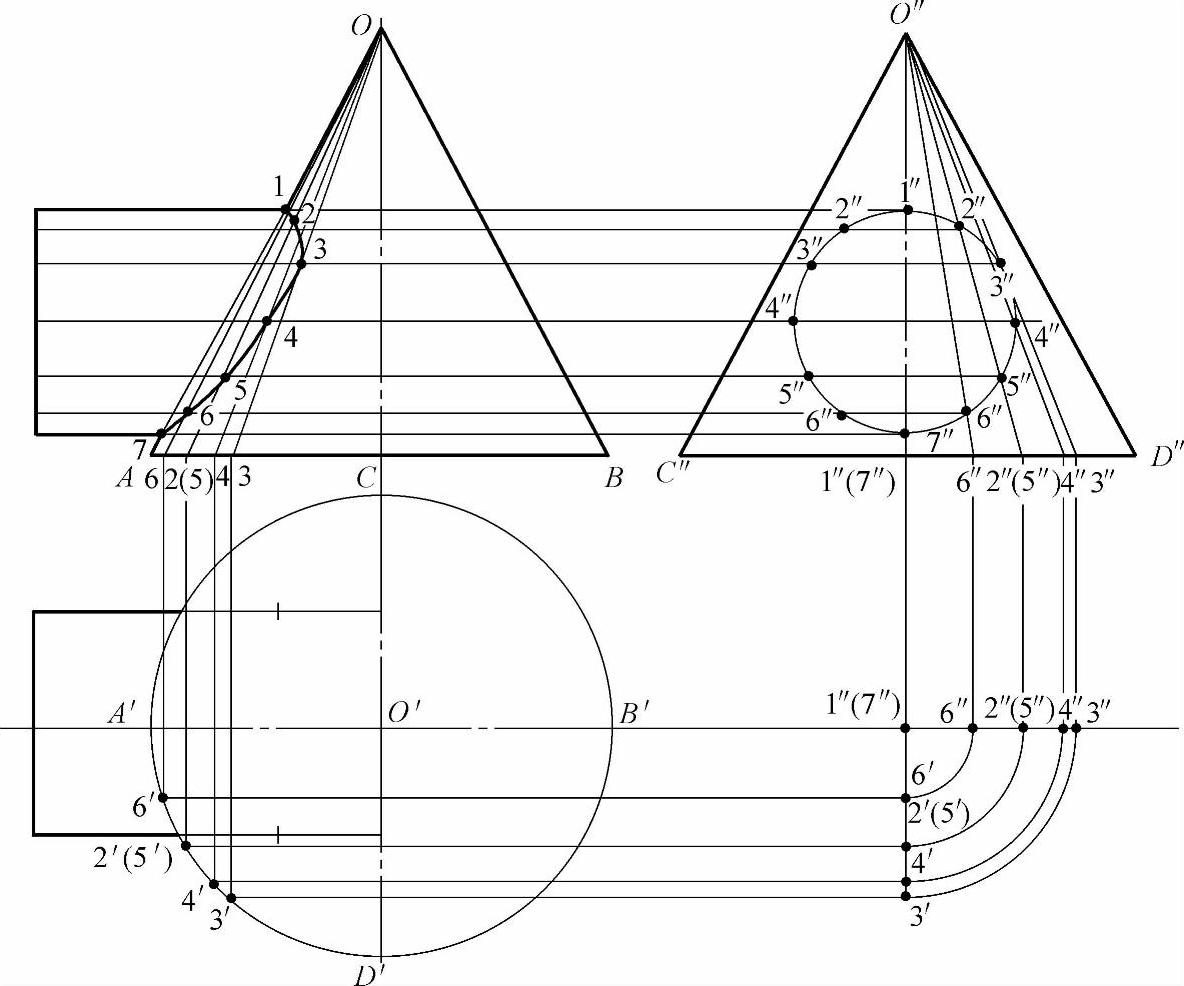
图2-69 素线法求做圆管正交圆锥管的相贯线

2）把左视图中的实形圆分成十二等分，等分点为1″、2″、3″、4″、5″、6″、7″、6″、5″、4″、3″、2″点。这些等分点中1″点为主视图相贯线上的最高点，7″点为主视图中相贯线上的最低点，4″点为主视图相贯线上的最前点与最后点，2″、3″、5″、6″点为主视图相贯线上的一般过渡点。

3）在左视图上从圆锥顶O″点过1″、2″、3″、4″、5″、6″、7″点分别引素线，与圆锥底线段C″D″交于1″（7″）、6″、2″（5″）、4″、3″点，其中1″点与7″点的素线重合，所以得交点为1″（7″）点；2″点与5″点的素线重合，所以得交点为2″（5″）点。

4）过左视图中圆锥底线段C″D″上的这些交点做下垂线，与俯视图中1′（7′）点至O′点素线向右引的延长线交于1″（7″）、6″、2″（5″）、4″、3″点。这些点在延长线各个交点之间的长度，即为左视图中各素线在圆锥底的宽度，即俯左宽相等。

5）以左视图上1″（7″）点的下垂线上的点1″（7″）为圆心，以各条素线在圆锥底线段C″D″上的各自宽度为半径画弧，弧线与左视图上1″（7″）点的下垂线交于6′、2′（5′）、4′、3′点。过这几个点做锥底线段C″D″的平行线，与俯视图圆锥底圆周线上交于6′、2′（5′）、4′、3′点。

6）过俯视图锥底圆周线上这几个点做上垂线，与主视图锥底线段AB交于6、2（5）、4、3点。过这几个点做素线与锥顶O点相连。

7）过左视图中圆管实形圆的各等分点做锥底线段C″D″的平行线，平行线与主视图上各条素线对应相交，得各对应交点为1、2、3、4、5、6、7点。用曲线圆滑连接这些点，即得主视图上的相贯线。

2.截平面法求做相贯线

（1）思考与分析

1）由于圆管正交圆锥管，所以水平切割圆管时同时水平切割圆锥管。被切割圆管在俯视图投影是矩形，被切割圆锥管在俯视图投影是圆形。圆的矩形投影两条边与圆锥管圆形投影相交点，即是两管相交的相贯点。

找出两管相贯的特殊点（即最高点与最低点），最前点与最后点和若干个一般过渡点。在这些点上进行平面切割，以找出俯视图中两管相交的相贯点，用曲线圆滑连接这些相贯点，即得俯视图中两管相交的相贯线。

2）把俯视图中的各个相贯点往主视图上引上垂线，上垂线与主视图上的水平切割线一一对应相交，得到的交点即为各自的相贯点。用曲线圆滑连接这些相贯点，即得主视图中两管相交的相贯线。

（2）求做步骤

1）做出主、俯两视图（见图2-70）。(www.xing528.com)

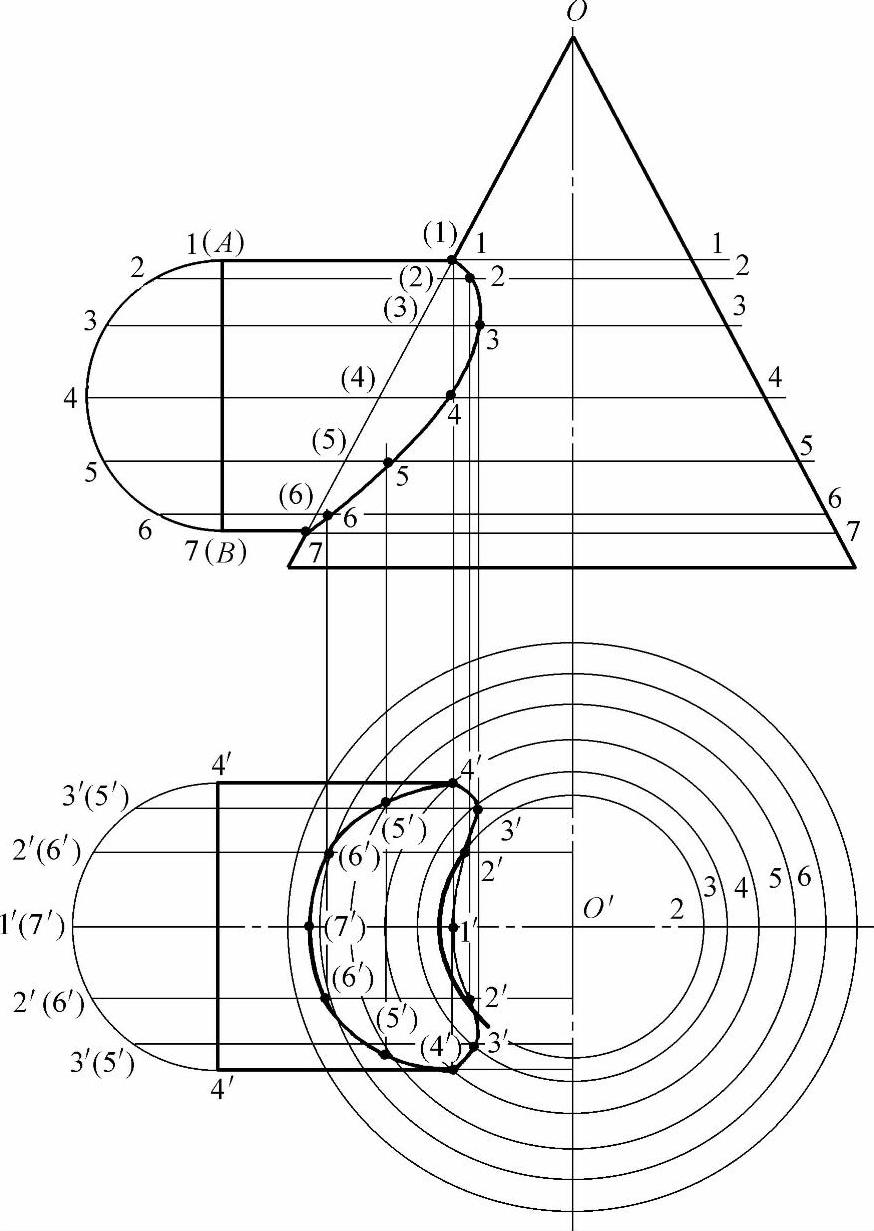
图2-70 用截平面法求做圆管正交圆锥管的相贯线

2）在主视图圆管端线段AB上做半圆，并把半圆六等分，等分点为1、2、3、4、5、6、7点，过这七个等分点做水平切割线，交圆锥管两边线的交点（各两个）为1、2、3、4、5、6、7点。

3）在这七条切割线上，其中两个1点为切割相贯线上的最高点，两个7点为切割相贯线上的最低点，两个4点为切割相贯线上的最前点与最后点，两个2、两个3、两个5、两个6点为切割相贯线上的一般过渡点。因为最高点与最低点都为已知，所以不必再求做。

4）以俯视图中的O′点为圆心，分别以主视图中切割线2-2、3-3、4-4、5-5、6-6的1/2为半径画圆。

5）在俯视图中的圆管端做半圆，并把半圆六等分，等分点为4′、3′（5′）、2′（6′）、1′（7′）、2′（6）′、3′（5′）、4′点。过这些等分点做圆锥管底线段的平行线，平行线与俯视图中各个切割圆对应相交，得对应点为两个2′、两个3′、两个4′、两个5′、两个6′、两个1′、两个7′点。这些点即是俯视图中相贯线上各自的相贯点。

6）过俯视图中各相贯点做上垂线，与主视图各切割线对应相交，得各对应交点为2、3、4、5、6点。因为最高点1与最低点7为已知，那么用曲线把1、2、3、4、5、6、7点圆滑连接起来，就是主视图中两管相交的相贯线。

3.球面法求做相贯线

（1）思考与分析 因为两管轴心线同时相交于同一个点，所引可以利用球面法。做一个视图，即主视图。以两管轴心线交点为圆心，适当多地做圆，每个圆的圆周线同时经过圆管两边和圆锥管两边，在圆管两边和圆锥管两边各得两个交点。做圆管两边交点的切割线，再做圆锥管两边交点的切割线，同一个圆周线上两条切割线相交，相交点就是两管结合的相贯点。把适当多做的圆周线上圆管切割线与圆锥管切割线它们的交点相连，就组成了一个两管相交的相贯线。因为相贯线上最高点和最低点为已知，不必再求做，但是其他相贯线上的特殊点，即最前点与最后点，只能是靠求做一般过渡点连线大致求做出。

（2）求做步骤

1）做主视图（见图2-71）。

2）把圆管端线段AB适当四等分，等分点为1、2、3、4、5点，过其中三个点（即2点、3点、4点）做三条水平切割线，这三条切割线交于圆锥体的两边线的交点（各两个）为2′、3′、4′点。

3）以两管轴心线交点O点为圆心，O点至圆锥体边线上的切割线交点（即2′、3′、4′点）的长为半径分别画圆。这三个同心圆的圆周线，经过圆管边线及其延长线，得交点（各两个）分别为2″、3″、4″点。切割线2″-2″、3″-3″、4″-4″与三条水平切割线对应相交，得各对应交点为2、3、4点，那么用曲线把1、2、3、4、5点圆滑连起来，即得两管相交的相贯线。

从以上三种方法求做相贯线的步骤中，我们看出球面法比截平面法简单方便，而截平面法又比素线法简单方便。但三种方法又有各自的条件，如果离开各自的条件，将无法完成相贯线的求做，如：球面法适用于两旋转体，且轴心线相交于一点，否则无效；素线法得利用其视图中的已知条件（即已知相贯线），才可以求做出主视图中的相贯线。只有截平面法不受条件限制，可以通过水平面切割、垂直面切割或倾斜面切割来求做相贯线。

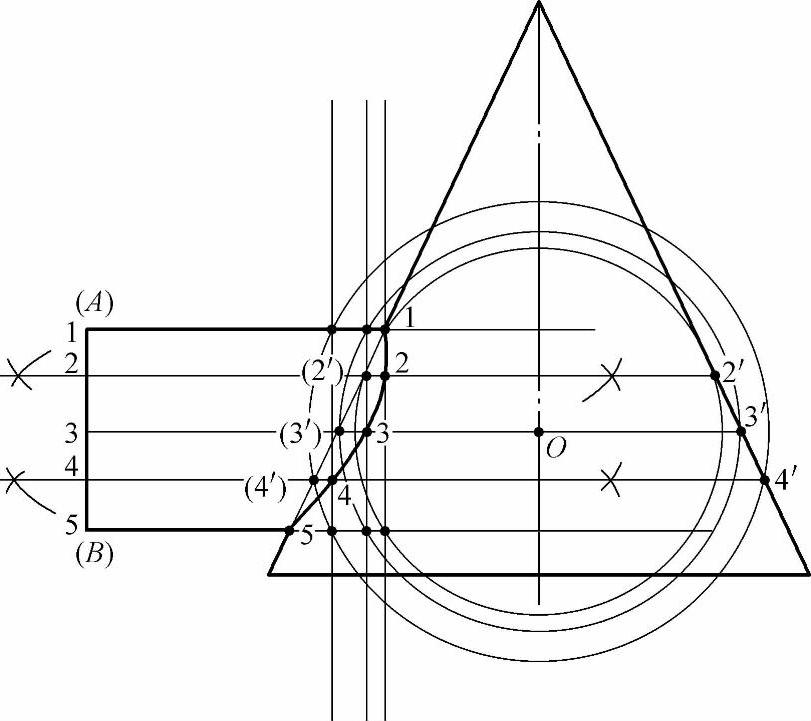
图2-71 球面法求做圆管正交圆锥管的相贯线

【小结】

求做各种钣金构件的相贯线时，具体需要采用哪一种方法比较简单、方便和省事，要根据各种钣金构件相贯的条件进行具体分析与考虑。

表2-1列出选择求各种钣金构件相贯线的方法，可供参考。

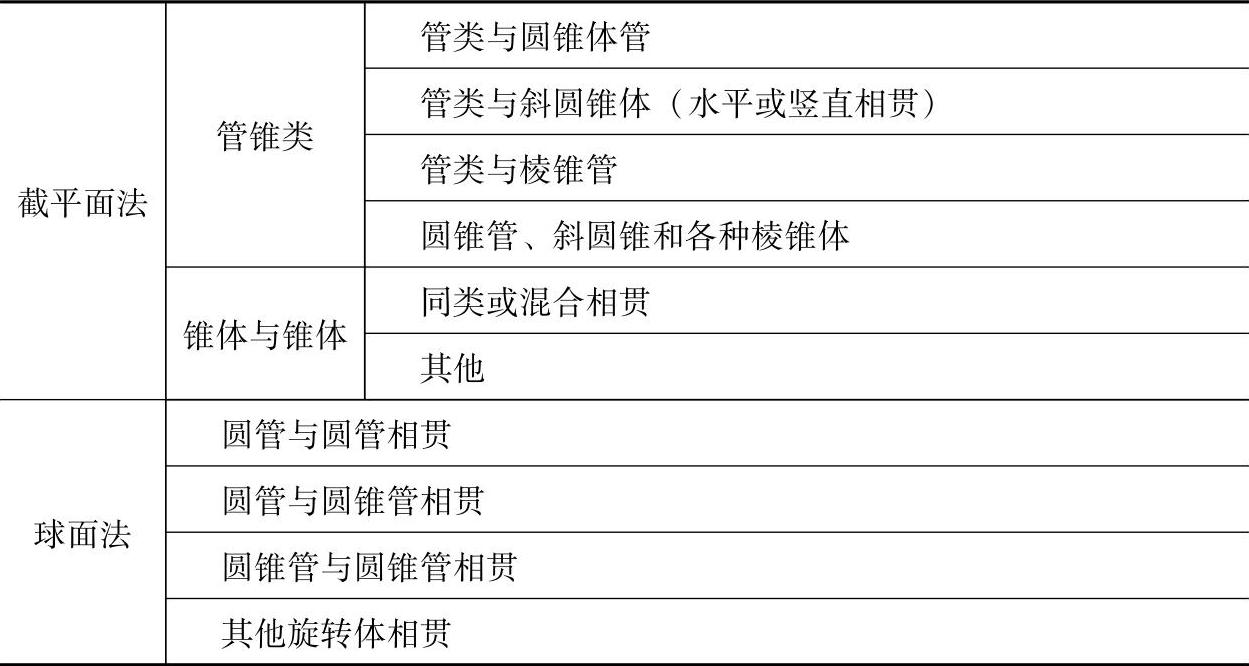
表2-1各种钣金构件相贯线的方法

（续）