放样图的实长线求解方法

（直角三角形做图法、计算法）

1.线段在视图中的投影特征

求线段实长对钣金展开来说十分重要。我们知道钣金构件制作前第一道工序就是按构件图样进行放样，然后才能进行下一道工序。放样图与视图不同，放样图是构件表面的展开图，在展开图中所有图线（轮廓线、棱线、辅助线及做图线等）都是构件表面对应部分的实长线。这些线（如天圆地方和各种过渡接头等）在一些视图中往往不反映实长，放样时必须先求出那些不反映实长线段的实长来，才能做展开图。

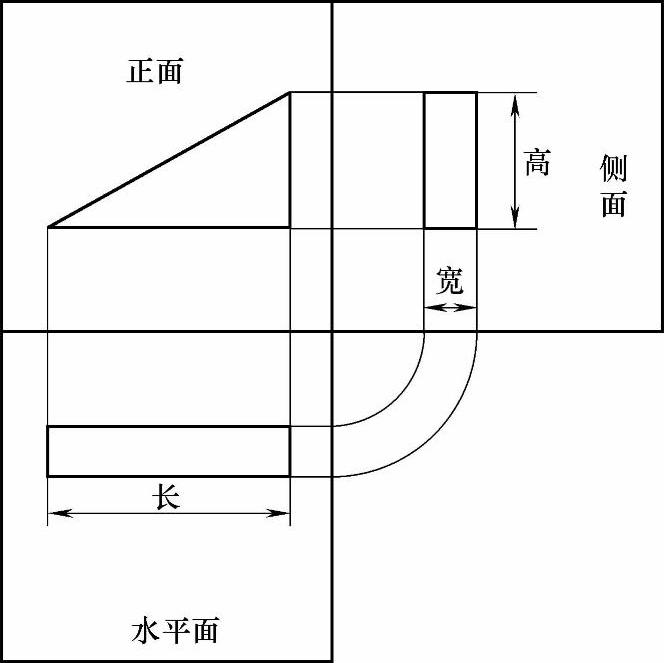
图2-3 三角块在三视图中的投影

如何在视图中识别哪些线段（棱线或做图线）反映实长，哪些不反映实长，这是在求实长线前必须首先要解决的问题。只有解决此问题，才能着手求出那些不反映实长线段的实长来。

线段实长鉴别法：线段是否反映实长，可依据线段投影特性来识别。

（1）垂直线 在三视图中，当线段垂直于某一投影面时，则它必然平行于另外两投影面。因此该线段在另外两投影面上反映实长（见图2-4）。

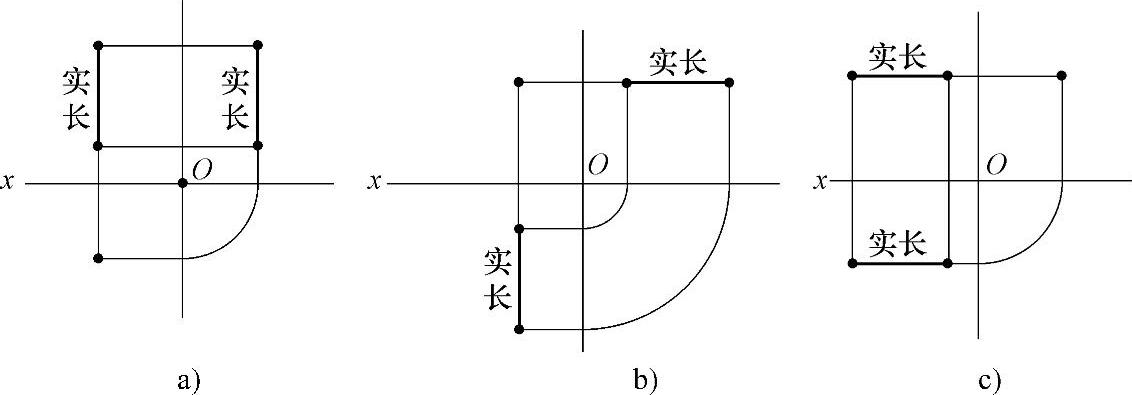
图2-4 垂直线在三视图中的投影

a）铅垂线 b）正垂线 c）侧垂线

1）铅垂线：水平面上投影成点，正面投影和侧面投影反映实长（见图2-4a）。

2）正垂线：正面投影成点，水平面和侧面投影反映实长（见图2-4b）。

3）侧垂线：侧面投影成点，正面和水平面投影反映实长（见图2-4c）。

（2）平行线 当线段平行于某一投影面，而倾斜于另两投影面时，则该线段在所平行的投影面上的投影反映实长，在另外两投影面上的投影比原实长短（见图2-5）。

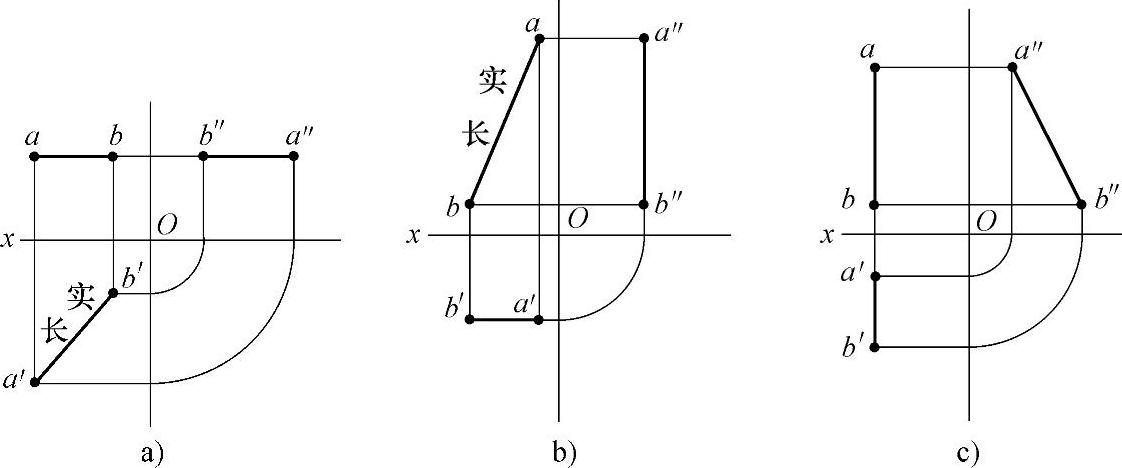
图2-5 平行线在三视图中的投影

a）水平线 b）正平线 c）侧平线

1）水平线：当线段ab平行于投影面水平面（即俯视图）时，它在俯视图中是倾斜的实长线，在另外两视图中（即主视图和左视图中）是平行于x轴的平行线（见图2-5a）。

2）正平线：当线段ab平行于投影面正面（即主视图）时，它在主视图中是倾斜的实长线，在俯视图中是平行于x轴的平行线，在左视图中是垂直于x轴的垂直线（见图2-5b）。

3）侧平线：当线段ab平行于投影面侧面（即左视图）时，它在左视图中是倾斜的实长线，在另外两视图中（即主视图和俯视图）中是垂直于x轴的垂直线（见图2-5c）。

（3）一般位置线段 一般位置线段倾斜于各投影面，因此它在各投影面上的投影均不反映实长，都比原实长短（见图2-6）。

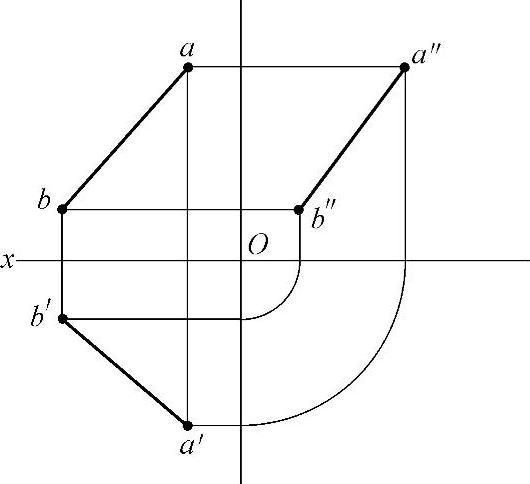
图2-6 一般位置线段在三视图中投影

【小结】

从以上各种线段在视图中的反映，可以得出：

1）线段只有平行投影面在投影面上，才能反映出线段的实长。

2）平行线投影特点。

正平线：线段在主视图中是实长线，在俯视图中是平行于x轴的平行线，在左视图中是垂直于x轴线的垂直线。

水平线：线段在俯视图中是实长线，在其他两视图是平行于x轴的平行线。

侧平线：线段在左视图中是实长线，在其他两视图中是垂直于x轴的垂直线。

2.一般位置线段求实长线的应用

根据线段在三视图中的投影特性（只有当线段平行于投影面时投影面上才能反映实长），我们设法将一般位置线段转换成平行于投影面的正平线、水平线、侧平线，这样就能求出线段的实长。

【例1】 将一般位置线段转换成正平线。

做法如下：

1）做线段ab在一般位置的三视图（见图2-7a）。

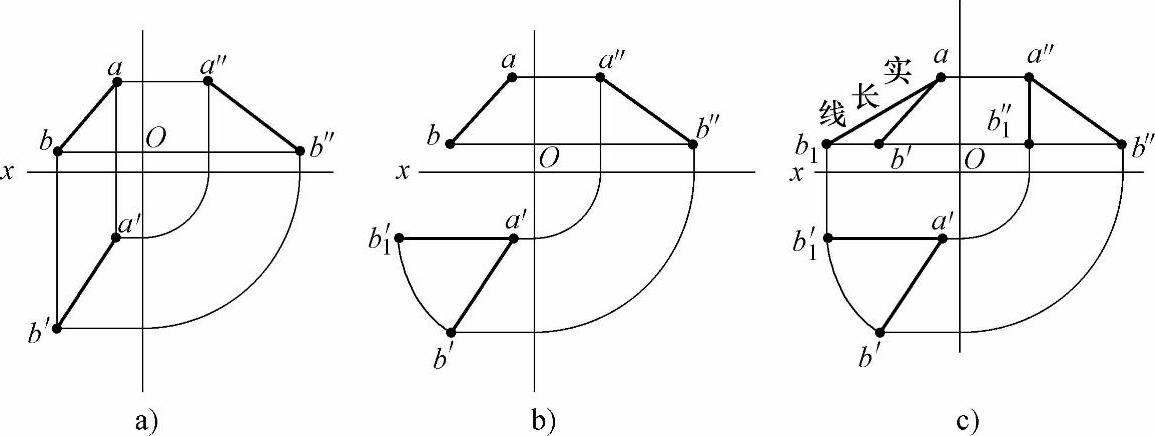
图2-7 一般位置线段转换成正平线

2）在三个视图中分别以a、a′、a″点为定点不动。在俯视图中以a′点为轴，将线段a′b′旋转至与三视图的x轴平行。这样线段a′b′在俯视图中就成为平行于x轴的平行线a′b′₁，线段a′b′就由一般位置变成正平线a′b′₁（见图2-7b）。

3）根据三视图中的投影规律“长对正、高平齐、宽相等”原则，一一对应得左视图和主视图中的b″₁点和b₁点。在主视图上用线段连接a、b₁两点，那么线段ab₁即线段ab的实长线（见图2-7c）。

【例2】 一般位置线段转换成水平线。

做法如下：

1）做线段ab在一般位置的三视图（见图2-8a）。

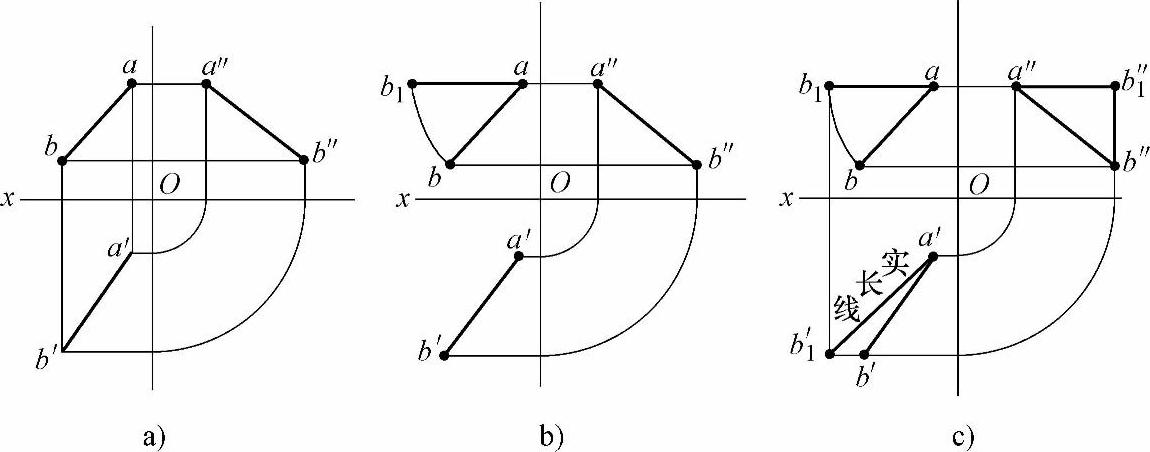
图2-8 一般位置线段转换成水平线

2）在三个视图中分别以a、a′、a″点为定点不动。在主视图中以a点为轴，将线段ab旋转至与三视图的x轴平行。这样线段ab在主视图中就成为平行于x轴的平行线ab₁，线段ab就由一般位置变成水平线ab₁（见图2-8b）。

3）根据三视图中的投影规律“长对正、高平齐、宽相等”原则，一一对应得左视图和俯视图中的b″₁点和b′₁点。在俯视图上用线段连接a′、b′₁两点，那么线段a′b′₁即线段ab的实长线（见图2-8c）。

【例3】 一般位置线段转换成侧平线。

做法如下：

1）做线段ab在一般位置的三视图（见图2-9a）。

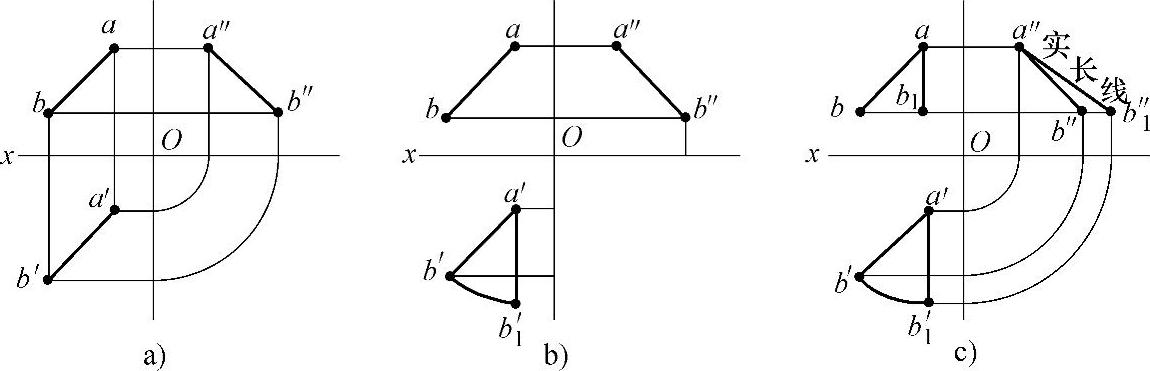
图2-9 一般位置线段转换成侧平线

2）在三个视图中分别以a、a′、a″点为定点不动。在俯视图中以a′点为轴，将线段a′b′旋转至与三视图中的x轴垂直。这样线段a′b′在俯视图中就成为垂直于x轴的垂直线a′b′₁，线段a′b′就由一般位置转换成侧平线a′b′₁（见图2-9b）。

3）根据三视图中的投影规律“长对正、高平齐、宽相等”原则，一一对应得主视图和左视图中的b₁点和b″₁点。在左视图中用线段连接a″、b″₁两点，那么线段a″b″₁即线段ab的实长线（见图2-9c）。

【小结】

从以上三个例子中，我们看到由一般位置线段求实长，可以利用固定线段一端，旋转另一端至平行于x轴或垂直于x轴，使之转换成正平线、水平线、侧平线，重新组成一个新的视图来求得。在这个新视图中，我们看到重新组合的线段有一个特点，那就是可以组成一个直角三角形，旋转至平行于x轴的线段为直角三角形一直角底边，平移后垂直于x轴的线段为另一直角边高，线段的实长就是直角三角形的斜边。

从这个直角三角形求线段实长的方法中可总结出一个规律：三视图中任意一般位置线段，都可以用作图法（直角三角形做图法和计算法）求做出其实长线。

3.直角三角形做图法求实长线的应用

为了做图方便，我们直接可以利用上下两视图（即主视图和俯视图）来求做线段实长，而省去左视图，即不必在图面上再画出左视图。

1）如果在主视图面上求做线段实长，那么俯视图中的线段a′b′就是直角三角形的底边。将主视图中线段下端点b平移至点b₁，使线段ab₁垂直于x轴，则线段ab₁就是直角三角形的一个直角边高（见图2-10a），直角三角形的斜边即为所求实长线（即线段a″b″₁，见图2-10b）。

2）如果在俯视图面上求做线段实长，那么主视图中的线段ab就是直角三角形的底边。将俯视图中线段下端点b′平移至点b′₁，使线段a′b′₁垂直于x轴，则线段a′b′₁就是直角三角形的一个直角边高（见图2-11a），那么直角三角形的斜边即为所求实长线（即线段a″b″₁，见图2-11b）。

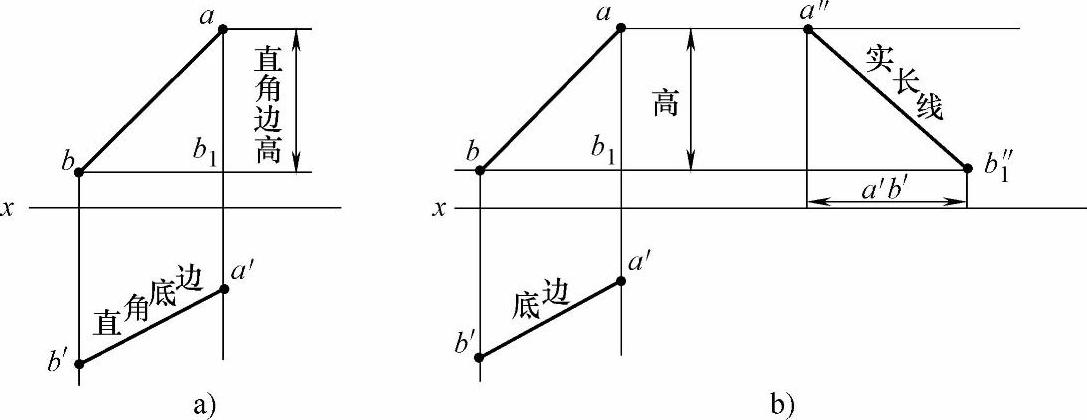
图2-10 主视图面上求线段实长

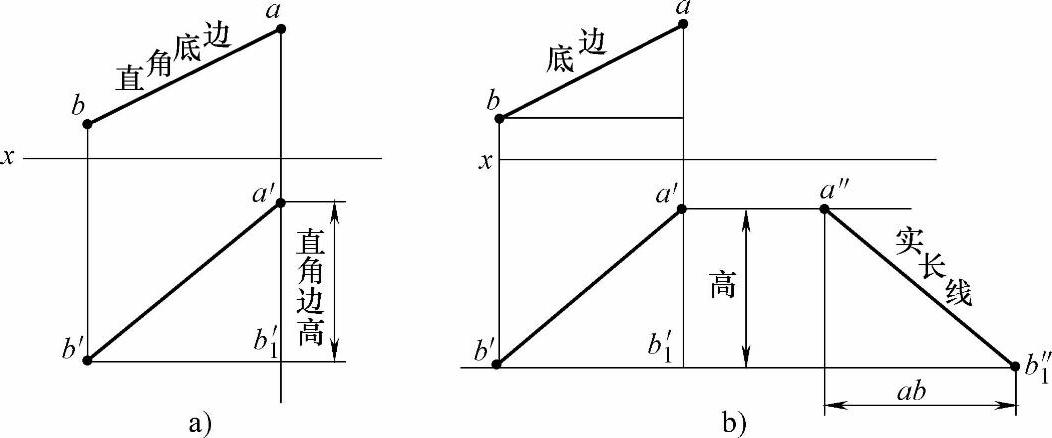
图2-11 俯视图面上求线段实长

我们知道用三角形做图法求线段实长时，直角三角形的斜边即是所求的实长线，所以只需求做出直角边高和直角底边长即可。

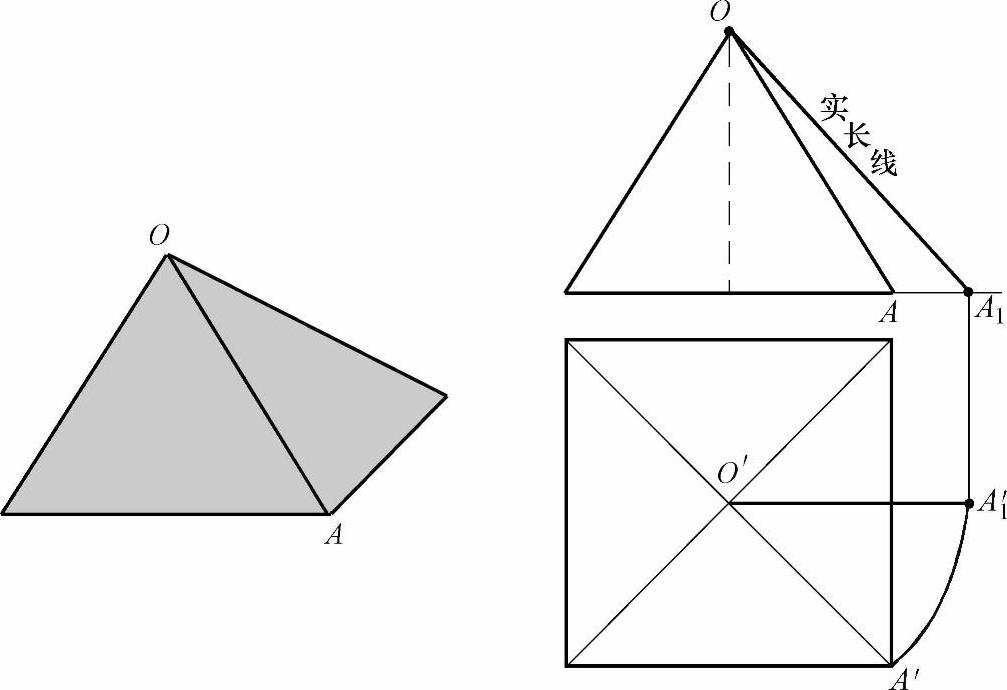
【例4】 求四棱锥棱线实长。

做四棱锥侧面展开图必须先求出棱线实长，在四棱锥的视图中，主、俯两视图中的棱线均不反映实长，所以必须先求出棱线实长后才可做展开。

做法如下：

1）做四棱锥的主、俯两视图，锥顶点为O（俯视图中为O′），锥底一顶点为A（俯视图中为A′）。

2）以俯视图中的O′点为圆心，O′A′为半径画弧，弧线与过O′点平行于x轴的直线交于点A′₁。由A′₁点引上垂线与主视图锥底延长线交于A₁点，主视图中锥底中点至A₁点的长即是直角三角形的底边长，主视图中锥顶O点至锥底中点的长即为直角三角形的直角边高。

3）用线段连接主视图中的O、A₁两点，则线段OA₁即为所求棱线OA的实长（见图2-12）。

(www.xing528.com)

图2-12 求做四棱锥的棱线实长

【例5】 以工厂中常见天圆地方构件为例，来说明直角三角形做图法求线段实长的运用。

视图分析：做天圆地方主、俯两视图，俯视图中四个等腰三角形表示平面部分，各等腰线表示方圆过渡线（平面与曲线的分界线）。这些线在视图中都不反映实长。做展开图时，除需求出这些线的实长外，还需在曲面投影部分做适当数量的辅助线，如俯视图中的线段B′-2′、B′-3′（2′、3′点为1/4圆周的三等分点），同样各辅助线也不反映实长。

实长线求法：求上述各线实长，现场实际放样时多在主视图中做出，为使图面清晰，将实长线画在主视图右侧。主视图中天圆地方的高即为三角形的直角边高，俯视图中的B′-1′、B′-4′、B′-2′、B′-3′都是直角三角形的底边，四条底边线都可做在同一个图面上，即主视图的右侧。因为线段B′-1′和B′-4′的长相等，B′-2′和B′-3′的长相等，所以只需求做出两条实长线即可，即线段B′-1′和B′-2′的实长线。

实长线B′-1′、B′-2′求做步骤：

1）做主视图线段AB向右引的延长线。在线段AB延长线上选一点B″，过B″点向上做延长线的垂线段，垂线段长等于天圆地方的高，得垂线段上端点O″，那么这个垂线段就是直角三角形的一个直角边高。

2）以B″点为圆心，俯视图中线段B′-1′、B′-2′为半径分别画弧，两弧线与线段AB延长线分别交于1″点和2″点，那么1″点和2″点即为三角形斜边的连接点。

3）用线段把O点和1″点、2″点分别相连，相连所得两条线段（即三角形的斜边）就是所求的实长线（见图2-13）。

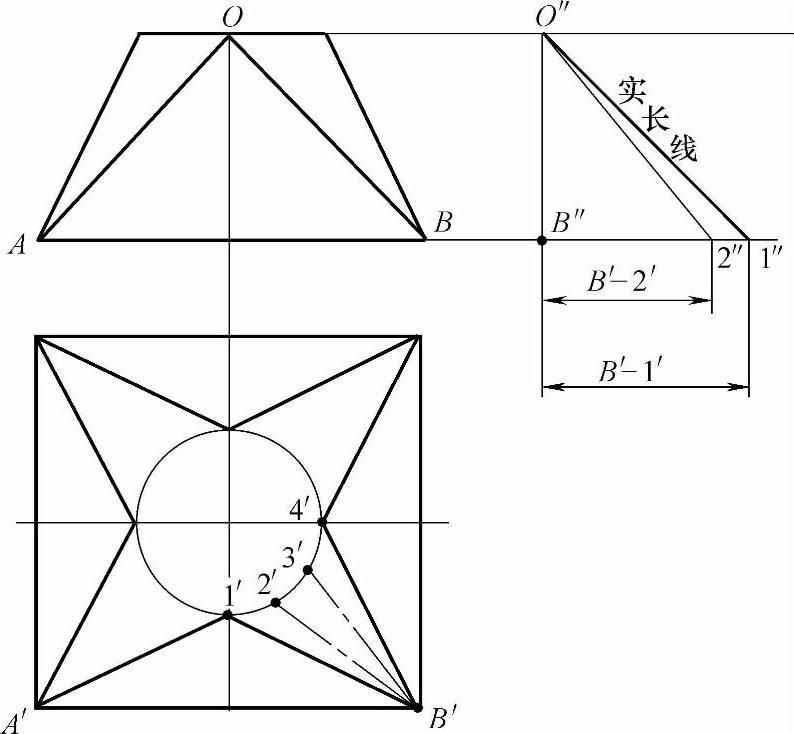
图2-13 求做天圆地方的实长线

4.计算法求实长线的应用

用计算方法求线段实长，省去了在图面上做线段求实长的麻烦，可使图面清晰整洁。

计算法求线段实长的理论根据是直角三角形的勾股定理，即a²+b²=c²（见图2-14）。

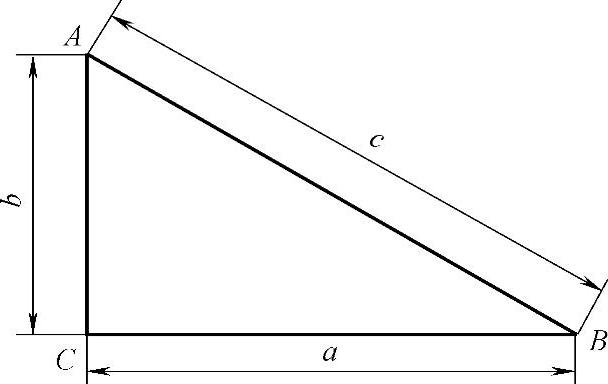
图2-14 直角三角形示意图

从图2-14看到a与b是直角三角形的两条直角边，c是直角三角形的斜边，只要求出两条直角边（即a边与b边），就能求出直角三角形的斜边（即所求线段的实长）。

【例6】 求四棱锥的棱线实长。

视图分析：四棱锥的侧面展开，首先得求出棱锥的棱线实长，而主、俯两视图中棱线均不反映实长，所以必须首先求出才可做展开。

计算法求实长的思路分析：用计算法求线段实长，首先得计算出直角三角形的高和直角底边长，然后才能求出直角的斜边长。这个直角三角形直角边高为已知，即四棱锥在主视图中的高为40（见图2-15），直角底边长即俯视图中线段O′A′的长需要计算求出。求出底边长后就可用勾股定理计算出直角三角形的斜边长，即实长线的长度。

求俯视图中线段O′A′长的计算过程：

（O′A′）2=20²+20²

O′A′=28

棱线实长线即主视图直角三角形的斜边长。

（OA）2=40²+28²

OA=49

因此棱锥的棱线实长为49。

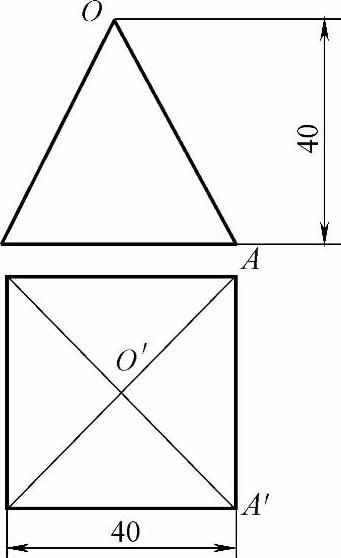
图2-15 四棱锥体主、俯视图

【例7】 求上下口扭成45°方形漏斗的实长线。

视图分析：俯视图中对应连接各角点，分成八个等腰三角形，等腰三角形的边线表示上下口扭转方向后的棱线，这个棱线在主、俯两视图中均不反映实长，在展开之前，需要把棱线实长求出。

计算法求棱线实长的思路分析：用计算法求棱线实长，应用的是勾股定理，所以首先必须求出直角三角形的高和底边长。

计算过程：

直角高为已知，即30（见图2-16），直角底边是俯视图中线段O′A′。

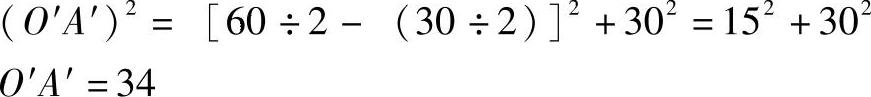
棱线实长即直角三角形斜边长。

（OA）2=34²+30²

OA=45

经过计算棱线实长为45。

图2-16 上下口扭成45°方形漏斗的主、俯视图

5.直角三角形做图法与计算法求线段实长的比较与选择

求线段实长选用何种方法，是用直角三角形做图法还是计算法？这需要根据钣金构件的形状、尺寸、大小及复杂、简易程度而决定。

如果钣金构件较大，所求线段实长比较直观，而尺寸形状要求又比较严格，则宜选用计算法。因为计算法是应用理论计算，可以不在视图面或展开面求线段实长，省去手工在图面上的描画，可使图面保持整洁、清晰。计算法求线段实长是应用平面直角三角形的勾股定理，所以计算出的线段实长精确度高，误差小，计算法宜应用于大型的棱锥构件，如多棱锥的棱线方型漏斗的棱线等。

如果钣金构件较小，所求实长线较多，要求又不太严格，则宜选用直角三角形做图法。因为直角三角形做图法在一个图面上可直接求做出多个实长线，可使所做的实长线与视图上的线段一一对应、一目了然、不易错位。如天圆地方和过渡接头等钣金构件宜选用三角形做图法。

6.结论

实长线的应用非常广泛。我们可以利用实长线的特点，直接用计算法和做图法做出各种构件的棱长、边长、空间曲线实形和实长，以及构件表面的平面实形和构件断面的实形。下面举例说明实长线的应用。

【例8】 求做空间曲线的实形（见图2-17）。

空间曲线在一些视图中往往不反映实形，因此曲线实形或曲线实长求做起来是很困难的。只有把空间曲线扭转成垂直于平行投影面，才能在投影面上反映曲线投影实形。这个扭转过程要多次变换投影面才能达到，投影面的多次变换是很麻烦和费事的，而且在操作过程中还极易出现误差。如果利用线段实长线的特点来做空间曲线的平面实形，则会变得容易、简单和方便，而且做出来的曲线精确度高。

线段实长线求做空间曲线平面实形的过程：

1）按已知条件做出空间曲线主、俯两视图，并在曲线两端点标注A点和B点，曲线中间选一点，标注为C点（见图2-17a）。

2）把主、俯两视图中的A点、B点和C点用线段相连，得三条线段AB、AC和BC，求做出这三条线段的实长（见图2-17b）。

3）做线段AB的实长线，以实长线的一端A点为圆心，线段AC实长为半径画弧，再以实长线另一端的B点为圆心，线段BC实长为半径画弧，两弧交于一点为C点。用虚线把A点至C点，C点至B点相连（见图2-17c）。

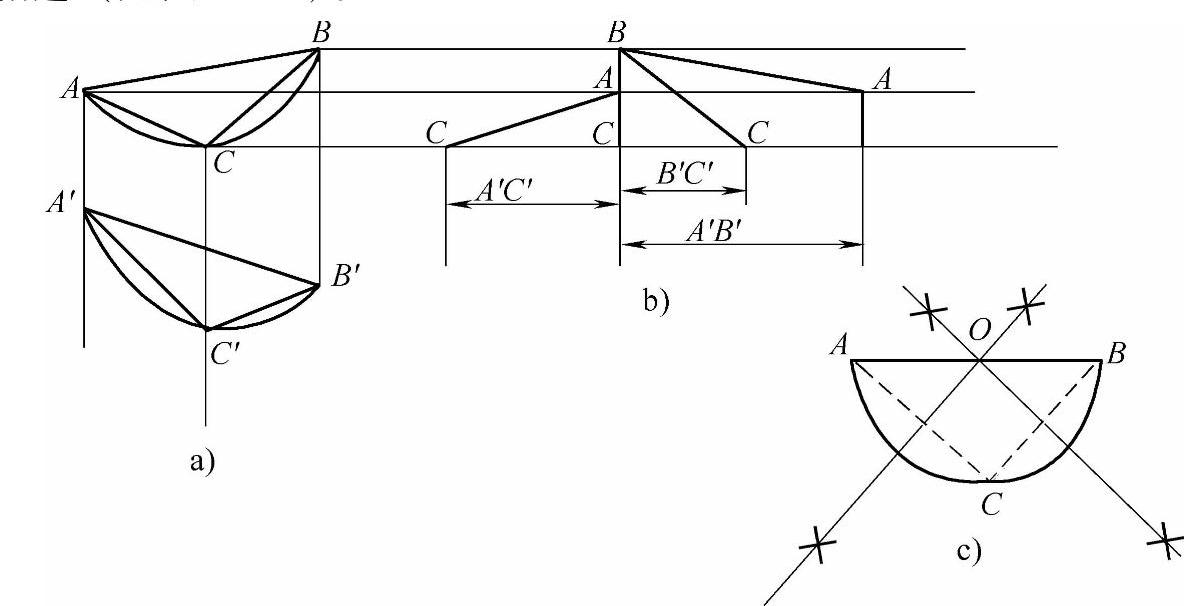
图2-17 求做空间曲线操作过程

4）做虚线线段AC和BC的垂直平分线，两条垂直平分线交于一点为O点。

5）以O点为圆心，O点至A点长为半径画弧。弧线同时经过A点、C点和B点。那么这个所做的弧线就是所求的空间曲线转换成平面曲线的实形。要想求做出这个空间曲线实长，再利用弧线展成直线的做法做出（见第一章第一节“圆弧线展开成大圆弧线或直线的做法”），也可用计算法（查“弧、弦长计算系数表”）。

【例9】 求做一般位置的平面实形。

本例将用两种方法求解：变换投影面和线段实长。

1）变换投影面求三角形平面实形的过程（见图2-18a）：①按已知条件做出三角形的主、俯两视图，并把三个角顶点标注A、B、C点。②从视图中看到三角形的底边BC在主视图中是平行于X轴线的，所以俯视图中的线段BC反映实长。在俯视图下方利用这个线段BC实长做新视图X₁，使X₁轴线垂直于俯视图中的线段BC，俯视图中线段BC向下做延长线，俯视图中的A点向下做垂线垂直于X₁轴线。③量取主视图中A、B、C点与X轴线的距离，把量取完的距离对应搬移到新视图X₁中。在新视图中B点和C点重合，成为一个（B、C）点。做线段把（B、C）点与A点相连。因为三角形在这个视图中是垂直摆放，所以此视图展现为一条直线。④再做一视图X₂，使X₂轴线平行于上一视图X₁的三角形（B、C）A直线。过X₁视图上的（B、C）点和A点向下做垂线垂直于X₂轴线，量取俯视图中三角形A、B、C三点与X₁轴线的距离，对应搬移到新视图X₂上的各条垂线上，得交点为A、B、C三点。用线段把这三个点分别相连，相连后的图形即是所求三角形的平面实形。

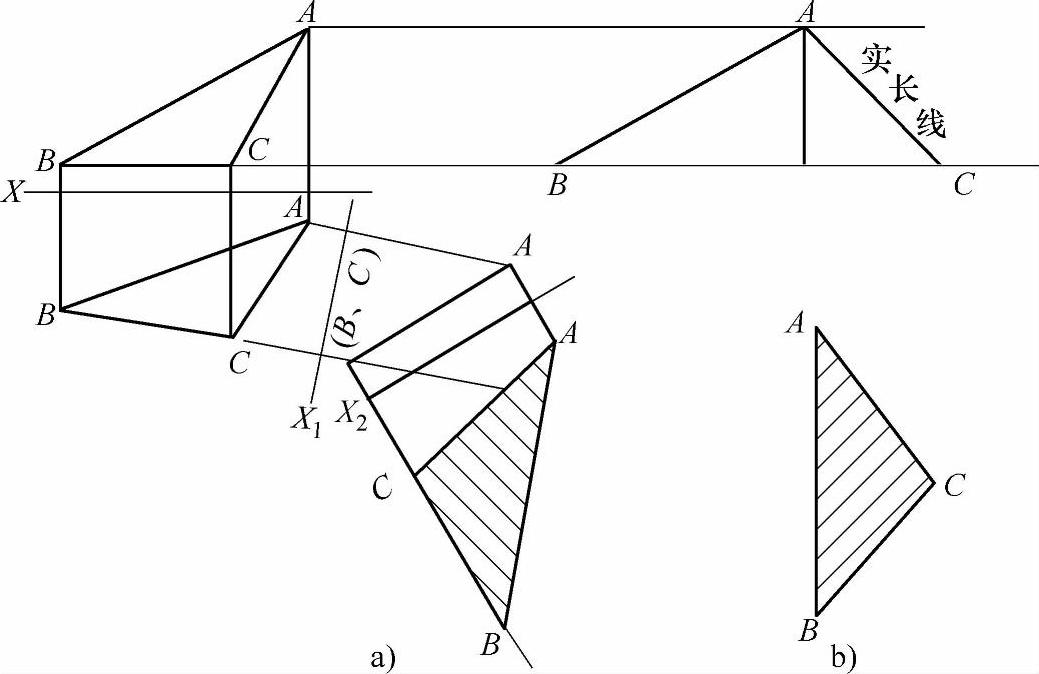
图2-18 求做一个三角形的平面实形两种方法操作过程

a）变换投影法 b）线段实长线法

2）线段实长线求三角形平面实形过程（见图2-18b，三角形为三条边所构成，所以必须求出三条边的实长才可以做出这个三角形的平面实形）：①因为主视图中线段BC平行于X轴线，所以俯视图中的线段BC反映实长，不必再求做。只需求做出三角形另外两条边线的实长，即AB和AC即可。用做图法在主视图右边做出线段AB和AC的实长。②做线段AB实长线。以实长线的一端A点为圆心，线段AC实长线长为半径画弧，再以实长线B点为圆心，线段BC实长线长为半径画弧，两弧交于一点为C点。用线段把A点至C点、B点至C点相连。相连后的图形即是所求的三角形平面实形。

【例10】 求做四棱锥体被斜切的截平面实形（见图2-19）。

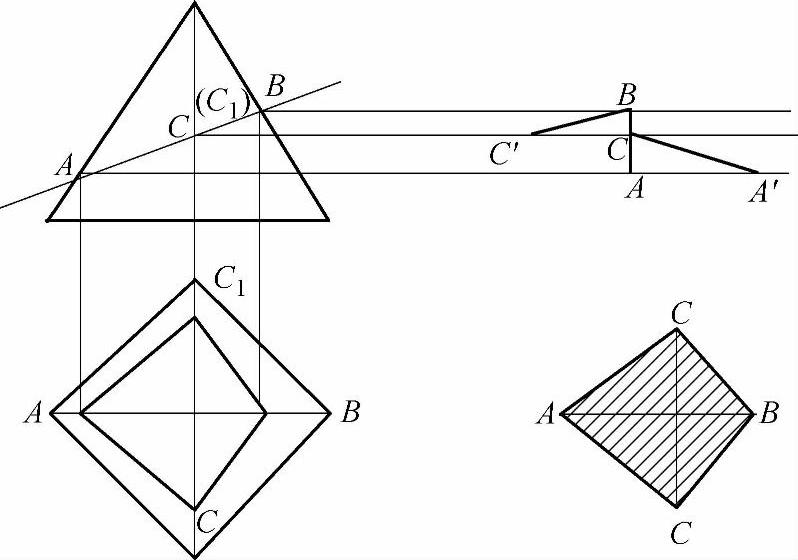
图2-19 四棱锥体被斜切的截平面

1）按已知条件做出四棱锥体斜切截平面的主、俯两视图，并在斜切四棱锥棱线切点处标注A、C、B、C′点。

2）四棱锥被斜切的截平面从俯视图中看到是一个四边形，四条边为四条线段，即线段AC、AC′、BC、BC′。因为线段AC和AC′相等，BC和BC′相等，所以只需求做出两条线段实长即可。在主视图右边做出AC和BC线段的实长。

3）斜切线段AB在俯视图中平行于X轴线，所以主视图中的线段AB反映实长。

4）在适宜地方做线段AB。以A点为圆心，线段AC实长线长为半径画弧，再以B点为圆心，线段BC实长线长为半径向两边画弧。弧线与弧线相交，得到两个交点，即C点和C₁点。用线段把A点至C点，C点至B点、B点至C₁点，C₁至A点相连。相连后的图形即是四棱锥体被斜切后的截平面实形。

从以上三个例子中可以看到，用线段实长法去求做各种图形方便、简单、容易、快捷，而且做出的图形准确度也大大提高了。