椭圆轮廓加工技巧

1.定义

椭圆是平面上到两定点的距离之和为常值的点的轨迹，也可定义为到定点距离与到定直线间距离之比为常值的点的轨迹，如图5-10所示。

2.椭圆方程

1）椭圆的标准方程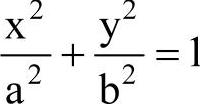，其中b²=a²-c²，满足a＞b＞0。

2）椭圆的参数方程：

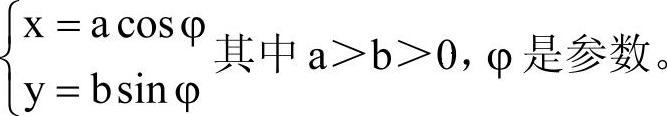
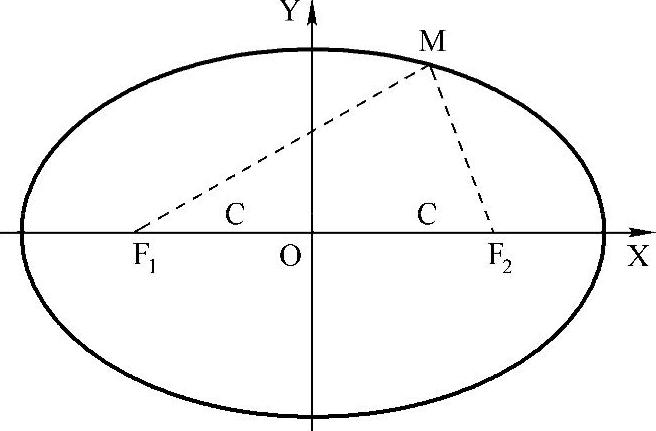
图5-10 椭圆

3.范围

由椭圆的标准方程知，椭圆上点的坐标（x，y）都适合不等式x²/a²≤1，y²/b²≤1，说明椭圆位于直线x=±a和直线y=±b所围成的矩形里。

4.对称性

在椭圆的标准方程中，把x换成-x，或把y换成-y，或把x、y同时换成-x、-y时，方程都不变，所以图形关于Y轴、X轴或原点对称。这时，坐标轴是椭圆的对称轴，原点是椭圆的对称中心。

5.顶点

在椭圆的标准方程中，令x=0，得y=±b，点B₁（0，-b）、B₂（0，b）是椭圆和Y轴的两个交点；令y=0，得x=±a，点A₁（-a，0）、A₂（a，0）是椭圆和X轴的两个交点。Y轴、X轴是椭圆的对称轴，椭圆与Y轴、X轴有四个顶点A₁（-a，0）、A₂（a，0）、B₁（0，-b）、B₂（0，b），这四个点即是椭圆的顶点。

线段A₁A₂、B₁B2分别叫做椭圆的长轴、短轴。它们的长分别等于2a和2b，a和b分别叫做椭圆的长半轴长和短半轴长。

6.离心率

椭圆焦距与长轴长之比e=c/a，叫做椭圆的离心率。因为a＞b＞0，所以0＜e＜1。e越接近1，则c越接近a，从而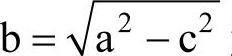越小，因而椭圆越扁；反之，e越接近0，则b越接近a，这时椭圆就接近于圆。

如果a=b，则c=0，两个焦点重合，这时椭圆的标准方程为

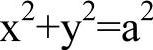
椭圆就变成圆。

7.椭圆标准方程及性质（表5-3）

表5-3 椭圆标准方程及性质

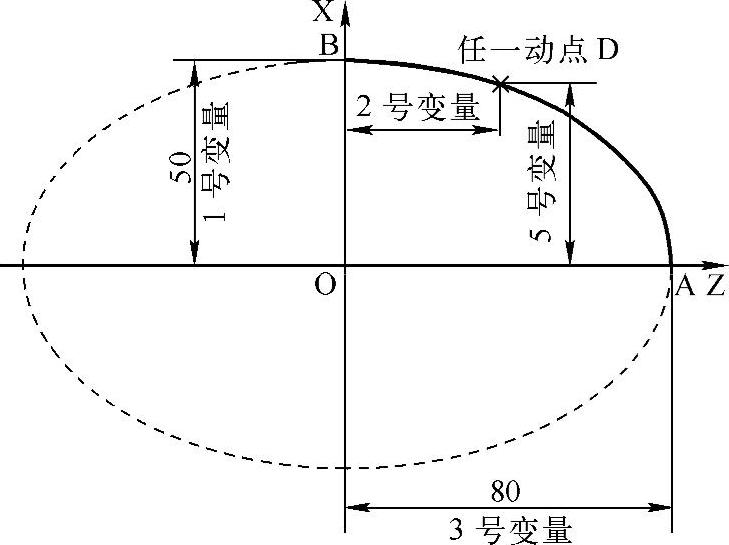
图5-11 椭圆曲线零件示意图

8.构建宏程序

如图5-11所示，编制一个车削加工右1/2椭圆零件的回转轮廓线程序，椭圆方程为x²/a²+z²/b²=1，使用变量编制零件加工的宏程序。

工艺分析 以单层宏程序为例，欲车削图5-11所示x²/a²+z²/b²=1椭圆的回转零件时，在数控程序中用任意一点D的z值（用2号变量）来表达该点的x值（用5号变量）；根据椭圆方程：x²/a²+z²/b²=1得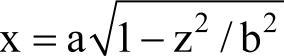，加工从A（x=0，z=b）点到B（x=a，z=0）点，z值从b到0以一定值递减，相应地x值从0到a按计算公式递增。编程中首先采用直线逼近零件轮廓节点的方法，即在Z方向分段。为保证零件的加工精度，以0.1为一个步距，并把Z作为自变量，X作为Z的函数，利用椭圆方程求出其上各点的坐标，然后把各点连接在一起最终形成椭圆。为了适应不同的椭圆，可以编制一个只有变量不用具体数据的宏程序，然后在主程序中调用该宏程序的用户宏指令为上述变量赋值。这样只需要修改主程序中用户宏指令段内的赋值数据就可以直接进行加工。

采用用户宏指令调用加工零件。

（1）参数说明

#1；（A）椭圆短轴半径

#2；（B）椭圆上任意一点Z坐标值

#3；（C）椭圆长轴半径

#5；（J）椭圆上任意一点X坐标值

#6；（K）Z坐标值每次变化量1

#7；（D）0(www.xing528.com)

#8；进给速度

（2）主程序

O0001；

（3）用户宏程序

O0002；

9.宏程序实例

加工图5-12中椭圆部分，编制一个车削加工带椭圆零件的程序，椭圆方程为x²/22²+z²/25²=1，使用变量编制该零件加工的宏程序。

（1）编程工艺设计

以工件右端面建立工件坐标系（编程坐标系与工件坐标系重合），以椭圆的直径取适当倍数为毛坯值，根据工件材料、刀具等要素确定背吃刀量，椭圆短轴直径为比较值，建立分层循环（图5-13）。以椭圆任一动点的Z坐标为自变量，X为应变量，利用椭圆公式完成单层椭圆的加工。加工过程中，以前一刀加工时的短轴直径减背吃刀量与椭圆的实际短轴直径相比较构成分层循环，大于、等于椭圆的实际短轴直径时分层切削。由于先运算后比较存在欠切现象，则判断小于椭圆的实际短轴直径减背吃刀量时，以椭圆的实际短轴直径赋值，完成椭圆加工，避免欠切现象。

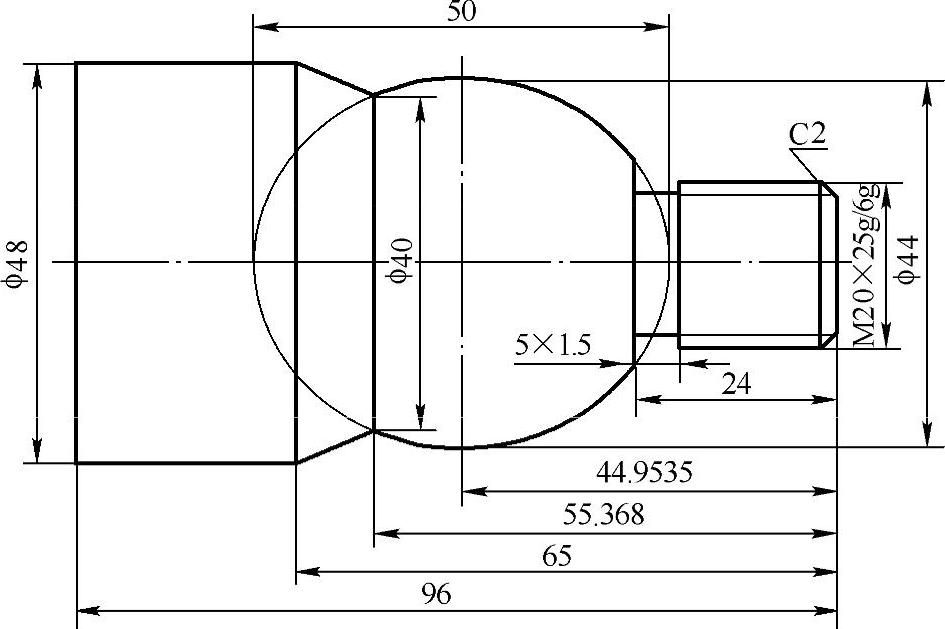
图5-12 椭圆轮廓零件编程实例图

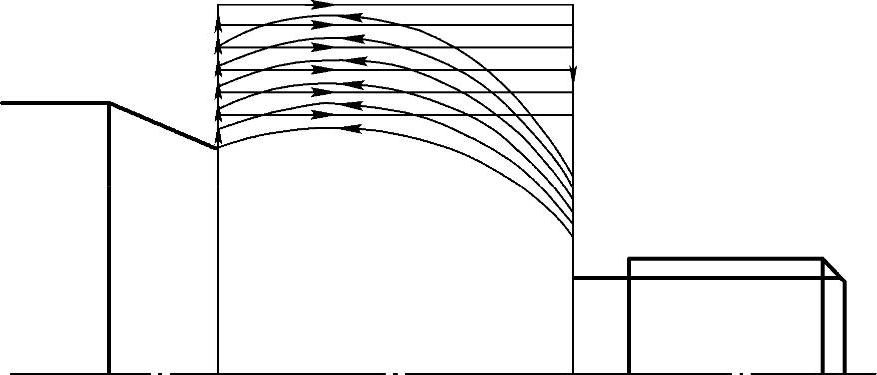
图5-13 椭圆轮廓加工刀具轨迹图

（2）加工参考程序

1）参数说明：

#1；椭圆任一动点的X直径值

#2；椭圆任一动点的Z值，动点距椭圆坐标系原点Z向距离

#3；椭圆加工时短轴赋值

#4；椭圆长半轴

#5；椭圆坐标系原点与工件坐标系原点的距离

#6；步距（自变量Z轴方向上的增量）

#7；椭圆任一动点Z向的终点，动点距椭圆坐标系原点Z向距离

#8；X方向上的背吃刀量

#9；椭圆短轴直径

#10；椭圆Z向起刀点与工件坐标系原点的距离

2）主程序：

O9501；

3）用户宏程序：

O9502；