双曲线轮廓加工技术优化方案

图5-4 双曲线

1.定义

1）第一定义：平面内到两定点F₁、F₂的距离之差的绝对值等于定长2a（小于|F₁F₂|）的点的轨迹叫双曲线，如图5-4所示。

说明：

①||PF₁|-|PF₂||=2a（2a＜|F₁F₂|）是双曲线；若2a=|F₁F₂|，轨迹是以F₁、F₂为端点的射线；2a＞|F₁F₂|时无轨迹。

②设M是双曲线上任意一点，若M点在双曲线右边一支上，则|MF₁|＞|MF₂|，|MF₁|-|MF₂|=2a；若M在双曲线的左支上，则|MF₁|＜|MF₂|，|MF₁|-|MF₂|=-2a，故|MF₁|-|MF₂|=±2a，这是与椭圆不同的地方。

2）第二定义：平面内动点到定点F的距离与到定直线L的距离之比是常数e（e＞1）的点的轨迹叫双曲线，定点叫焦点，定直线L叫相应的准线。

2.范围

双曲线在不等式x≥a和x≤-a所表示的区域内。

3.对称性

以-y代y，方程不变，所以双曲线关于X轴对称；以-x代x，方程不变，所以双曲线关于Y轴对称；同时以-y代y，以-x代x，方程不变，所以双曲线关于原点对称。

4.顶点

令y=0，得x=±a，因此双曲线和它的一条对称轴——X轴有两个交点A₁（-a，0），A₂（a，0）。

令x=0时，解得y²=-b²，无实数解，说明双曲线与它的另一条对称轴——Y轴没有交点。

故双曲线和它的对称轴有两个交点A₁（-a，0）、A₂（a，0），它们叫做双曲线的顶点。

线段A₁A₂叫双曲线的实轴，它的长等于2a，a叫做双曲线的实半轴长；线段B₁B₂叫做双曲线的虚轴，它的长等于2b，b叫做双曲线的虚半轴长。

5.渐进线

1）把两条直线叫做双曲线的渐进线；

2）从图5-4可以看出，双曲线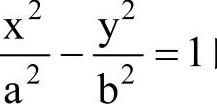的各支向外延伸时，与直线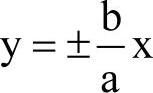逐渐接近。

6.离心率

双曲线的焦距与实轴长的比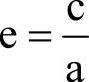，叫双曲线的离心率，。

7.双曲线标准方程及性质（表5-1）

表5-1 双曲线标准方程及性质

（续）

8.几个概念

（1）等轴双曲线实、虚轴相等的双曲线。等轴双曲线的渐近线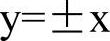为，离心率为。

（2）共轭双曲线

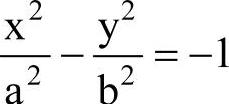以已知双曲线的实轴为虚轴，虚轴为实轴的双曲线叫原双曲线的共轭双曲线，例：的共轭双曲线是。(www.xing528.com)

1）双曲线及其共轭双曲线有共同的渐近线。但有共同渐近线的两双曲线不一定是共轭双曲线。

2）双曲线和它的共轭双曲线的四个焦点在同一个圆周上。

9.构建宏程序

如图5-5所示，编制一个车削加工带双曲线零件的程序，过渡双曲线方程为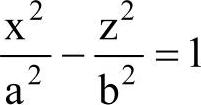，双曲线实半轴长为a，虚半轴长为b，使用变量编制零件加工的宏程序。

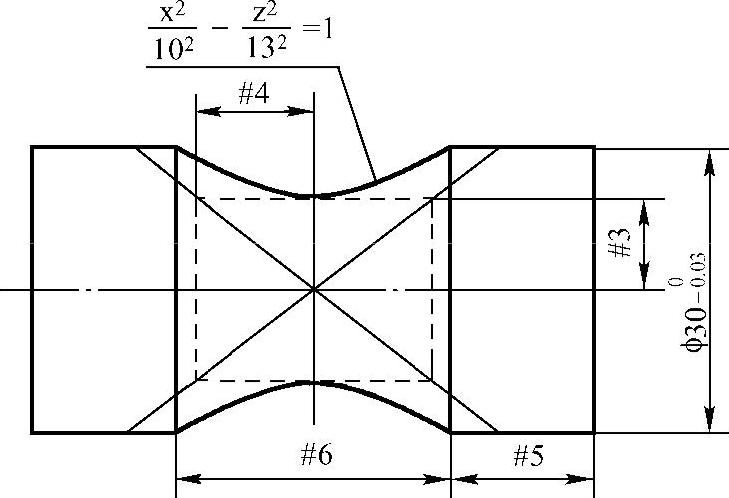
图5-5 双曲线零件示意图

工艺分析 车削图5-5所示双曲线过渡的回转零件时，由于BEIJINGFANUC 0i-TC系统只能实现工件坐标原点Z向偏置，故编程中首先采用直线逼近零件轮廓节点的方法，即在Z方向分段。为保证零件的加工精度，以0.1为一个步距，并把Z作为自变量，X作为Z的函数，利用双曲线方程求出其上各点的坐标，然后利用数学计算使其偏移到相应位置，并把各点连接在一起最终形成双曲线。为了适应不同的双曲线，可以编制一个只有变量不用具体数据的宏程序，然后在主程序中调用该宏程序的用户宏指令为上述变量赋值。这样，对于不同的双曲线，只需要修改主程序中用户宏指令段内的赋值数据就可以进行加工。

采用用户宏指令调用加工零件。

（1）参数说明

#1；双曲线任一动点X方向的坐标值

#2；双曲线任一动点Z方向的坐标值

#3；双曲线实半轴长

#4；双曲线虚半轴长

#5；双曲线起点在工件坐标系里Z轴上坐标值的绝对值

#6；双曲线的开口距离

#7；X方向的步距值

#8；进给速度

（2）主程序

10.宏程序实例

编制一个车削加工带双曲线零件的程序（图5-6），双曲线方程为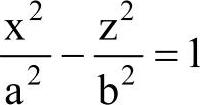，双曲线的开口距离为29.07mm，使用变量编制该零件加工的宏程序。

（1）编程工艺设计

以工件右端面建立工件坐标系（编程坐标系与工件坐标系重合），以圆弧替代双曲线方程，利用系统提供的外圆加工循环及精加工循环对零件进行粗、精加工，然后再对双曲线轮廓进行精加工。编程中采用直线逼近零件轮廓节点的方法，即在Z方向分段。为保证零件的加工精度，以0.1为一个步距，并把Z作为自变量，X作为Z的函数，利用双曲线方程求出其上各点的坐标，然后把各点连接在一起最终形成抛物线。

图5-6 双曲线轮廓零件编程实例图

（2）加工参考程序

子程序：