数控编程中的数学处理方法

编程时的数学处理，都要按零件图样、已确定的加工路线和允许的编程误差，计算出工件加工时的轨迹尺寸，即计算工件轮廓的基点或节点的坐标。对不具备刀具补偿功能的数控系统，还需计算刀具中心（刀位点）轨迹的基点和节点的坐标。

零件的轮廓一般都由许多不同的几何元素构成，如直线、圆弧、椭圆、双曲线及一般的二次曲线等，各几何元素的连接点称为基点，如相邻两直线的交点、直线与圆弧的交点或切点等。对于轮廓形状简单的零件，由于数控系统一般具有直线、圆弧插补和刀具补偿功能，数学处理只需计算零件轮廓上的基点坐标值。当零件形状复杂或零件形状与机床数控系统的插补功能不一致时，计算就比较复杂，必须用若干直线段来逼近这类曲线。要将轮廓曲线分段，用一段段直线或圆弧逼近，逼近线段与非圆曲线的交点称为节点，此时数学处理的任务是计算出各个分隔点的坐标值，并使逼近误差小于允许值。根据这些节点坐标，才能编写出轮廓曲线的加工程序。

对于没有数学方程表达式的列表曲线，如果数据点给的比较密集，则可利用这些点作为节点，用直线或圆弧连接来逼近轮廓形状。数据点比较稀疏时，通常先用插值法将节点加密或进行曲线拟合，然后再进行曲线逼近。对于空间曲面，实际是用许多的平行平面的曲线来逼近空间曲面，这时需求出所有的平面曲线，并计算各平面曲线的基点或节点，然后编写各基点、节点之间的直线或圆弧加工程序。

当采用CAD/CAM软件自动编程时，这些数学处理由计算机进行。

数控机床一般都具有直线插补和圆弧插补的功能，因此对于由直线、圆弧组成的平面轮廓零件，它的数值计算比较简单，主要是基点的计算。基点坐标的计算一般比较简单，可根据零件图样给定的尺寸，运用代数、几何、三角、解析几何的有关知识，直接计算出数值。

数控系统一般都只有直线和圆弧插补功能，这种机床无法直接加工除直线和圆弧以外的曲线，如渐开线、椭圆、双曲线、阿基米德螺旋线、抛物线等。对于这些非圆曲线轮廓，只有用直线或圆弧去逼近它，即将轮廓曲线按编程允许的误差分割成许多小段，再用直线或圆弧去逼近这些小段。逼近线段与非圆曲线的交点或切点称为节点，对这种轮廓进行数学计算，实质就是计算各节点的坐标。

1.用直线逼近零件轮廓的节点计算

（1）等间距法

等间距法是最简单的一种方法，这种方法是使每个程序段的某一坐标增量相等，然后根据曲线的表达式求出各节点的坐标值。如图5-1所示，将曲线y=f（x）的X轴分成等间距，然后由起点开始，每次增加一个坐标增量值（间距），根据给定的Δx求出x_i，将x_i代入y=f（x）即可求出另一个坐标值y_i，这样依次类推，直至求出曲线上所有相应节点的x、y坐标值，并以该坐标值编制直线段程序。

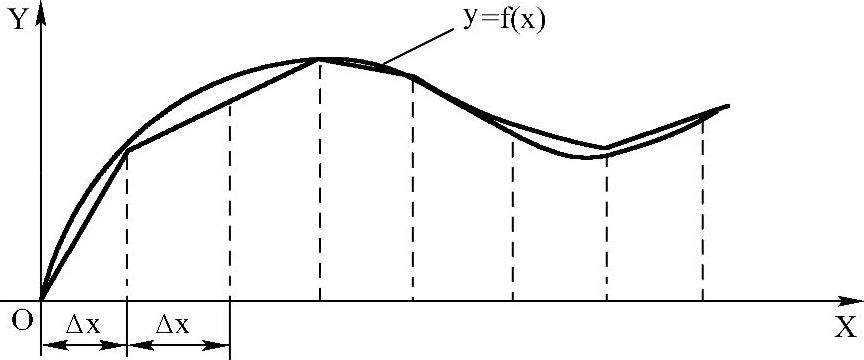
图5-1 等间距直线逼近求节点

这种方法的关键是确定间距值，该值应保证曲线y=f（x）相邻两节点连线间的法向距离小于允许的程序编制误差。在实际生产中，根据零件加工精度要求凭经验选取间距值。由于间距值Δx应保证曲线曲率最大处的逼近误差小于允许值，所以程序可能过多。

（2）等弦长法

这种方法是使所有逼近线段的弦长相等，如图5-2所示。由于零件轮廓曲线的曲率各处不等，因此各程序段的程序编制误差δ也不等，这就要使各程序段的最大误差δ_max小于允许误差δ允，才能满足程序编制的精度要求。在用直线逼近曲线时，可以认为误差的方向是在曲线y=f（x）的法向，同时误差最大值发生在曲率半径最小处。

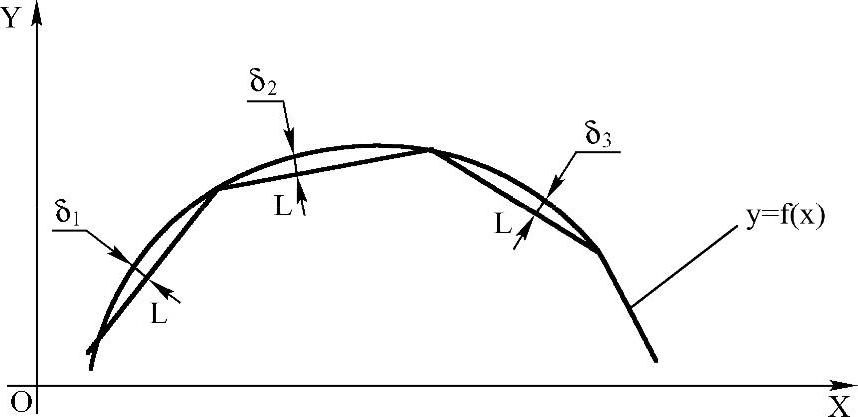
图5-2 等弦长直线逼近求节点(https://www.xing528.com)

等弦长法数学处理的步骤如下：

1）确定允许的弦长L。由于最大误差必在曲率半径最小处，因此先确定曲率半径最小处，然后在该处按逼近误差小于或等于允许误差δ_允的条件求出允许的弦长L，弦长。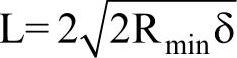

2）用弦长分割轮廓曲线。以曲线起点A为圆心，作半径L的圆交曲线y=f（x）于B点，求出B点的坐标。

3）依次以B、C、D、…为圆心，可求出其余各点的坐标值。

（3）等误差法

等误差法是以直线拟合轮廓曲线时使所有逼近线段的误差δ相等，并且小于或等于允许误差，如图5-3所示。用这种方法确定的各逼近线段长度不等，逼近线段数目较少，但其计算过程比较复杂，要由计算机辅助完成，算法也较多，而且还在发展中。

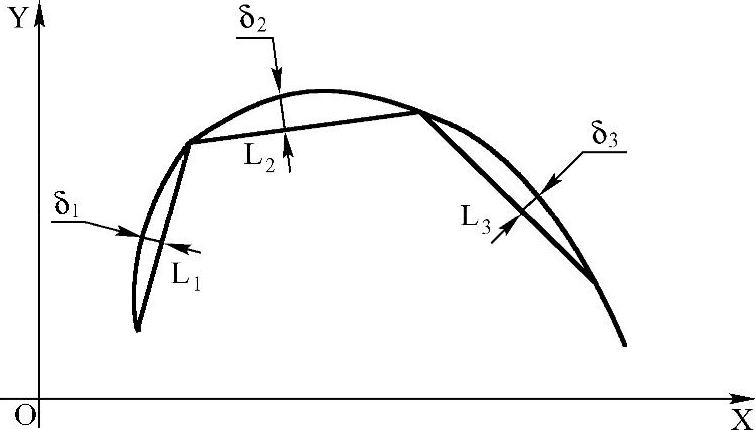
图5-3 等误差法直线逼近求节点

2.用圆弧逼近零件轮廓的节点计算

轮廓曲线y=f（x）也可以用圆弧来逼近，并使逼近误差小于或等于允许误差。用圆弧逼近法去逼近零件的轮廓曲线时，需求出每段圆弧的圆心、起点和终点的坐标，以及圆弧的半径。

用圆弧逼近曲线的方法有曲率圆法、三点作圆法、相切圆法等。其中，三点作圆法、相切圆法都要先用直线逼近方法求出各节点，再通过已知节点求出圆，计算较烦琐。三点作圆法是通过已知的三个节点求圆，并作为一个圆弧插补程序段；相切圆法是通过已知的四个节点分别作出两个相切的圆，编出两个插补程序段，这种方法逼近轮廓的相邻各圆弧是相切的；曲率圆法是一种等误差圆弧逼近法。

3.列表曲线平面轮廓的数学处理方法

列表曲线是指已经给出曲线上某些坐标，但没有给出方程，机械加工中很多轮廓曲线是用这种离散的列表点来描述的。当给出的列表曲线已密到不影响曲线的精度时，可直接在相邻列表点间用直线段或圆弧段编程，但实际上往往给出的只是很少几点，为保证精度，就要增加新的节点（也称插值）。

处理列表曲线的一般方法是采用二次拟合法，即先根据已知列表点导出插值方程（第一次曲线拟合），用数学方程式逼近列表曲线；然后再根据插值方程进行插值点加密求得新的节点（用直线段或圆弧段来逼近插值方程曲线，称二次拟合），从而编制逼近线段的程序。