算术和逻辑运算指令详解：FANUC 0i控制系统

表3-13中列出的运算可以在变量中运行。等式右边的表达式可包含常量或由函数、运算符组成的变量。表达式中的变量#j和#k可以用常量赋值。等式左边的变量也可以用表达式赋值。其中算术运算主要是指加、减、乘、除、函数等，逻辑运算可以理解为比较运算。

表3-13 FANUC 0i算术和逻辑运算

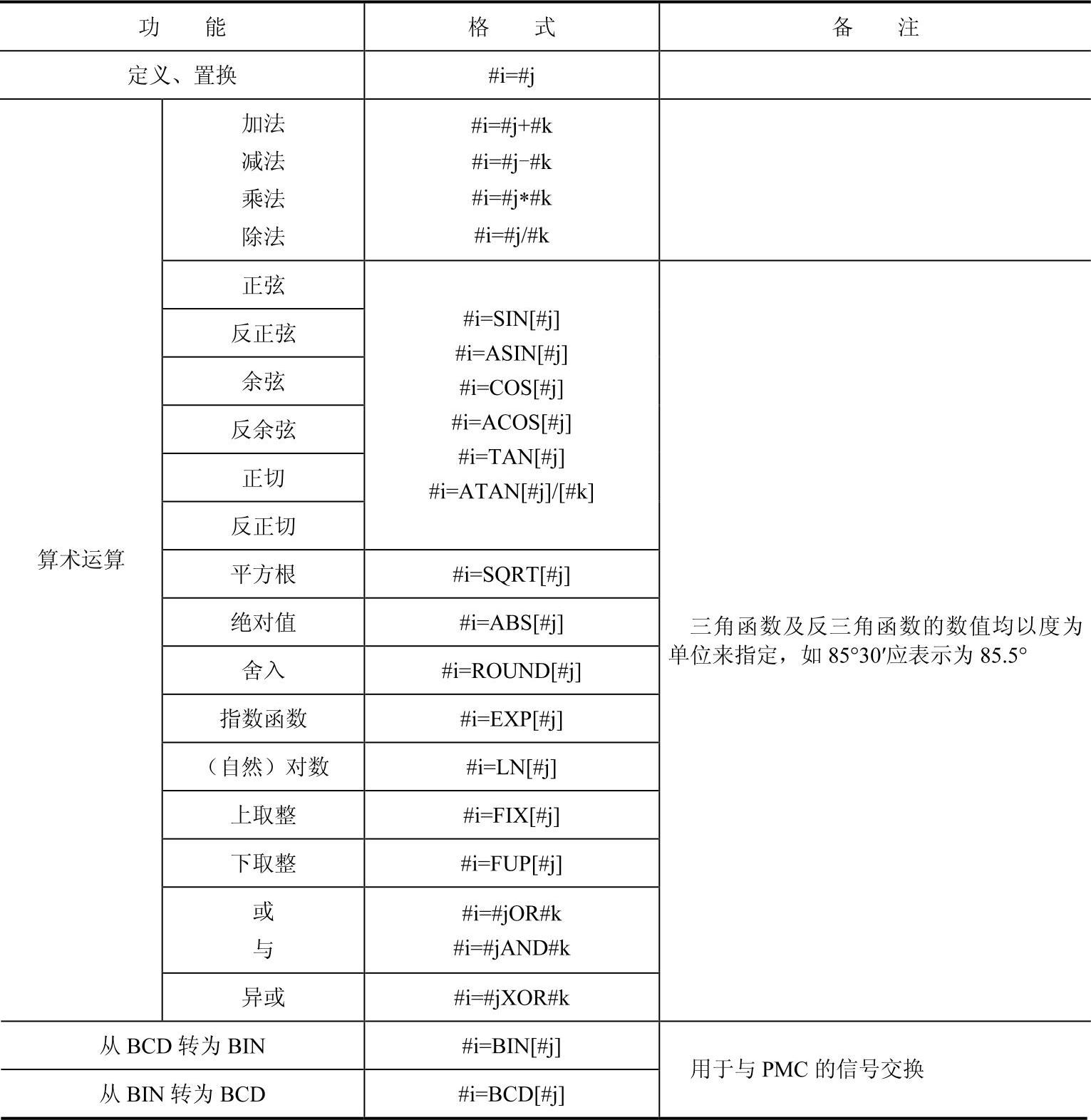
以下是算术和逻辑运算指令的详细说明。

1.反正弦运算#i=ASIN[#j]

1）取值范围如下：

当参数（No.6004#0）NAT位设置为0时，在90°～270°范围内取值。

当参数（No.6004#0）NAT位设置为1时，在-90°～90°范围内取值。

2）当#j超出-1到1的范围时，触发程序错误P/S报警No.111。

3）常数可替代变量#j。

2.反余弦运算#i=ACOS[#j]

1）取值范围：0°～180°。

2）当#j超出-1到1的范围时，触发程序错误P/S报警No.111。

3）常数可替代变量#j

3.反正切运算#i=ATAN[#i]/[#k]

1）采用比值的书写方式（可理解为对边/邻边）。

2）取值范围如下：

当参数（No.6004#0）NAT位设置为0时，取值范围为0°～360°。例如，当指定#1=ATAN[-1]/[-1]时，#1=225°。

当参数（No.6004#0）NAT位设置为1时，取值范围为-180°～180°。例如，当指定#1=ATAN[-1]/[-1]时，#1=-135。

3）常数可替代变量#j。

4.自然对数运算#i=LN[#j]

1）相对误差可能大于10^-8。

2）当反对数（#j）为0或小于0时，触发程序错误P/S报警No.111。

3）常数可替代变量#j。

5.指数函数#i=EXP[#j]

1）相对误差可能大于10^-8。

2）当运算结果超过3.65×10⁴⁷（j大约是110）时，出现溢出并触发程序错误P/S报警No.111。

3）常数可替代变量#j。

6.上取整#i=FIX[#j]和下取整#i=FUP[#j]

CNC处理数值运算时，无条件地舍去小数部分称为上取整；小数部分进位到整数称为下取整（注意与数学上的四舍五入对照）。对于负数的处理要特别小心。

例如：假设#1=1.2，#2=-1.2。

1）当执行#3=FUP[#1]时，2.0赋予#3。

2）当执行#3=FIX[#1]时，1.0赋予#3。

3）当执行#3=FUP[#2]时，-2.0赋予#3。

4）当执行#3=FIX[#2]时，-1.0赋予#3。

7.算术与逻辑运算指令的缩写(www.xing528.com)

程序中指令函数时，函数名的前两个字符可以用于指定该函数。

例如：ROUND→RO FIX→FI

8.混合运算时的运算顺序

上述运算和函数可以混合运算，即涉及运算的优先级，其运算顺序与一般数学上的定义基本一致，优先级顺序从高到低依次为：

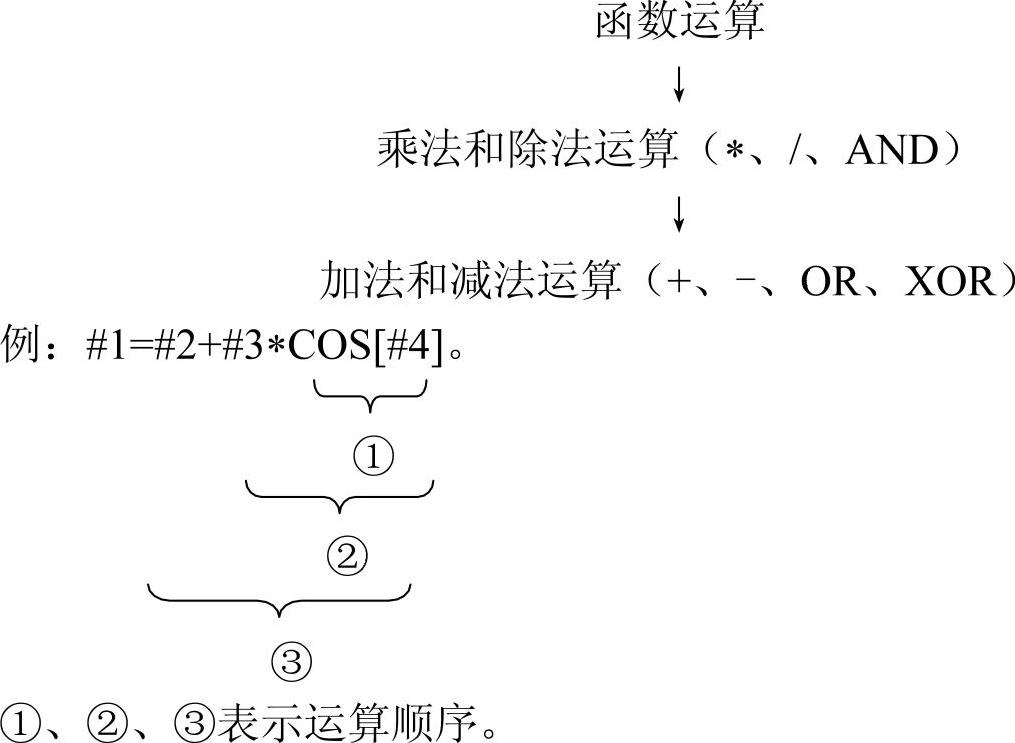
9.括号嵌套

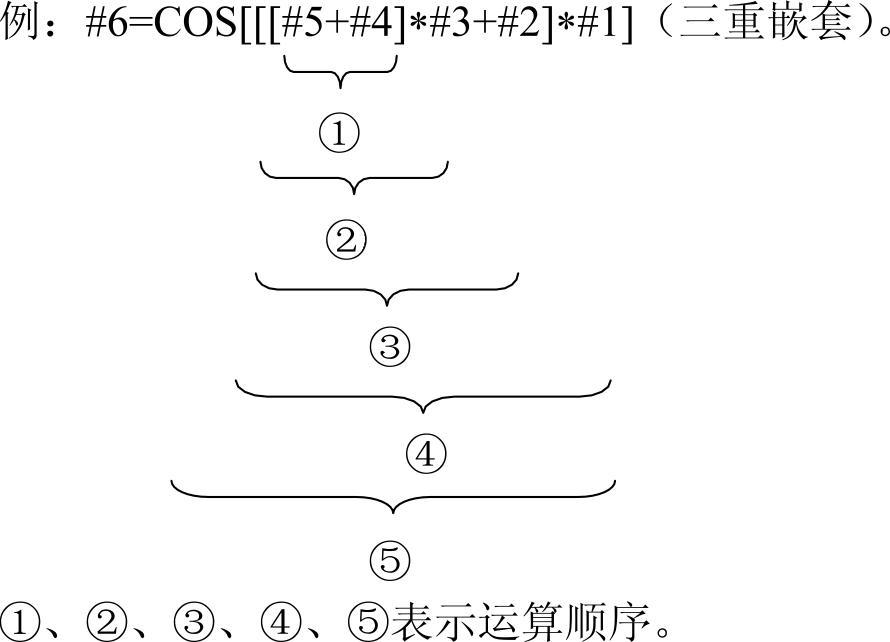
用“[]”可以改变运算顺序，最里层的[]优先运算。括号[]最多可以嵌套5级（包括函数内部使用的括号）。当超出5级时，触发程序错误P/S报警No.118。

10.逻辑运算说明

逻辑运算相对于算术运算来说，更为特殊和费解，详细说明见表3-14。

表3-14 FANUC 0i逻辑运算说明

11.运算精度

同任何数学计算一样，运算的误差是不可避免的，用宏程序运算时必须考虑用户宏程序的精度。用户宏程序处理数据的浮点格式为：M×2^E。

每执行一次运算，便产生一次误差，在重复计算的过程中，这些误差将累加。FANUC 0i运算中的误差见表3-15。

表3-15 FANUC 0i运算中的误差

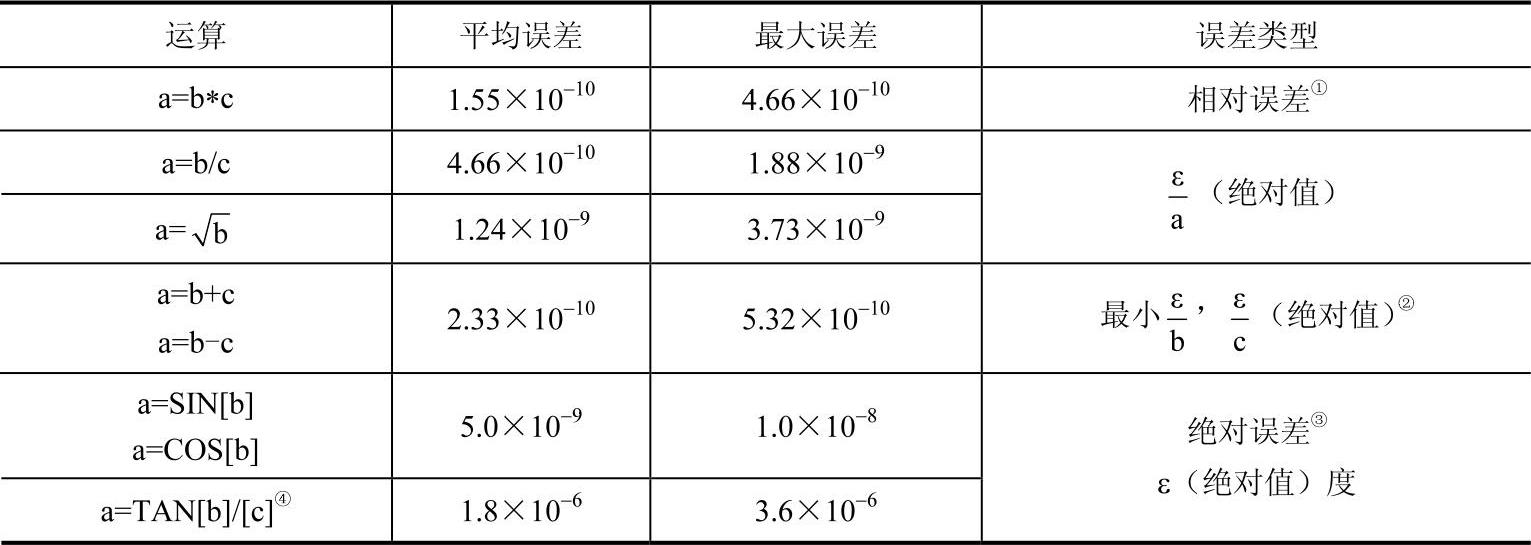
注：如果SIN、COS或TAN函数的运算结果小于10^-8或由于运算精度的限制不为0的话，设定参数No.6004#1为1，则运算结果可视为0。

①相对误差取决于运算结果。

②使用两类误差的最小者。

③绝对误差是常数，而不管运算结果。

④函数TAN执行SIN/COS。

说明：

1）加减运算。由于用户宏程序变量值的精度仅有8位十进制数，当在加减运算中处理非常大的数时，将得不到期望的结果。

例如：当试图把下面的值赋给变量#1和#2时：

#1=9876543210123.456

#2=9876543277777.777

变量值实际上已经变成：

#1=9876543200000.000

#2=9876543300000.000

此时，当编程计算#3=#2-#1时，其结果#3并不是期望值67654.321，而是#3=100000.000，显然误差较大，实际计算结果其实与此还稍有误差，因为系统是以二进制执行的。

2）逻辑运算。逻辑运算即使用条件表达式EQ、NE、GT、GE、LT、LE时，也可能造成误差，其情形与加减运算基本相同。

例如：IF[#1EQ#2]的运算会受到#1和#2误差的影响，并不总是能估算正确，要求两个值完全相同，有时不可能，由此会造成错误的判断，因此应该改用误差来限制比较稳妥，即用IF[ABS[#1-#2]LT 0.001]代替上述语句，以避免两个变量的误差。此时，当两个变量差值的绝对值未超过允许极限（此处为0.001），就认为两个变量的值是相等的。

3）三角函数运算。在三角函数运算中会发生绝对误差，它不在10^-8之内，所以注意使用三角函数后的积累误差。由于三角函数在宏程序的应用非常广泛，特别在极具数学代表性的参数方程表达上，因此必须对此保持应有的重视。