非同轴光学系统优化角度参数模型

水下同步扫描激光周视探测系统，采用折转的光路结构，在扫描过程中激光束发射中心与接收中心分别为发射反射镜和接收反射镜的中心，根据扫描折转机构的设计，发射中心与接收中心不同轴，因此本系统属于非同轴光学系统。对非同轴光学系统而言，其激光束和探测视场的交会关系和分布情况，将对系统探测性能产生严重影响，而探测区的分布情况决定于系统的发射角、接收角、发射光束束散角、接收系统视场角，以及发射中心与接收中心的距离等参数。

现有的激光探测方面的研究主要针对传输介质对光能量的衰减、系统信噪比、成像质量以及测量精度等方面。Di Huige研究了视场角对多次散射激光雷达接收信号的影响，Liu Xueming分析了视场角与水下成像距离的关系，Wang Quandong比较了机载海洋测深系统最大测量深度受激光脉冲峰值功率、接收视场角、接收口径和光谱接收带宽等的影响，尚未有针对非同轴光学系统探测视场的研究。

9.2.3.1　非同轴光学系统探测区分布研究

为最大限度地利用发射激光能量，增大目标回波功率，激光探测系统应尽可能采用同轴结构，使激光发射器和接收器的中心轴线重合，如图9.9所示。但多数激光探测系统，尤其是在激光引信中，由于受到体积、结构、成本等方面的限制，无法采用同轴结构，只能采用发射、接收非同轴结构，如图9.10所示。

图9.9　同轴光学系统

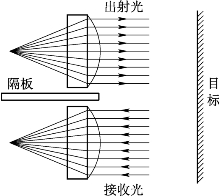
图9.10　非同轴光学系统

设计采用的水下方位识别激光引信光学系统即采用的是非同轴结构，本节针对非同轴光学系统激光束和探测视场的分布情况，以及不同探测区分布对系统探测性能的影响展开研究。

（1）目标回波功率方程

图9.11所示为非同轴光学系统发射光束和接收视场示意情况。

图9.11　发射光束与接收视场示意

点Ot为激光出射中心（即系统中发射反射镜中心），点Or为接收系统中心（即系统中接收反射镜中心），OtOr的连线与轴线重合并规定连线中Or的方向为正方向，发射中心与接收中心的距离为d。系统中，发射角为发射光束中心与轴线方向的夹角αt，发射光束发散角为θt，接收角为接收视场中心与轴线方向的夹角αr，接收视场角为θr，发射反射镜反射率为ηm，接收反射镜反射率均为ηn，发射光学系统透过率为ηt，接收透镜的透过率为ηr，窄带滤光片的透过率为ηa。假设激光发射脉冲的峰值功率为Pt，激光发射方向与目标平面法线之间所夹锐角为θ，目标平面法线与激光视场方向所夹锐角为θs。

以Or点为起点，若目标位于距激光引信R处，R处发射光束截面积S（R）=1/4πR2。由于发射光束的束散角很小，在R=10m处发射光束截面面积S为mm2数量级，远小于潜艇、舰船等目标的截面积，故鱼雷激光引信的所有探测目标均为扩展目标，即发射光束仅照射目标表面的一小块区域。

位于R处的目标被激光束照亮的面积为S（R）/cosθ，计算目标所受的激光照度E（R）：

其中，海水透过率T（R）与海水的衰减系数c满足下式：

则接收视场角内目标的辐射通量Φ（R）：

式中，S1（R）为R处发射光束与接收视场角相交截面面积，S1（R）/cosθ表示R处接收视场角内目标被照亮的光斑面积。假设目标表面的平均反射率为ρ，且目标平面满足朗伯余弦定律，即任意方向上的辐射亮度相等而辐射强度与观测方向相对于辐射表面法线夹角的余弦成正比，则目标在视场角方向的辐射强度：

可得接收系统所探测到的回波功率Pr（R）：

式中，Ω为目标表面被照亮的光斑面积元对接收系统的立体角，若接收系统的有效孔径面积是Ar，则有：

将式（9.58）和式（9.62）代入式（9.61）可得回波功率方程的最终形式：

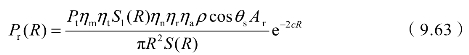
定义η=ηmηtηnηrηa为光学系统总透过率，令k（R）=S1（R）/S（R），定义k（R）为比例系数，表示R处发射光束与接收视场角相交截面面积与发射光束截面面积之比，式（9.63）可简化为：

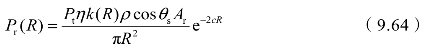
式中，0≤k（R）≤1，与回波功率成正比。若k（R）=0，即S1（R）=0，则表示发射光束不与接收视场角相交，此时Pr（R）=0，接收系统无回波信号，称为探测盲区。若k（R）＞1，即S1（R）＞S（R），则表示发射光束仅有一部分在接收视场角内，此时若其他参数保持不变，则对于同样的距离R，Pr（R）在0与最大值之间变化，称为过渡区。若k（R）=1，即S1（R）=S（R），则表示发射光束全部在接收视场角内，此时若其他参数保持不变，则对于同样的距离R，Pr（R）取得最大值，发射激光的能量被最大限度地利用，称为充满区。

（2）不同角度参数条件下探测区的分布情况

为了充分利用发射激光能量，增大激光回波功率，应尽可能使探测目标处于充满区，但由于发射系统和接收系统不同轴，所以必定存在盲区和过渡区。对不同的系统角度存在不同的探测区分布情况（图9.12），其中M区域为盲区、H区域为过渡区、W区域为充满区。

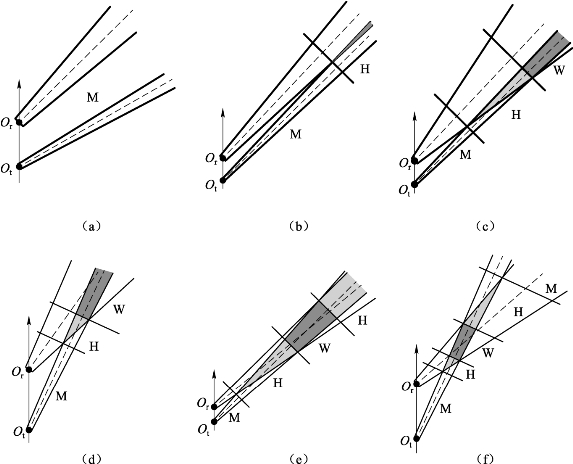
图9.12　探测区分布情况

M—探测盲区；H—探测过渡区；W—探测充满区

根据图9.12（a）～（f）可推知探测区分布情况下的系统角度参数条件，如表9.5所示。

表9.5　不同系统角度分析

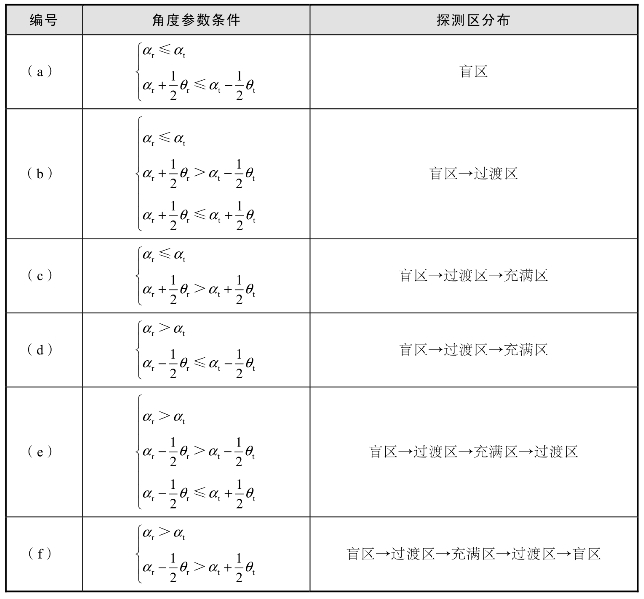
由表9.5可知，图9.12（a）和（b）系统角度参数条件下不存在可利用的充满区，在激光引信角度设计时应避免；图9.12（c）～（f）系统角度参数条件下均出现充满区，其中图9.12（c）和（d）条件下当距离R大于一定值后探测区均为充满区，图9.12（e）和（f）条件下随距离R的增大充满区出现后消失，在实际设计中应根据激光探测系统的具体使用要求选择最合适的角度参数条件。

（3）扫描折转机构角度参数调节

根据前节中扫描折转结构的设计，鱼雷方位识别激光引信采用反射镜折转光束，通过调整反射镜的安装角度来调节系统的发射角αt和接收角αr。当反射镜转动时，对于固定的入射光角度来说，出射光角度变化如图9.13所示。

当反射镜处于初始位置P1时，其法线为N1，入射光线的入射角为I1，根据反射定律入射角等于出射角，此时入射光线与反射光线之间的夹角为2I1。反射镜旋转β角后位于P2位置，法线为N2，此时入射光线的入射角I2等于I1+β，入射光线与反射光线的夹角变为2I1+2β。由此可知，固定入射光线不变，当反射镜转动β角时，反射光线将转过2β角。

图9.14所示为系统中扫描折转机构的角度调节示意图，其中激光器中心和接收器中心均与雷轴重合，规定接收反射镜方向为雷轴的正方向。对于给定发射角αt，应调节发射、反射镜与雷轴夹角βt=αt/2；对于给定接收角αr，则应调节接收反射镜与雷轴夹角βr=（π+αr）/2。

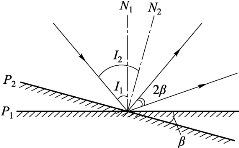
图9.13　反射镜转动示意

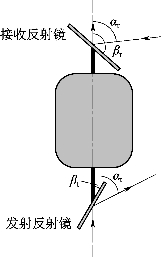
图9.14　扫描折转机构角度调节示意

（4）基于屏蔽干扰信号的角度参数优化

根据上述分析，显然，设计激光探测光学系统角度时应结合性能要求选取图9.12（c）～（f）中的角度参数条件，而规避使用图9.12与表9.5中的（a）和（b）的角度参数。图9.15对发射光束与接收视场交会情况进行了详细描述。

分析图9.15所示非同轴激光探测系统发射光束与探测视场的交会情况可知，发射光束与接收视场相交于A、B、C、D四点，随着与点Ot间的距离逐渐增大，探测区不断变化：在点A之前均为近端探测盲区；由点A开始盲区结束进入过渡区，此时点A与点Ot的距离Rn为近端盲区距离；点B至点C之间为充满区，点B与点Ot的距离Rs称为充满区起始距离，点C与点Ot的距离Rd称为充满区截止距离；点D以后为远端的探测盲区，远端盲区距离Rf即点D与点Ot的距离。

图9.15　发射光束与接收视场交会示意

根据角度关系可知，点B存在即出现充满区的条件是：

点C存在即充满区截止的条件是：

当式（9.66）不成立时，表示充满区将延伸至无穷远处，自点B以后均为探测充满区，即为图9.12（c）和（d）的探测区分布情况。分别计算B点和C点到激光发射中心Ot点的距离。根据正弦定理有：

可得充满区起始距离Rs：

同理，计算充满区截止距离Rd：

近端盲区距离Rn：(www.xing528.com)

远端盲区距离Rf：

根据式（9.68）～式（9.71），Rs、Rn、Rd和Rf均与发射和接收中心间距d成正比，当d=0.18m时，保持αr=90°、αt=88.5°、θr=1.9°、θt=0.1°中的另外3个元素固定不变，分别绘制αt、αr、θt和θr经归一化后对Rs、Rn、Rd和Rf的变化曲线，如图9.16所示。

图9.16　归一化后αt、αr、θt和θr对Rs、Rd、Rn和Rf的变化曲线

（a）sR变化曲线；（b）nR变化曲线；（c）dR变化曲线；（d）fR变化曲线

由图9.16可知，除θt的曲线外，Rs和Rn变化曲线以及Rd和Rf变化曲线基本一致；Rs对αt的变化最为敏感，其次是θt，而αr和θr的变化对Rs的影响非常小；Rn仅对αt的变化敏感，其余三个角度的变化对Rn影响很小；所有角度参数变化均对Rd和Rf有显著影响，其中Rd对θt的变化率较其他曲线稍弱。

根据图9.16可知，Rs、Rn、Rd和Rf均随发射角αt增加而增大，在αt大于某一值后迅速增长；随αr增大而减小，其中Rd和Rf迅速减小并在到达某一值后变平缓。在图9.16（c）和（d）中，αt和αr曲线关于横轴0.35位置处对称，表明增大αt和减小αr对Rd和Rf的增大所起的作用相同。Rs和Rn随θr增加缓慢减小，Rd和Rf随θr增加迅速增加且变化规律相同；Rs随θt单调递增，Rn随θt增加缓慢减小，Rd随θt单调递减，Rf对θt的增加有十分显著的增长。

对于激光探测系统而言，发射光束束散角θt和接收视场角θr可变化范围较小，而发射角αt和接收角αr改变最为容易，根据设定的探测区距离，建立系统接收角αr的计算模型。如已知充满区起始距离Rs、充满区截止距离Rd、近端盲区距离Rn或远端盲区距离Rf以及其他系统参数，可求得接收角αr的充满区临界值αrs、αrd以及近端盲区临界角αrn和远端盲区临界角αrf：

由于Rs、Rn、Rd和Rf均随发射角αt增加而增大，因此可根据所求的αrs、αrn、αrd和αrf分别确定αr解的集合，再通过求多个集合的交集最终确定αr的取值范围。假设某一非同轴激光探测系统要求Rs≥3m、Rd≥11m、d=0.18m，αt=90°、θt/2=0.05°、θr/2=0.95°，计算得αrs=92.58°，αrd=91.89°，故对接收角αr的要求是αr≥92.58°。

9.2.3.2　基于不同探测条件的角度参数优化模型

（1）近程目标探测系统

水下同步扫描激光周视探测系统用于近程探测目标，仅对近程的探测区有要求，而对设计探测距离外的探测区分布无限制。原则上根据近程激光探测系统的探测需求其探测范围是以最大探测距离为半径绕轴心旋转而成的圆形面，但对非同轴光学系统而言盲区不可避免，因此要求盲区越小越好，近程探测适用于图9.12与表9.5中（e）和（f）的角度参数条件。

根据探测要求，近程探测系统应在满足充满区截止距离Rd大于最大探测距离Rmax的条件下，通过角度参数的优化设计，使得充满区起始距离Rs和近端盲区距离Rn最小。同远距离探测系统角度参数优化过程一样，在优化计算时，发射角αt为定值，给定发射光束束散角θt、发射接收中心间距d、接收角αr和接收视场角θr的取值范围，在Rd≥Rmax的条件下求取Rs［式（9.68）］和Rn［式（9.70）］的最小值及对应的系统参数取值。采用多岛遗传算法，在iSIGHT软件中，对近程探测系统的角度参数进行优化。优化中给定的参数如表9.6所示。

表9.6　基于近程探测的角度参数优化中的给定参数

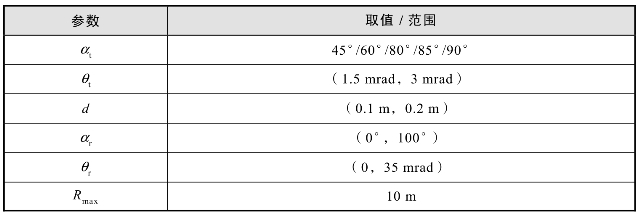
约束条件是：

优化目标为：获得式（9.68）和式（9.70）的最小值。

经过优化后，所得结果列于表9.7。

表9.7　基于近程探测的角度参数优化结果

由表9.7可知，无论发射角αt的取值是多少，在基于近程探测的角度参数优化中，发射接收中心间距d、发射光束束散角θt和充满区截止距离Rd均取其约束范围内的最小值，而接收视场角θr取其约束范围中的最大值时，探测系统具有最小的近端盲区距离Rn和充满区起始距离Rs。设计系统时可直接将发射接收中心间距d和发射光束束散角θt取范围内的最小值，而接收视场角θr取其允许范围的最大值。在限制充满区截止距离Rd最小值的条件下，随着发射角αt的增大，使Rn和Rs取得最小值的接收角αr与发射角αt的差值逐渐增大，但增幅逐渐减小，当发射角αt为85°和90°时，接收角αr与发射角αt的差值相同，均为1.53°。

（2）远距离激光探测系统

远距离激光探测系统，如某些定高引信、激光雷达，探测距离范围大，回波信号微弱，而非同轴光学系统的盲区和过渡区无法避免，为保证探测到目标并充分利用发射功率，要求探测区在一定距离以后均为充满区且尽可能增大充满区范围，即减小充满区起始距离Rs。

根据表9.5可知，方案（c）和（d）均能满足当R大于一定值后探测区均为充满区的条件，但是在图9.12中，发射光束一直处于接收视场的下半部，没有充分利用接收视场，而在图9.12（d）中可以使发射光束处于接收视场的中心位置，因此，方案（d）的探测区分布情况要优于方案（c），对于远距离激光探测系统应选用图9.12（d）中的探测区分布情况，即角度参数条件如表9.5（d）所示：

求解基于远距离探测的光学系统最佳角度参数，即在满足式（9.77）的约束条件下，求取Rs的最小值及取得最小值时的各参量值。

由于改变αt和αr对探测区距离分布影响相同，可任选择其中之一作为定值，本书均以αt作为定值。在设计系统过程中，通常发射角αt按照系统性能需求确定，本书中选取45°、60°、80°、85°和90°分别进行优化。

由式（9.68）可知，充满区起始距离Rs与发射接收中心间距d成正比，当d=0时，即为同轴光学系统，Rs等于0，所有探测区均为充满区。但实际上，非同轴光学系统的发射接收中心间距必然受制于系统结构，不能无限制地减小。在基于远距离探测光学系统的角度参数设计时，约束条件式（9.77）对d并无限制，为减小充满区起始距离Rs，应在结构允许条件下采用最小的发射接收中心间距d，故在优化仿真时d作为定值。

利用iSIGHT优化软件，基于多岛遗传算法，对角度参数进行优化计算，以获得不同αt取值情况下满足条件式（9.77）的最小充满区起始距离Rs及其所对应的系统角度αr和θr。计算时给定的参数如表9.8所示。

表9.8　基于远距离探测的角度参数优化中的给定参数

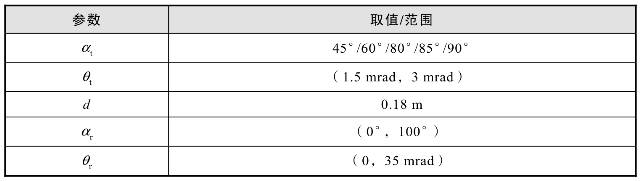
约束条件是：式（9.77）。优化目标为：获得式（9.68）的最小值。

优化结果列于表9.9。

表9.9　基于远距离探测的角度参数优化结果

根据表9.9的优化结果可知，在基于远距离探测的角度参数优化中，发射光束束散角θt越小，接收视场角θr越大，则充满区起始距离Rs越小，设计系统时可直接选取可选择范围内θt的最小值和θr的最大值。对不同的发射角αt，当Rs取最小值时，接收角αr与发射角αt的差值均为0.96°，在基于远距离探测系统中可直接设计接收角αr比发射角αt大0.96°。

（3）基于屏蔽干扰信号的角度参数优化

某些激光引信由于结构限制，需要将激光引信的发射、接收系统后置，使弹体自身的一部分位于激光引信视场中，这可能导致引信“虚警”。为防止引信误触发，可在激光引信光路设计时通过对角度参数的优化，使弹体自身处于探测盲区中，从而屏蔽干扰信号。另外，对于水下激光探测系统，由于海水介质对光信号有强烈的散射作用，近距离处的后向散射光将对系统的信噪比造成很大影响；也可通过调节系统角度，使系统附近为探测盲区，以此减少后向散射光的干扰。这类给定探测范围的情况同样适用于图9.12与表9.5中（e）～（f）的角度参数条件。

若激光引信自身需屏蔽的距离为Rmin，最大探测距离为Rmax，应保证满足近端盲区距离Rn大于屏蔽距离Rmin且充满区截止距离Rd大于最大探测距离Rmax；同时，尽可能增大探测充满区范围，即减小充满区起始距离Rs。在优化过程中，发射角αt设为定值，给定发射光束束散角θt、发射接收中心间距d、接收角αr和接收视场角θr的取值范围，在Rn≥Rmin且Rd≥Rmax的条件下，求取Rs［式（9.68）］的最小值及对应的系统参数取值。选用多岛遗传算法，在iSIGHT软件中，对给定探测范围的光学系统角度参数进行优化。优化中给定的参数如表9.10所示。

表9.10　基于给定探测范围的角度参数优化中的给定参数

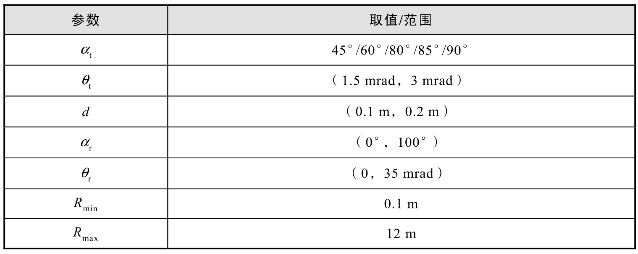
约束条件是：

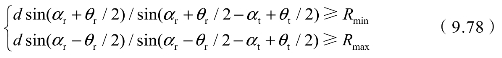
优化目标为：获得式（9.68）的最小值。

经过优化后，所得结果列于表9.11。

表9.11　基于给定探测范围的角度参数优化结果

由优化结果表9.11可知，在基于给定探测范围的角度参数优化中，发射接收中心间距d、发射光束束散角θt和充满区截止距离Rd均取其约束范围内的最小值，而接收视场角θr取其约束范围中的最大值时，探测系统具有最小的充满区起始距离Rs。设计系统时可直接将发射接收中心间距d和发射光束束散角θt取范围内的最小值，而接收视场角θr取其允许范围的最大值。随着发射角αt的增大，使Rs取得最小值的接收角αr与发射角αt的差值逐渐增大，但增幅逐渐减小。

（4）几何截断定距探测系统

对于激光定距探测系统，除了脉冲测距和相位法测距外，也可依据几何截断定距原理，通过结构上角度参数的设计，当几何截断定距探测系统探测到目标时，即表明目标已进入设定距离以内。由于这类激光探测系统作用距离通常较近，所以可以通过适当增强发射功率保证即使目标处于探测过渡区也能够被识别。

在设计此类探测系统时，对已知作用距离，设计近端盲区距离Rn等于R1、远端盲区距离Rf等于R2，同时应最小化充满区起始距离Rs，并最大化充满区截止距离Rd。优化过程与前文一致。在优化计算时，发射角αt为定值，给定发射光束束散角θt、发射接收中心间距d、接收角αr和接收视场角θr的取值范围，在Rn=R1且Rf=R2的条件下求取Rs［式（9.68）］的最小值、Rd［式（9.69）］的最大值，以及对应的系统参数取值。采用多岛遗传算法，在iSIGHT软件中，对几何截断定距系统的角度参数进行优化。优化中给定的参数如表9.12所示。

表9.12　基于几何截断定距的角度参数优化中的给定参数

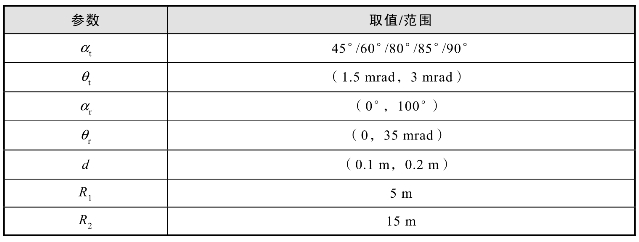
约束条件：

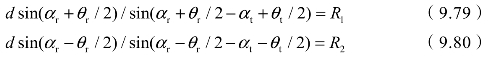
优化目标为：获得式（9.68）的最小值、式（9.69）的最大值。

经过优化后，所得结果如表9.13所示。

表9.13　基于几何截断定距的角度参数优化结果

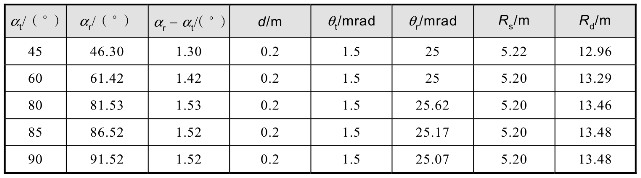
根据表9.13可知，对基于几何截断定距的角度参数优化，应尽可能减小过渡区的面积而增大充满区面积，使充满区起始距离Rs接近近端盲区距离Rn，且充满区截止距离Rd接近远端盲区距离Rf；对不同的发射角αt，优化后的充满区起始距离Rs基本相同，但充满区截止距离Rd随发射角αt增大而略有增大；对各发射角αt取得最佳Rs和Rd的发射接收中心间距d以及发射光束束散角θt均相同。