海水激光传输特性模型分析

9.2.2.1　海水光学特性

海水是一个复杂的化学、物理、生物系统，包含溶解物质、悬浮体，以及多种多样的活性有机体。海水成分的各种不均匀性，使得其间传输的光将被强烈地散射、吸收而衰减。海水中占绝大比例的成分是纯水，水分子是极化的，在紫外和红外谱带上存在强烈的共振，造成纯水对这部分光谱表现出强烈的吸收。但水分子在可见光谱带的共振较弱，纯水在可见光波段的吸收要比紫外和红外小得多，其中，在蓝绿波段450～580 nm吸收最小，吸收系数在0.02～0.05m-1，因此海洋中的光探测都使用蓝绿激光。

大洋中的海水所处的物理条件为：温度-4℃～36℃，压力101 kPa～1.1×108Pa。在该范围内，纯水的光学特性变化很小，海水光学特性的变化主要是由溶解物质和悬浮粒子的不确定性所引起的。海水中对光学特性产生影响的主要有以下几种成分：藻类细胞，如浮游植物，其浓度有很大变化；连带的碎屑，即由浮游生物的自然死亡降解和浮游动物的消化排泄产生的碎屑；悬浮泥沙，即沿岸海底和浅海区因海流等作用而搅起的泥沙；溶解的有机物质；矿物质；细菌等。此外，海水中还包括气泡、一些无机盐（如NaCl，MgCl2、KCl、CaSO、MgSO4等）和气体（如氧气、氮气、二氧化碳、氩气等）。其中，海水中有一部分溶解有机物对水体的光学特性有很大影响，这部分溶解有机物有着特殊的光吸收特性，被称为有色可溶性有机物（Chromophoric Dissolvable Organic Matter，CDOM），由于在黄色波段吸收最小，所以呈黄色，国内多将其简称为黄色物质。

海水中各成分以及环境因素对光的衰减特性总结为表9.1。

表9.1　海水各成分对光的衰减特性

续表

海水的光学特性主体上可分为两个类型进行描述，即固有光学特性（IOP）和表观光学特性（AOP）。固有光学特性仅决定于传输介质本身，独立于介质周围光场，主要参数包括衰减系数、吸收系数、散射系数、体散射函数、折射率、单次散射反照率等。表观光学特性与固有光学特性以及介质周围光场的结构相关，主要参数有辐射照度反照率、漫反射衰减系数、平均余弦值等。

当辐射功率为Φi（λ）（单位W）的单色窄光束垂直照射体积ΔV、厚度Δr很小的水时，水固有的光学特性如图9.4所示。

图9.4　水固有的光学特性定义

根据图9.4可知，入射功率Φi（λ）的Φa（λ）部分被水体吸收，Φs（θ；λ）表示角度θ方向的散射光功率，其中θ称为散射角且0≤θ≤π，其余透射光功率Φt（λ）沿入射方向传播。假设所有散射均为弹性散射，以Φs（λ）表示所有方向的总散射功率，根据能量守恒定律，有：

光谱吸收率A（λ）为吸收功率与入射功率的比值：

光谱散射率B（λ）定义为：

光谱透射率T（λ）定义为：

显然：

在实际测量中，分光光度计无法直接测量吸收率，所测的数据为吸光率D（λ），也称为光学密度，其定义为：

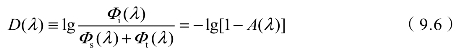
在海洋光学中，光谱吸收和散射系数分别指介质中每单位距离的光谱吸收率和散射率，故光谱吸收系数a（λ）定义为：

光谱散射系数b（λ）定义为：

光束衰减系数c（λ）定义为：

对应于衰减系数c，衰减长度l=1/c表征辐射通量衰减为e-1时所通过的路程。

定义B（θ；λ）表示在散射角θ方向立体角ΔΩ内的总光谱散射率，则θ方向单位距离、单位立体角内的角散射率，也称为体散射函数β（θ；λ）可表示为：

结合辐射强度公式：

以及辐射照度公式：

式中，ΔV=Δr×ΔA。联立式（9.10）、式（9.11）、式（9.12）有：

β（θ；λ）的物理意义是单位入射辐照度在单位体积水散射角方向的散射强度，也表示单位体积的微分散射截面。对β（θ；λ）在所有方向（立体角）进行积分，就可以得到单位辐照度入射到单位体积水的散射功率，即光谱散射系数：

在式（9.14）中，由于自然水体中散射在入射方向是关于散射角对称（非极化光源和随机定向散射），按照散射方向与入射方向的夹角将散射分为前向散射（0≤θ≤π/2）和后向散射（π/2≤θ≤π）两部分。前向散射系数和后向散射系数分别为：

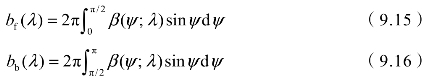
定义光谱体散射相函数P（θ；λ）为：

体散射相函数表示光在某个给定方向单位立体角中散射的能量与在所有方向上平均的单位立体角中的散射能量之比，反映了散射体在0°～360°各散射角方向上对光的散射能力，是描述散射特性的重要参数。

联合式（9.14）和式（9.17）可得相函数的归一化条件：

当涉及水体中光场分布时，固有光学特性不再适用，而需要通过表观光学特性的相关参量来加以描述。不同固有光学特性，表观光学特性不能通过选取水体样本进行测量，它依赖于水体周围的辐亮度分布。表观光学特性中最主要的参量为平均余弦g，其定义为散射角θ的余弦在所有散射方向的平均值：

平均余弦g通常叫作相函数的不对称参数，表征相函数的“形状”。例如，如果θ很小，P（θ）非常大，那么g接近1；如果P（θ）关于θ=90°对称，则g=0。

9.2.2.2　激光束在海水中的能量衰减模型

在研究水下激光束的传输过程时，海水介质中的各种成分对光束的作用都可以归结为对光波的吸收和散射。海水对近红外光的吸收与温度有很大关系，但在可见光波段，温度和盐度对吸收系数的影响非常小，基本可以忽略。对于532 nm绿激光海水的光学特性主要与4种因素有关：纯水、黄色物质、浮游植物和非色素悬浮粒子。其中，黄色物质对光仅有吸收作用，其他3种成分对光既有吸收作用又有散射作用。因此，海水的吸收系数是纯水、黄色物质、浮游植物以及非色素悬浮粒子的吸收系数之和：

式中，下标w，y，ph，d分别代表水分子、黄色物质、浮游植物和非色素悬浮粒子对光的吸收作用。而海水的散射系数是浮游植物、非色素悬浮粒子以及纯水的散射系数之和：

联立式（9.9）、式（9.20）和式（9.21）可得海水的总衰减系数c（λ）的计算公式：

水下激光探测系统采用532 nm绿激光，针对532 nm波长的光波计算海水的吸收系数a（532）、散射系数b（532）和衰减系数c（532）。

（1）海水吸收系数

海水光吸收表现为入射到海水中的部分光子能量转化为其他形式的能量，如热动能、化学势能等，所以海水的光吸收表现出的是衰减机制。

很多学者采用多种方法对纯水吸收光谱进行了大量的测量工作。然而不同的人所得到的测量结果有明显的差异。这表明纯水吸收光谱的测量有很大程度的不确定性。这些不确定性主要来自水中杂质散射的影响。中山大学的邓孺孺等人设计了一套采用较直接方式测量水体吸收系数的新装置，最终得到较准确的纯水在400～900 nm波段的吸收系数。其中，纯水对532 nm波段的吸收系数为0.042 4m-1，即：aw（532）=0.042 4m-1。

黄色物质是指海洋中的有色可溶性有机物（CDOM），该物质具有特殊的光吸收性，从光谱曲线可见，其与纯海水形成鲜明对比。黄色物质的吸收光谱关系可用式（9.23）表示：

式中，ay（λ）和ay（λ0）分别表示在波长λ和λ0处的吸收系数，m-1；S为光吸收谱的斜率。朱建华和李铜基利用春季黄海海区现场测量的黄色物质光谱吸收系数数据，分析评价不同参考波长拟合吸收系数曲线斜率的差别和效果。结果表明，λ0=440 nm时，拟合效果最好。此时，a（λ0）=0.078 3m-1，S=0.017 5，即，

可计算得532 nm波段黄色物质的吸收系数：ay（532）=0.015 6m-1。

浮游藻类光谱吸收曲线由进行光合作用的活性叶绿素a和其他辅助色素浓度决定，而它们的浓度随着水体环境和藻类的不同而变化，其中起主导作用的是叶绿素a对光的吸收作用。

浮游植物对光的吸收可以用式（9.25）来进行计算：

式中，（λ）为叶绿素a的单位吸收系数，即单位浓度叶绿素（1mg/m3）的吸收系数，[Chl]为叶绿素a的浓度（mg/m3）。对于单位吸收系数（λ）有公式：

其中，A（λ）为在参考波长λ=440 nm处进行归一化以后的单位吸收系数，即有：A（λ）=aph（λ）/aph（440）。B（λ）反映单位吸收系数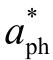（λ）随叶绿素浓度增加而减小的速率。联立式（9.25）和式（9.26）可得：

引用Howard R.Gordon的研究结果，对式（9.27）参数化：

对于532 nm波段，A（532）=0.34，代入式（9.28）得：

aph(532)=0.020 4 [Chl]0.602

非色素悬浮物是由浮游植物死亡而产生的有机碎屑以及泥沙等颗粒经再悬浮而产生的无机悬浮颗粒。非色素悬浮粒子的吸收系数与波长也呈指数关系，和黄色物质具有非常相似的吸收光谱，表示为：

式中，ad（λ0）为参考波长下非色素悬浮粒子的光吸收系数，一般取λ0=440 nm。Sd为光吸收谱斜率，平均值为0.01±0.002。在这里取ad（440）=0.198m-1，Sd取平均值0.01，即：

(www.xing528.com)

当λ=532 nm时，ad（532）=0.078 9m-1。

（2）海水散射系数

光和粒子的相互作用，按粒子尺度r与入射波波长λ的相对大小的不同，可采用不同的处理方法。通常将粒子考虑为均匀球状体，常采用无量纲尺度参量α=πr/λ作为判别标准：当α≪1时，属于瑞利散射；当α≈1时，属于米氏散射；当α≫1时，属于漫反射，可用几何光学处理。由于水分子粒子尺寸远远小于探测光波长，所以海水中水分子的散射可以用瑞利散射理论来进行处理。由此Raymond C.Smith和Karen S.Baker在1981年给出纯水水分子的散射系数计算公式：

考虑到海水中所含盐分，本书采用文献所得的35‰～39‰的纯盐水的散射系数：bw（532）=0.002 2m-1。

由于浮游植物和非色素悬浮粒子的尺度与光波波长相当，故其所引起的散射一般用米氏散射理论处理。MOREL给出浮游植物的散射系数与波长的经验关系，为：

式中，bph（550）为550 nm处的散射系数，可表示为bph（550）=Bc[Chl]0.62，其中Bc为常量，取值0.12，单位为mg/m3，则有：

当λ=532 nm时，bph（532）=0.124[Chl]0.62。

与浮游植物散射系数的计算方法相类似，对于非色素悬浮粒子的散射系数有：

其中，bd（550）是参考波长取550 nm时非色素悬浮粒子的散射系数，有bd（550）=0.125D′，D′是海水中非色素悬浮粒子的质量浓度，单位为mg/L。故：

当λ=532 nm时，bd（532）=0.129D′。

综上可得532 nm波段的光波在海水中的总衰减系数：

（3）海水中目标回波功率衰减模型

目标回波功率方程：

式中，Pr（R）表示探测器所接收到距离R处的目标的回波功率；Pt为激光器发射功率；η为光学系统总透过率；c为海水的衰减系数；ρ为目标表面的平均反射率；Ar为接收系统的有效孔径面积；θs为目标平面法线与激光视场方向所夹锐角。

将532 nm波段的光波在海水中的总衰减系数式（9.36）代入式（9.37），可得532 nm激光探测系统在海水中的回波功率衰减模型：

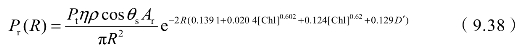
根据式（9.38），目标回波功率与叶绿素a的浓度[Chl]（mg/m3）、海水中非色素悬浮粒子的质量浓度D′（mg/L）密切相关，给定参数如表9.2所示，回波功率相对叶绿素浓度和非色素悬浮粒子浓度变化规律如图9.5所示。

表9.2　回波功率衰减计算参数

图9.5　回波功率变化规律

（a）随非色素悬浮粒子浓度变化；（b）随叶绿素浓度变化

由图9.5可见，回波功率随粒子浓度的增加呈指数下降，并且对叶绿素浓度的变化更为敏感，当粒子浓度高于一定程度后，探测器将无法接收到目标回波。

（4）水下激光探测系统发射功率要求

对于确定的水下激光探测系统，其接收系统的探测灵敏度是一定的，即接收系统能探测到的最小回波功率Pr一定。变形后可得对应于水下激光近程探测系统探测最远距离Rmax所需的发射脉冲激光的峰值功率Pt（Rmax）：

根据式（9.39）所建立的发射功率模型，在不同的叶绿素a的浓度[Chl]（mg/m3）和非色素悬浮粒子的质量浓度D′（mg/L）条件下，对发射脉冲激光的峰值功率Pt（Rmax）进行仿真。在仿真过程中取：总光学系统透过率η均为0.86，目标表面的平均反射率ρ为0.3，孔径面积Ar=9×10-4πm2，接收系统的探测灵敏度Pr=5μW。一般情况下，海水参数取[Chl]=1mg/m3，D′=0.1mg/L。

针对上述仿真参数，随给定的最远探测距离Rmax由1m到10m增加所需的发射脉冲激光峰值功率Pt（Rmax）增长情况如图9.6所示。

图9.6　发射激光峰值功率Pt（Rmax）变化曲线

分别针对浮游植物粒子占主导和非色素悬浮粒子占主导的水体，即在不同[Chl]（mg/m3）和D′（mg/L）的取值条件下，仿真计算对应于1～10m最大探测距离Rmax（m）所需的发射激光峰值功率值Pt（Rmax），计算结果列于表9.3，其中[Chl]和D′的单位分别为mg/m3和mg/L。

表9.3　不同水质条件下所需发射激光峰值功率值Pt（Rmax）

由仿真结果可知，在给定海水环境下，探测Rmax距离所需要的激光发射功率Pt（Rmax）随Rmax的增加呈指数增长。叶绿素a的浓度[Chl]和非色素悬浮粒子的浓度D′对Pt（Rmax）有显著影响，而且叶绿素a的浓度的影响比非色素悬浮粒子的浓度大。在[Chl]=0.1mg/m3、D′=0.1mg/L的清洁海域，90 W以上的发射脉冲激光峰值功率即可探测到10m处的目标；而在类似于[Chl]=1mg/m3、D′=1mg/L非色素悬浮粒子占主导的清洁二类水体，需要8 kW的发射脉冲激光峰值功率探测10m处的目标；但在[Chl]=10mg/m3、D′=1mg/L浮游植物丰富、非色素悬浮粒子浓度密集的海域，光束能量衰减十分严重，需要超过72 MW以上的发射脉冲激光峰值功率才能探测到10m处的目标。

需要说明的是，在本节中讨论水下探测系统最大探测距离是在仅考虑目标回波强度可被探测器识别的条件下进行的，并未考虑后向散射光以及其他环境光等造成的噪声干扰。在实际中，当后向散射光等噪声强度高于目标回波强度时，即使目标回波强度高于系统探测灵敏度，探测系统也可能无法识别目标。

9.2.2.3　海水后向散射特性

由于水的光学特性较为稳定，而黄色物质对光束仅存在吸收作用，海水中对激光传输影响最大的组分为水中的各类悬浮粒子，包括藻类粒子和非色素悬浮粒子等。这些粒子以不同的质量浓度存在于海水中，对光束产生严重散射作用，除了造成能量衰减以外，与入射方向相反方向的散射光会进入探测器中，与目标回波信号混杂，降低系统的探测信噪比。

光子与水中随机分布的散射体发生作用，光散射方向与原来的入射方向夹角大于90°的部分，即为后向散射。后向散射光主要存在于浅水域，因为这部分海水的悬浮颗粒最多。由于它具有很大的动态范围，并且光强度往往远大于目标反射信号，所以后向散射光是水下激光探测系统中重点研究的部分。

（1）海水悬浮粒子米氏散射模型

海水中悬浮粒子的尺寸参数α接近于1，对于这类粒子的散射通常用米氏散射（Mie）理论加以描述。Mie的强度比瑞利散射大得多，但散射强度随波长的变化不如瑞利散射剧烈，散射光强会随角度变化出现许多极大值和极小值。

根据Mie理论，被一个粒子散射到θ方向的散射光可以分为两个互相垂直的偏振分量，这两个分量分别和两个强度分布函数i1和i2成正比。这两个函数是Mie理论的精髓，可表示为：

式中，S1、S2为散射光的振幅函数，分别为S1、S2的共轭复数，α为粒子尺寸参数（α=2πR/λ），m=n-ini为粒子相对周围介质的折射率，当虚部不为零时，表示粒子有吸收。S1、S2可表示为下列无穷级数：

式中，an和bn的值由Ricatti-Bessel函数决定，由下式计算得到：

式中，

（cosθ）为一阶n次第一类缔合勒让德函数，Jn+1/2（α）是半整阶贝塞尔函数，J-n+1/2（α）是负半整阶贝塞尔函数。

粒子的衰减系数c与粒子尺寸参数α以及粒子复折射率m密切相关。根据Mie理论计算公式绘制同一粒子不同复折射率虚部ni条件下，衰减系数c随尺寸参数与折射率实部乘积ρ=2α（n-1）变化的曲线，如图9.7所示。

由图9.7可知，衰减系数c随着参数ρ增大呈现以2为振荡中心、振幅依次减小的一系列有规则的振荡变化，当ρ在4附近时，c取得第一次最大值，此后，随ρ增大，振荡振幅依次减小，最终逼近2。因此，当参数4ρ≤时，颗粒的衰减系数在给定波长处，随着颗粒直径的增大而增大；在给定粒径处，随波长的增大而减小。改变复折射率虚部并不会改变振荡峰的位置，只影响振荡幅值，且随着颗粒吸收的增强，振荡幅值降低，且更迅速地趋向稳定值2。

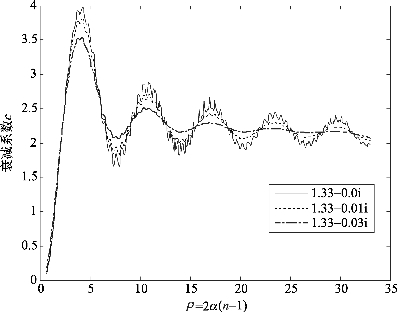
图9.7　衰减系数c随参数ρ变化的曲线

对不同尺寸参数和复折射率的粒子，计算其衰减系数c和散射系数b，计算结果如表9.4所示。

表9.4　部分粒子衰减系数c与散射系数b的计算结果

由表9.4可知，对同一尺寸参数，随着复折射率中虚部的增大，即在传输过程中吸收作用的增强，散射系数与衰减系数的差值增大，当虚部为0时，散射系数等于衰减系数；对同一复折射率，在一定范围内，随粒子尺寸参数的增大，衰减系数将显著增大。

（2）悬浮粒子后向散射率

计算海洋悬浮粒子的后向散射时，应首先获得其散射相函数。根据等效米氏散射理论，散射相函数P（θ）可表示为散射角θ方向的角散射截面a（θ）与所有方向角散射截面平均值σs/4π之比：

式中，

无偏振自然光的散射截面σs为：

联立可得散射相函数P（θ）的计算公式：

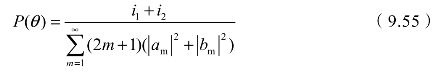
若粒子对532 nm激光的复折射率为m=1.33-0.001i，选取尺度参数α=0.1、10、100、2 000，分别绘制出散射相函数P（θ）的变化曲线，如图9.8所示。

图9.8　不同尺度参数下散射相函数P（θ）曲线

（a）α=0.1；（b）α=10；（c）α=100；（d）α=2000

由图9.8可知，当尺度参数α很小时，散射相函数P（θ）随散射角θ的变化较小，图像围绕θ=π/2几乎呈轴对称分布，散射相函数P（θ）的最小值位于θ=π/2处，前向散射和后向散射近似相等。随着α值的变大，前向散射逐渐变大，后向散射逐渐变小，对称性被破坏，P（θ）的最小值也移至θ=0.17附近。当α进一步增大时，散射图像变得复杂起来。当α =10～100时，从图9.8中可以看出，散射光强主要集中到前向一较小角度范围内，散射相函数P（θ）的分布随散射角θ的变化呈现振荡的现象，出现一些极大值和极小值，后向散射变得比较微弱。当α=2 000时，散射图像变得异常复杂。但是通过观察发现，散射光强主要集中在前向和后向一较小角度范围内，其余范围内虽有散射光强分布，但能量非常小。

通过Mie理论及其散射相函数公式就可以计算出海洋中悬浮粒子的后向散射率，海洋中悬浮粒子的后向散射率γb等于其散射相函数P（θ）在散射角90°～270°的积分值比上其散射相函数在散射角0°～360°的总的积分值。由于散射相函数的分布关于入射光光轴对称，海洋中悬浮粒子的后向散射率的计算可简化到对散射相函数在90°～180°的积分比上散射相函数在散射角0°～180°的积分值：

在蓝绿光波段，γb的典型值在0.000 2～0.015。后向散射率表示在所有散射光中后向散射光所占的比例，其值越大，其对水下探测系统探测目标就越不利。