目标定位算法优化方案

智能雷弹构成的无线网络中包含1个网关节点和数量较多的传感器节点，可通过飞机或火箭大规模部署在远距离监测区域。在每个传感器节点，1个麦克风作为感知设备，1个微处理器用于数据和信号处理，1个无线数据传输模块用于信息交换和1个电池作为电源供应。一定数量的传感器节点每个同时配备1个定位模块获取自身位置，各节点通过射频组成无线多跳自组织网络。本节研究智能雷弹对处于抛撒区域外部声源目标和内部声源目标的定位和跟踪算法，在对误差源分析的基础上提出相应的节点选择算法。由于目标声源运动速度较慢（＞40 km/h），多普勒效应对基于能量的定位算法影响不大，因此在定位算法的分析中并没有考虑多普勒效应。

8.4.2.1　智能雷弹抛撒区域外围目标定位算法

处于智能雷弹抛撒区域外围的目标距离传感器节点较远，因此能够感知到目标的传感器节点也较少。另外，对外围目标的定位任务目的是预警，无须浪费能源有限的WASN大量的资源。因此，与抛撒区域内部目标定位的要求也有所不同。本节依据声压衰减模型和几何定位机制，提出基于能量的四节点声阵列目标定位算法，对处于智能雷弹抛撒范围外的目标声源进行初步定位和预警；在对影响定位算法精度的误差源分析的基础上，进一步提出节点选择算法。

当目标声源接近节点抛撒区域时，网络自组织选择4个最合适的传感器节点，组成声传感器阵列，对目标进行定位。在实际应用中，测量某一时刻的瞬时声压意义不大，往往在一个时间间隔内多次取值，并通过短时能量法求得这段时间内的能量值。根据声音衰减公式并结合几何定位法，提出基于能量法的四元分布式声阵列目标定位算法。但是声音能量衰减公式对于未知量——目标坐标来说是非线性的，会增大后续求解过程的复杂度。因此，通过任意两个不同节点的声音能量衰减模型相减，去除非线性方程中的平方项，并将声源能量看成未知量，从而将非线性方程变为线性方程求解。对于节点i，可得：

令S2/α=Sa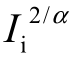，=Ei，上式可转化为：

则节点j得到如下对应的方程：

式（8.40）与式（8.41）相减可得：

此算法最少需要3个独立的方程来求解未知数，因此至少需要4个节点参与目标的定位计算。对于4节点模型，可得如下方程组：

式中，（x，y）表示目标位置；（xk，yk）表示第k个传感器节点的位置。上式可写成矩阵形式：Aq=B。

其中，。由于存在背景噪声，实际测得的声音能量并不准确，导致方程组在求解时产生定位误差

（1）四元无线声阵列目标定位算法误差源分析

定位误差的主要来源是背景噪声，它会导致定位算法产生误差，而不恰当的声音衰减系数和不合理的四节点模型会导致定位误差变大，甚至使定位算法无解。因此，在存在背景噪声的情况下，研究能够使定位误差在合理的范围内的最佳声音衰减系数和四节点模型显得尤为重要。由于节点是随机撒布的，因此很难从数学表达式上分析出形状、尺寸和方位角对误差的影响。本书采用控制变量法来研究，通过大量的仿真计算获取可使误差相对较小的声音衰减系数和最优四节点模型。

1）声音衰减系数。

在实际的测量环境中，声音衰减系数α≠2，若式（8.20）仍然按照α=2进行求解，则会产生较大定位误差。为了量化声音衰减系数对定位精度的影响大小，本节对不同声音衰减系数下的定位误差进行仿真分析。设β=α/2，其中α为实际声音衰减系数，理论声音衰减系数为2，在不同的实际声音衰减的环境中，方程组（8.43）利用实际声音衰减系数与利用理论声音衰减系数的定位误差仿真结果如图8.16所示。

图8.16　噪声衰减系数对定位精度的影响

由图8.16可知，当β＜1时，方程组（8.43）利用理论噪声衰减系数α=2求解的误差值比按实际环境下的α值所得的定位误差值大；而当β＞1时，α=2的定位误差曲线却比实际噪声衰减系数曲线小。因此在对目标进行定位之前，应对测试环境的噪声衰减系数进行测量。若α＜2，则按实际噪声衰减系数进行求解。然而，当α≥2时，噪声衰减系数应当取值为2。

2）无线传声器阵列模型。

4个节点可组成的图形有：线形、圆形和四边形（三角形可被看成四边形的一种特例）。由计算可知，当阵列形状为线形以及圆形时，方程组（8.43）无解。任意不在同一条直线上的四节点模型可被视为圆上3点和圆内或圆外的1点。因此将无线4节点声阵列模型的3点固定于圆上，通过改变另外一点的位置来研究阵列形状对定位精度的影响。无线4节点声阵列模型如图8.17所示。

①　R、a对定位精度的影响。由于模型参数较多，根据控制变量法，将圆内三角形设为等边三角形，节点2的坐标是（Rcos0°，Rsin0°），节点3的坐标是（Rcos120°，Rsin120°），节点4的坐标是（Rcos240°，Rsin240°）。目标的方位设为（Rcos240°，Rsin240°），声音衰减系数α=2。通过仿真可知，当a≤R时，定位误差较大。在a=R时，甚至出现无解的情况。因此在仿真过程中，将a的值设为4～10m，所以当R的值为2m和3m时，节点1在不同角度下的仿真结果如图8.18所示。

图8.17　无线4节点声阵列模型

图8.18　节点1在不同位置时定位误差仿真结果

（a）R=2m；（b）R=3m

图8.18中的极径表示误差值，极角表示节点1的变换角度。由图8.18可知，a的值越大，误差值越小；对比图8.18中（a）和（b）可知，R的值越小，误差值越小。但是根据实际无线传感器网络的部署情况和节点密度的不同，R与a的取值也受到限制，本书取R=2m，a=10m。

②　目标声源与阵列的相对位置。由上节仿真结果可知，目标方位的变化对无线声阵列的定位效果有很大的影响。为了避免阵列与目标声源处在定位误差较大的相对位置上，需研究目标声源与阵列的相对位置对定位精度的影响。在仿真过程中，取R=2m，a=10m，目标距离圆心50m，目标方位角为θ。当节点2、3和4分别组成等边三角形、直角三角形和钝角三角形，目标方位角θ取0，π/4，π/2和3π/4时，节点1在不同角度定位误差的仿真结果如图8.19所示。

图8.19　圆上三点处于不同形状时定位误差仿真结果

（a）等边三角形；（b）直角三角形（c）钝角三角形

对比图8.19中（a）、（b）、（c）可以看出，圆内三角形形状随着目标声源位置的不同所产生的误差趋势是一致的，说明三角形的形状对定位误差影响不大。随着目标声源的方位变化，定位误差随节点1位置变化的曲线相差较大。没有一种阵列模型能够使全向的目标定位精度达到最佳。但是当节点1的方向与目标声源方向夹角为60°～100°时，定位误差达到最小值。基于上述分析，为了方便试验进行，并根据实际研究的项目，本书提出Y型无线声阵列模型，如图8.20所示。

当目标声源在50m的距离上360°变换时，仿真出该模型的定位误差，如图8.21所示。从中可以看出，当目标声源的方位角在60°～100°和260°～300°时，定位误差1mdΔ＜。在实际的节点选择过程中，没有必要一定选取Y型无线声阵列，只需要满足半径R尽可能小、距离a尽可能的大，并且节点1的方向与目标声源方向夹角60°～100°。

图8.20　Y型无线声阵列模型

图8.21　Y型无线声阵列模型目标定位误差

3）阵元高低误差分析。(www.xing528.com)

智能雷弹随机抛撒的区域由于地面不平整，导致智能雷弹节点不是处于同一平面上。目前基于GPS或传感器节点自定位算法都不能分辨出2m的高度误差，因此目标定位算法是否能够容忍高度误差也是判断算法实用性的一种标准。

阵元高低误差如图8.22所示，以节点2所在的平面为基准，节点1、3、4与基准平面的高度差分别为h1，h3和h4。在仿真过程中，hi=Position_error×2×（rand-0.5），i=1，3，4，其中Position_error在0～1m变化，rand是0～1的随机数。阵元高低误差对Y型四元无线阵列的定位精度影响如图8.23所示。图8.23中的每个数据是仿真1 000次后的定位误差平均值。

图8.22　阵元高低误差示意

图8.23　阵元高低误差对Y型四元无线阵列定位精度的影响

由于在仿真过程中引入随机量rand，因此图8.23定位误差随高度误差的变化趋势并非准确，这只能说明当高度误差处于某一范围时无线声阵列的定位误差范围。由图8.23可以看出，当高度误差Position_error＜1m时，Y型四元无线声阵列的定位误差＞0.4m，说明阵元的高度误差对Y型四元无线阵列定位精度影响不大。

（2）节点选择算法

无线传感器网络自组织目标定位算法的核心是在大量节点中选择合适的节点，从而使所提出的四节点无线声阵列的定位算法达到最佳定位精度。本书中无线传感器网络的各节点位置已知，并且采用集中式处理模式，即所有数据处理都可在网关节点上进行。因此在网关节点上可把智能雷弹看成分布在以网关节点为中心、x轴指向东、y轴指向北的直角坐标系中。当某一节点接收到的信号强度达到阈值时，唤醒周边其他节点，并在网关节点上运行节点选择算法。根据上节仿真分析结果，节点选择可通过三个步骤实现，如图8.24所示。

1）通过贪婪搜索算法确定接收能量最大的传感器节点，并以该节点与网关节点的连线作为目标的初始估计方向，如图8.24中的点画线所示。

2）在以Q点为圆心（Q为初始估计方向上距离边界10m远的点）、2m为半径的圆上随意选择3个节点，作为四元无线声阵列的从节点。

图8.24　节点选择算法示意

3）以Q为起点，在80°方向选择距离Q点10m远的主节点。图8.24中上、下两个80°方向可随意选择一个。

由于目标声源相对于阵列轴线的方位角在60°～100°和260°～300°时，阵列定位误差最小，而且初步估计的目标方向误差较大，因此选择80°的偏转角度来确定主节点，以便留有余量容忍初步估计的目标方向误差。在节点选择过程中，可优先按照实际项目确定初始选择方案，如果没有合适的四节点阵列，那么可以修改阵型参数，以得到更优或次优的定位结果，从而增加四元无线声阵列的适应性。当无线声阵列确定后，主节点负责收集其他三个节点的信息，计算出目标的方位。无线传感器网络区域外目标自组织定位过程如图8.25所示。

图8.25　智能雷弹区域外自组织定位流程

由于目标必须在与阵列轴线较为垂直的位置上，所以单个无线四元声阵列的适应性极低。但是有别于传统的固定声阵列，在智能雷弹中可通过选择不同的节点，得到不同形状、位置、大小的无线声阵列，不同的目标可根据角度的约束条件选择与之对应的声阵列。可以简单地认为，智能雷弹中存在无线声阵列的集合，每个不同时刻、不同位置的目标都能在集合中找到合适的无线声阵列。因此对于单个无线声阵列是缺乏普遍性的，但是智能雷弹具有的声阵列集合弥补了这一缺陷。智能雷弹可根据目标的位置不断地更新声阵列，从而实现对运动目标的跟踪。

8.4.2.2　抛撒区域内部目标定位与跟踪算法

由于声源目标处于抛撒区域内部，有可能被更多的传感器节点探测到，因此应充分利用传感器节点的测量信息更加准确地估计目标位置。不同于上节所述的四元无线声阵列，我们将其称为网络目标定位与跟踪。

智能雷弹无线传感器网络中包含m个传感器节点和1个网关节点，网关节点能量充足，计算能力强，满足收集感知信息并最终进行目标声源位置估计的要求。目标声源坐标为（x，y），每个传感器节点的坐标为（xi，yi），其中i代表第i个传感器节点。假设无线传感器网络中有n个节点可感知到目标声源，所得数据可表示为I=[I1，I2，I3，…，In]T，其中Ii表示第i个节点的接收能量值。节点i与目标声源之间的距离di可表示为：

带入声音能量衰减公式Ii（t）=+εi（t），εi为均值为0、方差为σ2的高斯白噪声。令gi=1，可得节点i的定位方程：

由式（8.45）可以看出，定位方程是非线性的，为了减少计算量，需要将非线性的定位方程线性化。上节是通过任意两个不同节点的声音能量衰减模型相减，从而将非线性方程变为线性方程求解。本节通过两个节点的定位方程相除，去除未知量S（t），并引入另外一个变量将非线性方程线性化。

令R=x2+y2，Ei=，Ej=，则式（8.45）可写成：

写成矩阵形式为：

其中，b是（n-1）×1的矩阵，，A是（n-1）×3的矩阵：

矩阵θ是待估计的参数矢量，矩阵A和矩阵b都是观测矢量。式（8.48）为线性超定方程组（亦称为矛盾方程组），此方程组一般无解，但可将问题转化为求使得误差最小时的近似解，也就是寻找出未知数x，y，R的一组数值，使超定方程组中的各式近似相等。根据线性最小二乘法求解超定方程组的原理，可得法方程组为：ATAθ=ATb。因此参数θ的无偏估计值可表示为：

然而，由于各节点距离目标声源距离不同，接收到的信号可信赖程度也不相同，因此加入最小平方权重系数，从而增加目标声源的定位精度。式（8.49）可改写为：

其中，W为最小平方权重系数矩阵，维度为（n-1）×（n-1）。根据观测误差矢量，W-1可表示为：

W的求解需要已知传感器节点坐标和声源目标的坐标，因此在初次估计时，可令W为单位矩阵，待得到目标声源坐标的初始估计值后，再进行第二轮求解。估计误差Δθ的方差为：

利用加权线性最小二乘法（WLLS）求得声源目标坐标的近似估计值，称为非约束加权线性最小二乘法（UWLLS）。但是x，y，R这三个未知数并不是相互独立的，它们之间存在相互约束关系，可通过未知量之间的相互约束关系计算更为精确的坐标位置，我们称之为约束加权线性最小二乘法（CWLLS）。

同样的，内部目标定位也存在定位误差。定位误差的主要来源是背景噪声，会导致定位算法产生误差。另外，节点部署情况、目标声源所处的位置、传感器节点的位置误差、传感器节点的感知范围、声音衰减系数等都会对定位精度产生影响。