探测和处理系统的设计与试验深入探讨

为验证探测和处理系统引信基准误差校正算法的效果，进行了以下试验：第一，引信基准误差测量试验，测量未经校正的引信基准频率，计算其误差；第二，利用前述时钟同步方法校正基准频率，计算校正后的基准误差。

引信基准频率误差校正试验结果如图5.37所示。其中，图5.37（a）为校正前引信基准频率误差，图5.37（b）为校正后引信基准频率误差。试验结果表明，在校正前，引信基准频率散布很大，且散布规律随温度变化而变化。在校正后，基准频率散布变小，且其散布与校正时的环境温度无关，校正前频率分布范围为1.498～1.508MHz，校正后频率分布范围为1.499～1.501MHz。

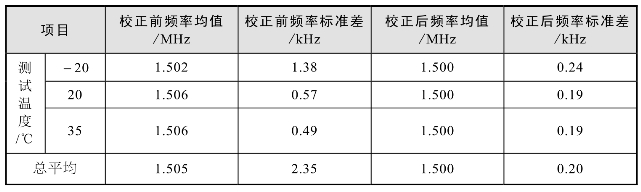
统计表明，校正前，-20℃条件下的基准频率均值与20℃及35℃不同，且散布很大，系统在测试中的总频率散布达到了2.35 kHz。校正后，基准频率均值均为1.500MHz，且标准差在所有温度条件下均小于校正前，其统计结果见表5.5。

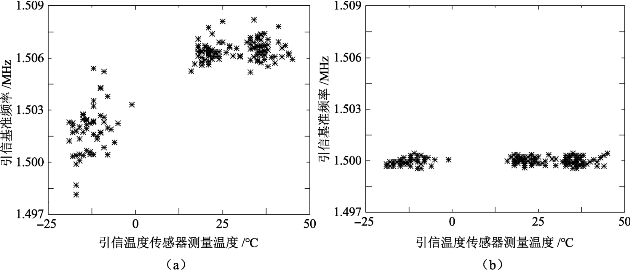
图5.37　引信基准频率误差校正试验结果

（a）校正前引信基准频率误差；（b）校正后引信基准频率误差

表5.5　引信基准频率误差校正试验结果统计

通过不同温度下的1s定时试验验证基准误差校正效果。试验采用50个与图5.37（a）相同批次的引信。对于每个时钟采用的试验方法为：第一，在设定温度下运用装定信息同步法校准初始时钟漂移，记录初始时钟漂移校准结果和1s定时结果；第二，改变温度，根据初始时钟漂移校准结果校准当前时钟漂移结果，记录1s定时结果；第三，重复前两个步骤至试验完成。分别用图5.37（a）的统计拟合结果和前文所述两阶段时钟同步方法校准时钟漂移，记录1s定时结果，对比两种方法的校正结果。

分别在装定信息同步温度为-20℃、0℃和20℃的条件下进行试验，试验中设置温度改变量分别为±5℃和±10℃。50个时钟的试验结果如图5.38所示。对比图5.38（a）、图5.38（b）和图5.38（c）可以看出，不论采用何种同步方法，其精度都随同步温度升高而升高，与前文中的仿真结果一致。从图5.38中可以看出，温度测量修正法的极差与统计拟合修正法相似，但统计拟合法结果分布较为均匀，而采用预测修正法时，大部分时钟的定时结果集中分布在1s附近。出现该现象的原因为，温度测量修正法利用装定信息同步阶段得到的时钟信息，减小了频率漂移的预测区间。该方法假设所有时钟的频率漂移测量结果均在图5.37（a）的边界范围内，而在实际情况下，部分时钟可能出现超出边界的频率漂移，导致部分时钟的实时校准结果误差偏大。

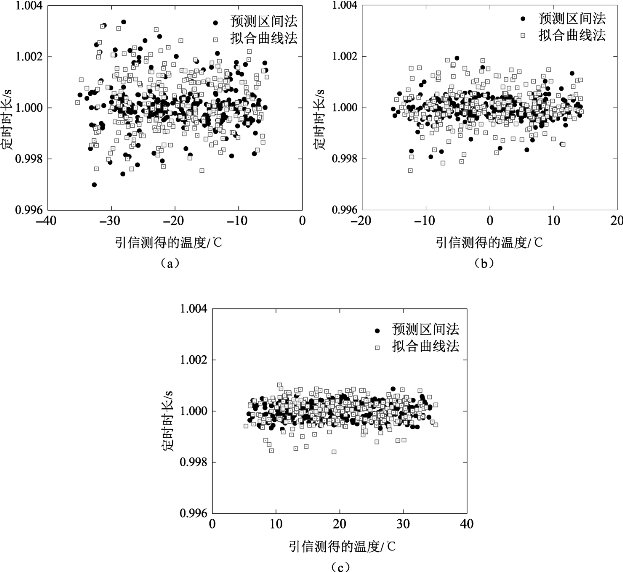
图5.38　变温度环境下引信时钟校正试验结果

（a）同步时温度为-20℃；（b）同步时温度为0℃；（c）同步时温度为20℃

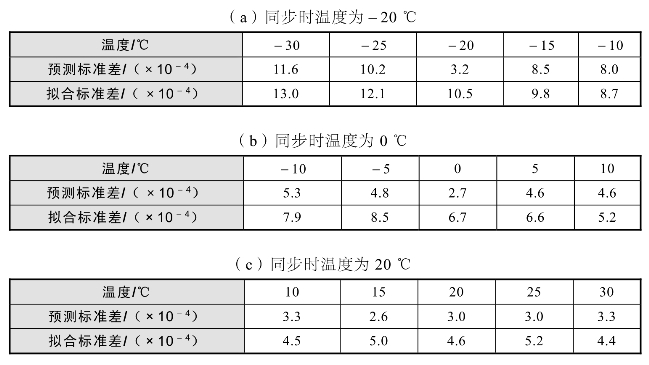
对图5.38中的数据进行了统计以定量对比本文所述两阶段时钟同步法和统计拟合法的同步效果，其结果见表5.6。表5.6列出了时钟不同温度、不同方法下的1s定时标准差。从表5.6中可以看出，装定信息同步法的时钟同步效果与温度无关，且效果远好于统计拟合修正法。温度跟踪法和统计拟合修正法与温度有关，温度跟踪法的标准差比拟合修正法小2 × 10-4s，从而验证了温度跟踪法优于统计拟合法。

表5.6　变温度环境下引信时钟校正试验统计结果

试验结果表明，如果不进行误差校正，引信在全温度范围内的基准频率标准差为2.35 kHz，在当前温度进行校正后频率标准差为0.20 kHz。采用统计拟合算法进行温度漂移校正的引信在±10℃范围内的基准频率标准差为1.38 kHz；采用温度探测算法进行温度漂移校正的引信在±10℃范围内的基准频率标准差为0.53 kHz；校正后的基准误差散布明显减小，且几乎不存在系统误差。(www.xing528.com)

探测和处理系统误差主要包括探测模型认知不确定性和探测基准误差两部分。由于探测系统基准与引信基准一致，在完成基准误差校正后，探测系统基准误差散布与处理器频率误差相同。为确定探测模型误差，进行了以下试验：第一，静态测量误差试验，给探测器输入用信号发生器模拟的被探测信号，测量探测器自身的误差；第二，动态测量误差试验，利用回收试验测量实际弹丸经过探测系统采集、处理系统解算得到的信息与多普勒雷达采集到的信息间的区别。

5.2.4.1　探测系统静态误差试验

试验方法为：第一，采用信号发生器分别输出幅值为0.1V、0.5V、1V和5V，频率为400Hz的正弦信号，输入到一个直径为35mm、匝数为200匝的圆形线圈中，以产生正弦磁场；第二，将探测器放置在距线圈中心50mm处，并接入引信系统中，观察探测系统的输出结果和处理系统的解算结果。试验结果如图5.39所示。其中，信号发生器输出幅值为0.1V时，比较器输出受噪声的影响很大，无法测出正弦信号的周期，信号发生器输出幅值为0.5V、1V和5V时，测得正弦信号分别为400.0Hz、399.9Hz和399.9Hz，误差很小。

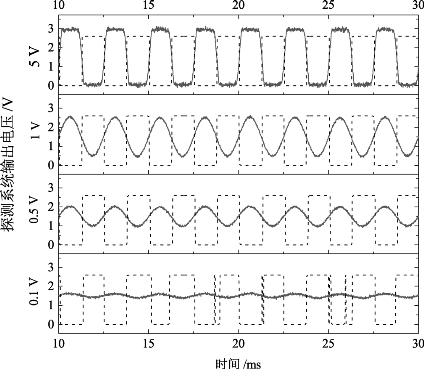
图5.39　探测系统静态输出波形

试验结果表明，当被测信号信噪比较小时，探测系统受噪声的影响很大，处理器无法得到正确结果；当被测信号信噪比较大时，探测系统静态误差约在10-4量级，静态误差对总误差的影响很小。

5.2.4.2　探测系统动态认知不确定性试验

试验方法为：按照弹药正常工作流程发射弹丸，在处理系统中增加信息采集和储存模块，记录探测系统采集到的信号和处理系统解算结果，回收弹丸后读取记录数据。试验共进行了两次，两次试验的引信搭载平台不同：第一次为阻力风帽弹丸的回收试验；第二次为圆锥风帽弹丸的回收试验。试验采集到的探测系统信号如图5.40所示。其中，传感器输入通过一个采样率为10 kHz的AD采样模块收集，比较器输出为处理系统通过内部比较器采集的传感器信号。在图5.40中，前10～20ms弹丸处于弹丸内弹道运动和后效期阶段，信号杂乱无章，无周期信号出现。当后效效应消失后，传感器采集到明显的周期信号，该信号的频率对应弹丸转速。在后效效应消失的一段时间内，周期信号的占空比不稳定，经过一定时长后，探测系统才能采集到稳定的周期信号。

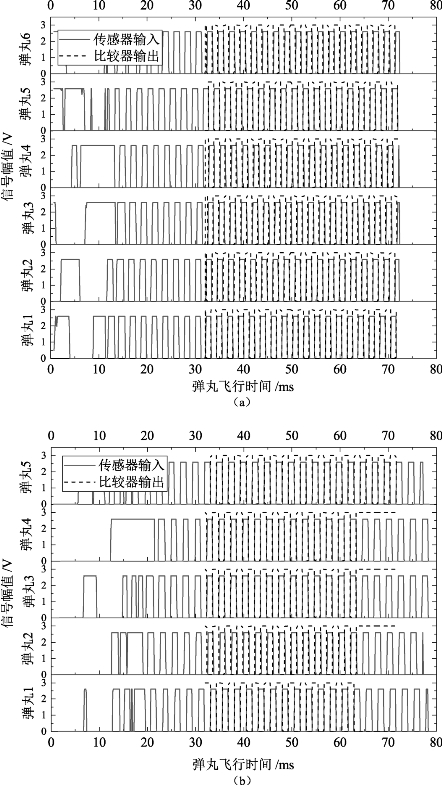
图5.40　回收试验采集到的探测系统信号

（a）阻力风帽弹丸；（b）圆锥风帽弹丸

处理系统根据探测系统采集到的周期信号解算弹丸初速，为了减小解算误差，探测系统采用32ms以后的周期信号作为解算输入，解算结果如表5.7所示。表5.7中，第一行为利用图5.40中比较器输出数据复原得到的信号频率，第二行为处理系统解算得到的弹丸转速，由于处理系统对比较器输出进行了基准误差校正，转速解算结果比信号频率约大2 r/s。以雷达测量初速作为基准，表5.7（a）中解算初速相对于雷达测量初速的误差均值为-0.7m/s，标准差为0.9m/s；表5.7（b）中解算初速相对于雷达测量初速的误差均值为-9.6m/s，标准差为0.7m/s。统计结果表明，初速解算的系统误差与弹形系数有关，需要针对不同弹形系数的弹丸分别校正。

表5.7　弹丸初速计算结果

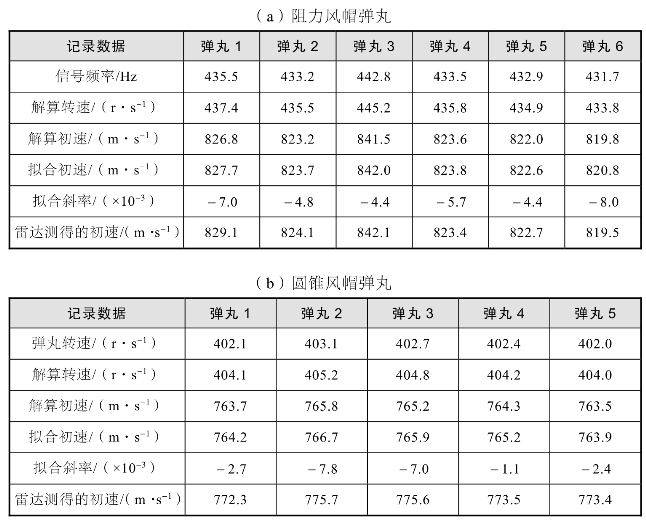
利用图5.40中的传感器输出信号，拟合弹丸在0时刻的转速，并换算成弹丸0时刻初速，拟合结果见表5.7。从拟合结果中可以看出，拟合初速与解算初速差距不显著，与雷达测得的初速依然差距较大。从拟合斜率中可以看出，弹丸转速呈下降趋势，但在置信度为0.95的条件下，拟合斜率与0的差别不显著。

试验结果表明，探测系统能够稳定地探测弹丸旋转信号，处理系统利用探测到的旋转信号能够解算出弹丸初速。用处理系统解算的弹丸初速和弹丸实际初速之间存在明显的系统误差，且该系统误差与弹形系数有关，对于圆锥风帽弹丸，以雷达测量初速为基准，其系统误差的统计结果为-9.6m/s，其随机误差较小，统计得到其标准差为0.7m/s，该误差无法通过将转速数据拟合至0时刻校正。