对于作用时间信息和修正系数信息等装定信息，若火控系统解算出的装定信息与目标和环境信息的相符度不高，则提高信息实时性并无意义。对于中大口径火炮所需的弹丸初速探测信息，若初速测量误差大于初速自身散布，则引入初速测量会带来反作用；对于计时基准信息，由于弹丸存在高过载环境，高精度晶体振荡器在引信中难以使用，而硅振荡器和RC振荡器存在出厂参数散布大、温度和时间漂移大、随机误差大等缺陷，极大地影响了动态控制系统的精准度；引信计时起点信息主要通过探测发射或碰目标过程中弹丸运动状态的变化得到，与火控系统解算中使用的理论计时起点不一致，同样导致控制系统精准度降低。这些误差可分为两组：一组是计时基准信息、计时起点信息和弹丸初速测量信息中与基准振荡器有关的部分，这组误差可称为控制基准误差；另一组是作用时间信息、修正系数信息和弹丸初速测量信息中与基准振荡器无关的部分，这一组误差可称为控制模型误差。
在信息处理技术中，可以通过时钟同步方法校准基准振荡器，从而校正基准误差。由于装定时间窗口限制，时钟同步占用的通信资源需要尽量小，且需要在仅进行一次同步的条件下保证整个控制系统过程的基准精准度，因此，我们采用两阶段时钟同步方法，该方法由装定信息同步和温度信息跟踪两个阶段组成，如图5.13所示。时钟同步所需要的输入包括：装定同步信息、装定过程中的初始温度信息和后续工作过程中的实时温度信息。时钟同步的输出结果为实时漂移α（t），时钟的实时输出结果t为：
式中，τ为时间积分变量；t0为计时起点。该方法的工作过程为：在装定信息同步阶段，引信利用装定信息估计控制基准的初始漂移并测量初始温度。在温度信息跟踪阶段，引信利用初始温度和初始漂移估计工作过程中的实时漂移，并按照实时漂移对其时钟进行自校准。
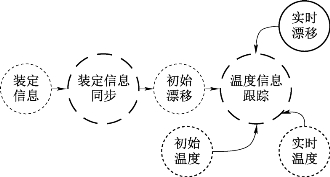
图5.13 控制误差校正原理
在处理技术中，我们提出了利用信息传输过程进行基准校正的方法，该方法仅需进行一次时钟同步，即可同时校正控制基准和计时起点，且在传输过程中不发送和接收绝对时间信息，占用通信资源很少。
设计了如图5.14所示的同步原理。该原理要求系统基带码型为带有时钟信息的定长码，一般基带码型均可满足该要求，为复原基带码型中的时钟信息，可在信源编码过程中插入等间隔符号。
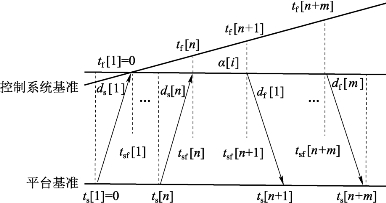
图5.14 双向伪时间戳时钟同步原理
在装定过程中，装定器共发送n个码元，引信共反馈m个码元，如图5.14所示。图5.14中，ts为装定器码元发送和接收时刻，tf为引信码元接收和发送时刻，tsf为采用装定器时钟度量的tf；ds[i]=tsf[i]-ts[i]，为装定延迟；df[i]=ts[i]-tsf[i]，为反馈延迟；α[i]=tf[i]/tsf[i]-1为单码元时钟漂移。装定信息同步阶段估计的参数为初始时钟漂移α（t0）。为进行温度信息跟踪，还需测量装定过程中引信的初始温度T0并估计时钟漂移预测区间p。
引信和装定器均无法直接获知tsf，因此，引信在接收第i个码元时的时钟漂移为：
式中，k为测量码元间隔。与TWTE方法不同，装定器发送的信息中不需要包含时间信息，不占用通信资源。为获知ts[i]-ts[i-k]，对于定长码，定义装定信息每个码元的长度均为τ，则时钟漂移的测量值αm[i]为：
αm[i]与α[i]的关系为：
式中，nsi为平台基准输出噪声；β[i]为装定器时钟漂移；nfi为控制系统检测噪声。
假设装定器经过良好校准，即E（β[i]）=0，则在整个装定过程中α（t0）的期望为：
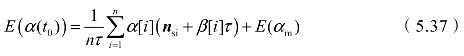
由式（5.37）可知，E（αm）是E（α（t0））的有偏估计，因此采用递归最小二乘滤波法估计α（t0），以减小估计误差。同时，为了减小预测区间p并简化计算过程，改进了递归最小二乘滤波法，使其能够在迭代过程中估计p。算法的更新过程如式（5.38）～式（5.42）所示。α的更新方法为：
式中，r为阶数；l为循环次数；λi为测量值的权重；λl=[λl+1-r，…，λn]，αml=[αm[l+1-r]，…，αm[l]]。λl的更新方法为：
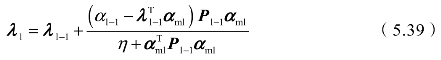
式中，η为遗忘系数；Pl为最小二乘系数矩阵，其更新方法为：
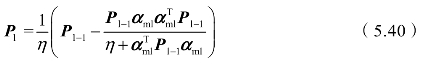
预测区间p更新方法为：
式中，标准差σl的更新方法为：
算法参数初始化为r=3，l=0，α0=0，λ0=0，P0=I/r，σ0=0，p0为：
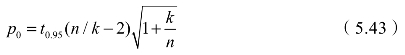
算法的迭代过程为：当l＜r时，l=l+1，αl=αm[（l-1）k+1]，pl通过式（5.41）和式（5.42）计算；当l≥r时采用式（5.38）～式（5.40）进行迭代。
为将计时起点出现时刻tus传输至引信，令ts[0]=0，tf[0]=0，则引信相对时钟起点为tus-ds[1]，只需计算出初始偏移量ds[1]，即可获得时钟起点。假设装定延迟的期望值与反馈延迟相同，且不随时间变化而变化，即E（ds）=E（df），则ds[1]的测量值dm[i]为：
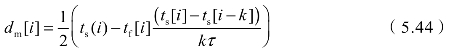
式中，i≥n+1。装定器无法直接获得tf[i]，传输tf[i]需要大量通信资源。引信在信息反馈时只向装定器发送一个数据tf[n+1]，则dm[i]为：
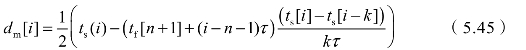(www.xing528.com)
式中，dm[i]与ds[1]的关系为：
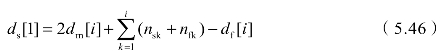
式中，dm[i]为ds[1]的无偏估计，初始延迟的估计结果为：
式中，M=（m+n+k+1）/2。在计算完成后，将tus-ds[1]传输给引信，即可让引信获知自身时钟起点。
根据表5.1所列参数对双向伪时间戳同步算法进行仿真，其中，α（t0）在仿真开始时随机产生。基准偏置的标准差和预测区间与计算所用同步码元数量的关系如图5.15所示，其中，每个k值均进行了2 000次仿真，统计当前k值下α（t0）测量结果与真实值的标准差和p的平均值。从中可以看出，当k=1b时α（t0）测量标准差及p均很大，随着k增大二者迅速减小，至k=3b时达到最小值，而后缓慢增大。均值法α（t0）测量结果标准差小于滤波法，但得到的预测区间更大。
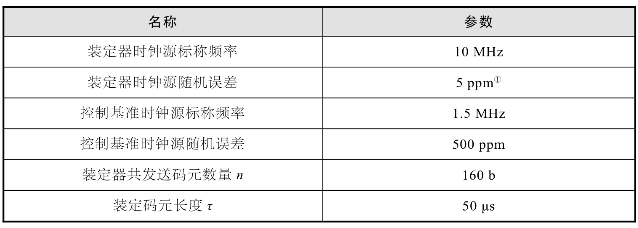
表5.1 时钟同步仿真参数
① 1 ppm=10-6。
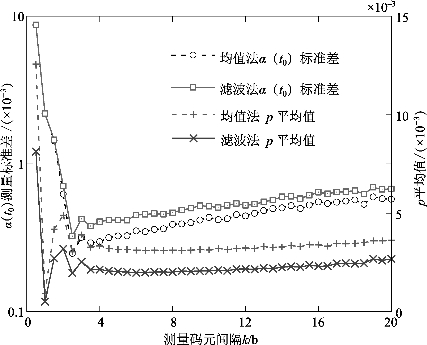
图5.15 同步码元间隔与基准偏置测量误差间的关系
图5.16展示了基准时钟在1s内的累计偏差值。当时钟源的随机误差标准差为500 ppm时，时钟同步效果受随机误差的影响很小，且校正后时钟累计偏差增长缓慢，1s处时钟累计偏差约为1.7 × 10-4s；当随机误差为5 000 ppm时，时钟同步效果受随机误差的影响很大，时钟同步结果不稳定，图5.16（b）中，均值法和滤波法均进行了两次仿真，由于随机误差的影响，两次仿真的结果差异很大，但均优于无校正的情况。从图5.16中可以得出结论，控制基准时钟源的随机误差对时钟同步结果影响很大，在实际使用中，需要为动态开环控制系统选用随机误差较小的时钟源。
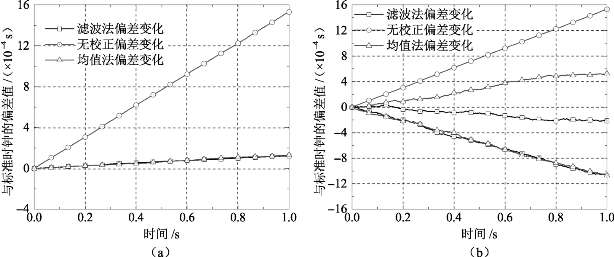
图5.16 1s定时区间内基准时钟的累计偏差值
（a）时钟源随机误差标准差为500ppm；（b）时钟源随机误差标准差为5 000 ppm
为满足时钟源随机误差约束，采用内部硅振荡器作为其时钟源，参数与表5.1一致。根据硅振荡器原理，引信时钟频率ffuze（T）随环境温度的变化函数为二次函数：
式中，Tb为基准温度；C1和C2为频率变化系数。由于振荡器参数的误差，各个控制基准的Tb、C1和C2不相同，无法直接采用式（5.48）计算不同温度下的时钟频率。
在对某批次的时钟源进行不同温度下时钟频率抽样测试后，得到温度-频率误差分布，如图5.17所示。其中时钟源的标称频率为1.5MHz，实线为拟合得到的二次曲线，虚线为预测区间。将式（5.48）转换为实际频率与标称频率的相对误差δ与温度的函数：
式中，β0、β1和β2为频率误差系数，令β=[β0，β1，β2]为系数矢量。频率相对误差与时钟漂移的关系为δ=-α。对于同批次的任意一个控制基准，β利用初始漂移、初始温度和式（5.49）预测。
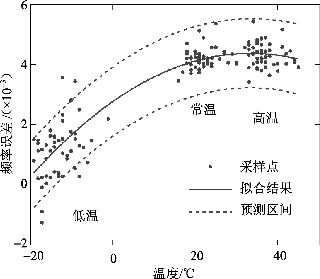
图5.17 频率误差相对于温度的变化采样结果
根据预测区间的定义可知，对于同批次的大多数时钟源，曲线［式（5.49）］上所有的点均位于预测区间内，且通过坐标为[TM，δ（TM）]的测量点M。因此，对于一个测量点M，所有可能的曲线为两条二次曲线围成的区间，这个区间可定义为优化问题：
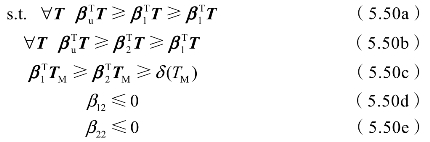
式中，β1和β2为两条边界曲线的参数，T=[1，T，T2]；为减少测量误差导致测量结果超出图5.17中上下界的情形发生，需要将曲线［式（5.49）］与预测区间p叠加，式（5.50a）和式（5.50b）中βu和βl为将p叠加入曲线［式（5.49）］后得到的预测区间上下界。式（5.50a）和式（5.50b）表示边界曲线上的所有点均在预测区间内，式（5.50c）表示两条边界曲线均需通过测量点M，式（5.50d）表示两条边界曲线均开口向下。式（5.50）为一非线性连续优化问题，为得到其最优解，将其离散化，并弱化其约束为优化问题：
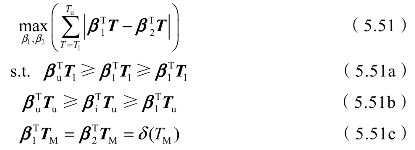
式中，i=1，2；式（5.51a）中Tl为温度最小值；式（5.51b）中Tu为温度最大值。式（5.51a）和式（5.51b）分别表示在温度最大值和最小值处的边界条件。显然，当β1满足方程：
β2满足方程：
时，优化问题式（5.51）达到最优。
由于优化问题式（5.51）是优化问题式（5.50）的约束弱化版，还需要判断得到的β1是否满足边界条件式（5.50a），β2是否满足边界条件式（5.50b）和式（5.50e）。若满足，则得到预测区间；若β2不满足式（5.50e），则令β22=0，代替式（5.52）中的一个方程，重新求解β2，得到的两个结果中必然有一个满足边界条件式（5.50b），以该结果作为新的β2。若β1不满足式（5.50a）或β2不满足式（5.50b），则计算β1与βl或β2与βu的距离最远的点Tc，若Tc＞Tm，则用Tl，Tm和Tc三个点求解得到新的β1或β2；若Tc＜Tm，则用Tc，Tm和Tu三个点求解得到新的β1或β2。
在测量温度分别为-40℃、-20℃、0℃、20℃和40℃时，仿真不同温度的频率漂移修正结果与实际温度的标准差如图5.18所示。其中，实线为利用测量结果修正的频率漂移（测量预测修正），虚线为利用统计期望直接修正的频率漂移（拟合曲线修正）。从图中可以看出，利用测量修正的频率漂移在多数情况下优于利用统计结果修正，随着实际温度远离被测量温度，修正结果趋近于统计结果修正。当温度测量结果处于20℃～40℃时，在当前测量结果附近能够获得接近测量结果的修正精度；当温度测量结果小于20℃时，修正偏差随着温度的下降而增大。
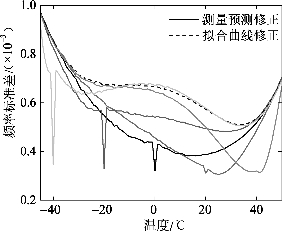
图5.18 测量预测修正与拟合曲线修正标准差对比
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
