膛内共线装定技术的基础理论

膛内装定技术是一种介于发射前装定和发射过程中装定之间的新型装定技术。相比于弹链装定和手工感应装定等其他发射前装定技术，膛内装定技术的信息实时性更好，能够对膛内已有弹药进行装定，相比于发射过程中装定技术和发射后装定技术，其具有不受环境干扰、能够为引信提供能源等优势。该技术根据是否对火炮炮闩进行改造，可以分为分线式膛内装定和底火共线式膛内装定两种。

分线式膛内装定技术最早出现于德国莱茵金属公司与美军合作对M256型滑膛炮的信息化改造项目，该火炮主要配用于西方主战坦克，如M1系列和豹2系列等。莱茵金属在2001年提出了坦克炮对空炸弹药的需求，并设计了坦克炮膛内信息传输方案，如图5.2所示。图5.2中，装定器通过坦克控制系统获取激光瞄具和火控计算机的信息，并通过炮闩装定给引信。

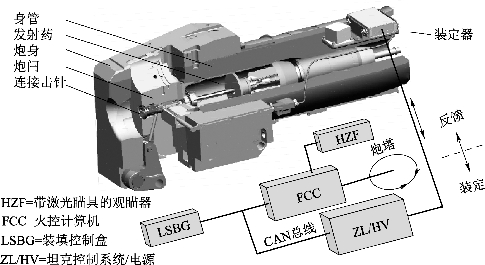
图5.2　膛内装定技术方案

图5.3　分线式膛内装定炮闩和弹药改造结构

（a）炮闩改造示意；（b）炮闩改造实物；（c）药筒改造示意；（d）药筒改造实物；（e）弹药内电气连接结构

为了保证弹丸在装定过程中不被击发，莱茵金属和美军对炮闩进行了改造，其中，莱茵金属公司设计了单向导通开关，如图5.3（a）所示。单向导通开关的一端连接底火发射击针，另一端连接信息装定接口，即图5.3（b）中北约接口。美军认为，莱茵金属所设计的方案存在信息传输速率限制等问题，所以重新对炮闩接口和通信协议进行了设计，在炮闩处增加了两个专门用于通信的触点，最终设计完成的炮闩同时兼容美军和德军两种协议，如图5.3（b）所示。美军还提供了信息化药筒的标准改造方案，在药筒底部嵌入数据转接电路板，通过电路板上的转接环与炮闩接口接触实现信息传输，如图5.3（c）和图5.3（d）所示。在弹药内部，信号通过缠绕在底火传火管上的软线和弹丸底部的插针传输进引信中，如图5.3（e）所示。

2008年美国通用动力公司提出针对105mm坦克炮的底火共线式膛内装定方案，其主要特点是对炮闩和药筒不做改造，信息直接通过原有火炮击发线传输，只需改造火控系统、底火和弹丸。装定系统从底火触点引出一根导线，接入弹头引信中，如图5.4（a）和图5.4（b）所示。以色列军工集团的APAM 120mm坦克炮弹药同样采用了底火共线式膛内装定方案，其弹药头部和底部分别有一个引信，通过底火中的切换开关单元选择引信或击发弹丸。

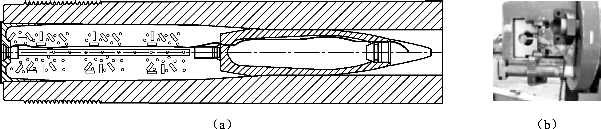
图5.4　底火共线式膛内装定结构

（a）底火共线式膛内装定示意；（b）火炮击发线

膛内共线装定系统的能量流和信息流包括：能量源到引信的能量储存能量流、信息源到引信信息接收的下行信息流和引信信息发送到装定器的上行信息流。因此需要建立装定系统的能量传输模型、下行信息传输模型和上行信息传输模型。装定系统所用信道可分为低通信道和带通信道，本节分别对低通信道和带通信道进行建模。

5.1.2.1　低通传输模型

低通传输模型如图5.5所示。装定器由功率放大器和功率限制器组成；引信能量接收系统由肖特基二极管和低通滤波器Cp组成；信息接收系统由低通滤波器Cs和解码器组成；Eavlb为直流恒压能量；X为信息源输入的码元符号序列。X中的码元分为两类，一类为供能码元Xp，该码元只有一个码元符号（在整个时钟周期内均为高电平），另外一类为信息码元Xs，分别计算二进制单极性码元和高斯码元的信道容量。

图5.5　低通传输模型框图

在分时分配法中：

式中，np为供能码元个数；ns为信息码元个数；np/（np+ns）=δt。在比例分配法中：

式中，ntotal为总码元个数。序列X通过功率限制器加载到传输特性为hs的低通信道上；因此，从低通信道输出的信息和能量同步传输信号为：

式中，sin（t）为以连续形式表示的X；Plmt=UlmtIlmt为功率限制器限制后的最大功率输出，Ulmt为电压上限，Ilmt为电流上限。为保证Plmt为最大输出功率，定义max{sin（t）}=1，与传统SPIT研究中{sin（t）}=1有所区别。

在接收端，信号被分为两股分别通过信息解码滤波器和能量接收滤波器。传输到解码器的信号为：

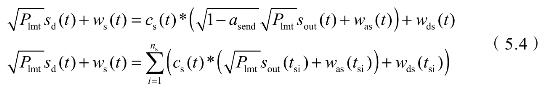
式中，cs（t）为信息解码滤波器传输函数；asend为功率分配系数；was（t）为接收端引入的信道噪声；wds（t）为解码器噪声；ws（t）为装定接收噪声：

当基带传输的信源输入为单极性二进制码元时，假定信道为二进制对称信道，则信道容量为：

式中，Xsi为X中的信息码元；Ysi为Y中的信息码元；Ss1为二进制码元中的一个码元符号；当噪声服从高斯分布时，p（Ysi=Ss1|Xsi=Ss1）为：

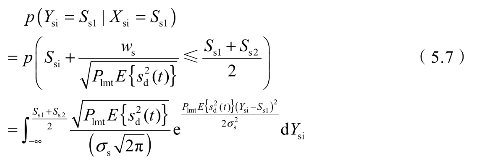
式中，Ss2为二进制码元中另一个码元符号，且Ss2＞Ss1；σs为装定接收噪声标准差；为解码器输入信号的期望。当基带信道为高斯白噪声信道时，信道容量为：

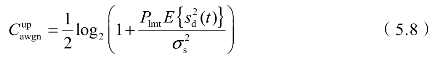
式（5.7）和式（5.8）确定了装定接收系统信道容量的边界。装定系统所发送的信息长度有限，且对每个引信只发送有限次数，无法满足式（5.7）和式（5.8）所要求的大编码长度，因此，需要求得特定的编码长度下的最优信息传输速率和最优编码长度。有限码长时，信息传输速率近似为：

式中，Vs为信道散布，该散布与噪声和编码长度有关；Φ-1（⋅）为取高斯分布分位数运算；ϵs为系统允许的最大误码率。对于对称二进制信道，信息传输速率为：

式中，pserror=1-P（Ysi=Ss1|Xsi=Ss1）为装定码元交叉概率。对于高斯信道，信息传输速率近似为：

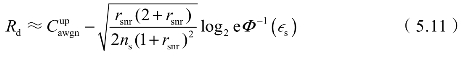
式中，rsnr=Plmt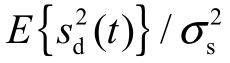为装定接收信噪比。

在图5.5中，能量接收系统通过肖特基二极管和滤波储能模块收集信道传输的能量，其中，信道中噪声的功率均值为0，无法被接收。由于功率限制器限制了系统的最大电流和最大电压，因此，传输到能量接收端的电压微分方程为：

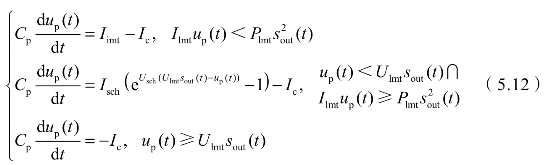
式中，Cp为低通滤波器滤波储能电容；Isch为肖特基二极管饱和电流；Usch为肖特基二极管热电压倒数，方程中Isch（e（Usch（⋅）-1））为肖特基二极管伏安特性曲线。方程（5.12）中，能量接收方程由三段组成：当充电功率Ilmtup（t）＜Plmt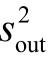（t）时，接收端以恒流Ilmt接收装定能量；当充电功率Ilmtup（t）≥Plmt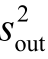（t）且接收端电压up（t）＜Ulmtsout（t）时，接收端以电压Ulmtsout（t）接收装定能量；当接收端电压up（t）≥Ulmtsout（t）时，只有系统能量消耗，而无装定能量接收。求解方程（5.12），得到接收端电压为：

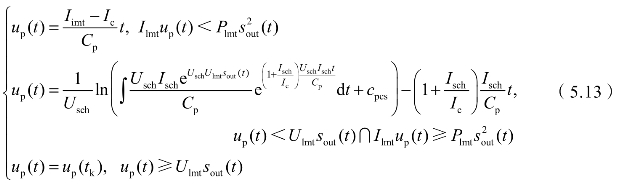
式中，cpcs为积分常数项，其结果由微分方程的边界条件决定；up（tk）为第k个状态切换时刻的电压值。方程（5.12）的边界条件为：up（0）=0，当发生状态切换时，两方程得到的结果相等。

基带反馈传输模型如图5.6所示。反馈信号Xf通过信号加载器加载到反馈信道上，并通过反馈信道传输到装定器端的反馈解码器上。由于系统反馈信道与装定信道相同hf（t）=hs（t），因此装定器收到的反馈信号为：

式中，Pf为加载反馈信息所消耗的平均功率；gf为信号加载器的低通特性；wf（t）为反馈噪声。与式（5.10）和式（5.11）相似，反馈信道的信息传输速率为：

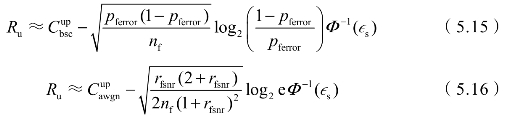
式中，pferror=1-P（Yfi=Sf1|Xfi=Sf1）为反馈码元交叉概率；nf为反馈码元个数；rfsnr=Pf/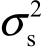为反馈信噪比。

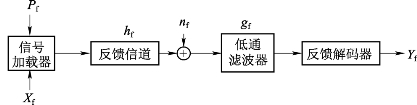
图5.6　反馈传输模型

5.1.2.2　带通信道传输系统模型

针对分装弹药无法采用有线连接作为传输信道的问题，设计了带通传输系统模型，如图5.7所示。带通传输系统的装定器端和引信接收端与基带传输系统相似，而信道部分除了低通传输线外还增加了无线传输天线。装定器输出到低通传输线上的信号为：

式中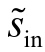，为复信道输入信号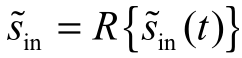，，R（·）为取实部运算；fc为带通信号载波频率。传输到引信接收端的复信号为：

式中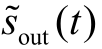，为复信道输入信号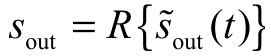，；hs1（t）为低通传输线信道特性；hs2（t）为带通传输线信道特性。

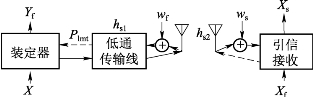
图5.7　带通传输系统模型(www.xing528.com)

在带通传输系统接收端，为了提高能量利用率，采用全波整流模块作为能量和信息接收方法，如图5.8所示。图5.8中，信号经过全波整流后被分成两股，分别进行能量接收和信息接收，而在图5.5中，低通信道能量接收与信息接收的分离发生在肖特基二极管整流之前。根据全波整流原理，通过整流器的带通实信号为。该信号通过低通滤波器Cp给储能模块供电，并通过带通滤波器Cs进行信息解调和解码接收。假定Cp和Cs均满足最优接收端功率分配条件，且带通信道为加性高斯白噪声信道。

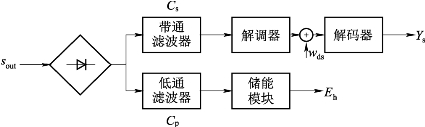
图5.8　带通模型能量和信息接收方法

当采用二进制编码时，其信息传输速率与式（5.10）相同，而码元正确传输概率变为：

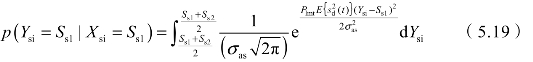
式中，σas→0；或：

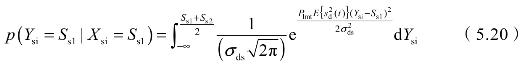
式中，σds→0。

当采用高斯编码时，其信息传输速率为：

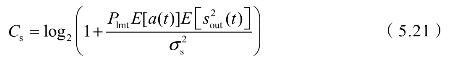
在带通模型中，由于发送端和接收端隔离，能量接收端以功率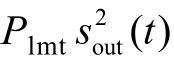的恒定功率接收装定能量，其充电微分方程为：

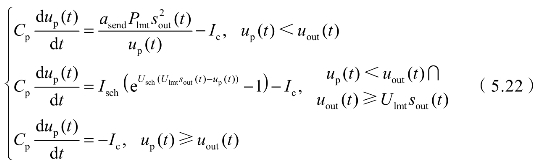
式中，uout（t）有：

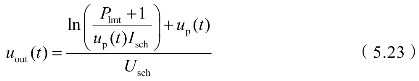
与式（5.13）相比，带通能量接收模型少了恒流充电过程，其接收到的总能量与式（5.14）相同。带通信息反馈与信息装定通过同一天线进行，信道为对称信道，则传输到反馈接收端的复信号为：

式中，为复信道反馈输入信号。反馈信道信息传输速率与式（5.15）和式（5.16）相同。

通过计算分析对比低通传输系统和带通传输系统的性能。首先，仿真分析二者的能量接收性能。仿真参数为：Ulmt=12V、Ilmt=0.05A、Cp=200μF、Ic=0.01A、hs1=1、hs2=1；肖特基二极管为BAT54系列，其参数为：Usch=26×10-3V-1、Isch=10-6A；带通传输系统能量传输频率为1MHz。图5.9展示了能量接收端电压与功率的仿真结果。图5.9中，低通传输系统采用恒电流传输，其储能模块电压线性上升。当asend=1时，在58ms处，能量传输转换为恒压模式，而后达到储能极限。带通传输系统为恒功率传输，电压累积速率随着电压上升而降低；当asend=1时，在50ms处，能量传输转换为恒压模式。当增加信息传输，且asend=0.5时，能量传输速率明显下降。

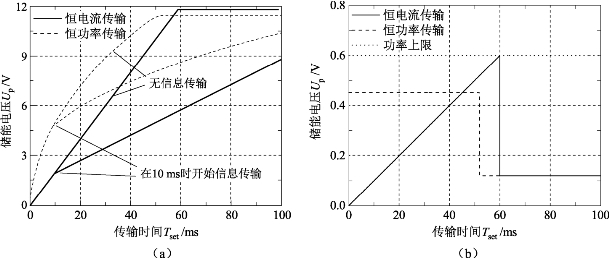
图5.9　能量接收端电压与功率仿真结果

（a）能量接收端电压变化曲线；（b）能量接收端功率变化曲线

从图5.9中可以得出结论，带通系统所使用的恒功率能量传输方法能够较为完全地利用传输到能量接收端的功率，而低通系统有部分功率被浪费，降低了能量传输效率，如图5.9（b）所示。图5.9（b）所示为充电过程中的平均功率变化。图5.9（b）中，低通模型只有在状态切换时刻达到最优功率；带通模型采用单一频率信号，平均功率维持在。只有在hs1=1及hs2=1的理想状态下，带通模型的能量传输速率才优于低通模型，事实上，无线传输信道必然存在功率损耗hs2=1不成立的情况，此时，带通模型劣于低通模型。

图5.10仿真了信道编码长度与信息传输速率间的关系。其仿真参数为：误码率为10-6、信噪比为5，其余仿真参数与能量接收仿真中相同。在图5.10中，不论低通信道还是带通信道均存在编码长度下界。当编码长度为100时，不论高斯信道模型还是二进制对称信道模型，均与当前误码率下的信息传输速率边界相差较远，且由于接收端结构有差异，带通传输系统的信息传输速率边界要小于低通传输系统。

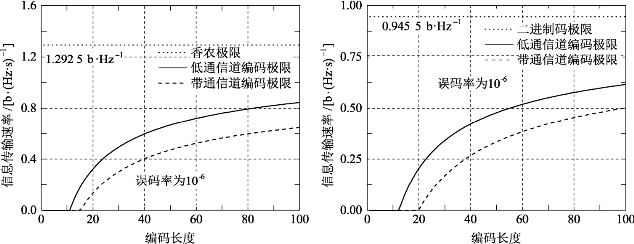
图5.10　信道编码长度与信息传输速率间的关系

（a）高斯信道模型；（b）二进制对称信道模型

从图5.10中可以看出，增加编码长度可以增加信息传输速率。然而，装定信息为定长信息，增加编码长度导致需传输的码元增多，且随着编码长度的增加，信息传输速率的增长变慢，因此，存在使信息的总传输时长最短的最优编码长度。假定信源信息的长度为ns0，则在编码长度ns≥ns0时，最短传输时长为：

式中，Bd为装定信道带宽；Rd为信息传输速率。根据式（5.10）和式（5.11），最优时长与ns、信噪比有关。不同信噪比下的最优编码长度和短传输时长如图5.11所示。图5.11中，信源编码后的装定信息长度为48b、信道带宽为100kHz。图5.11（a）表明，最优编码长度随着信噪比的增加而迅速降低，直至编码长度与信息总长度一致。图5.11（b）表明，在低信噪比条件下，低通模型信息传输时长显著小于带通模型，在高信噪比条件下，二者差别较小。当信噪比大于7.5dB时，采用高斯编码与二进制编码的差别不大。

根据图5.10，在相同信道条件下信道编码长度与信息传输速率间的关系保持不变。信息反馈传输与信息装定通过同一信道进行，因此，其信道编码长度规律与图5.10中低通信道曲线一致。同样，信息反馈传输的最优编码长度和最优传输时长如图5.12所示。图5.12中，信源编码后的反馈信息长度为8b。由于反馈信息的信息长度很短，当信噪比为10dB时，高斯编码的最优编码长度尚大于8b。图5.12（b）中，高斯编码曲线和二进制编码曲线出现交叉，在信噪比大于7.5dB时，二进制编码优于高斯编码。低通模型和带通模型曲线完全重合，信息反馈性能一致。

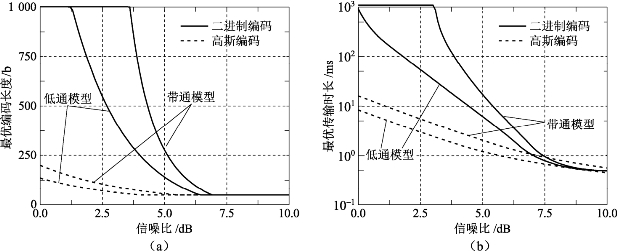
图5.11　最优编码长度与最短传输时长仿真结果

（a）最优编码长度；（b）最短传输时长

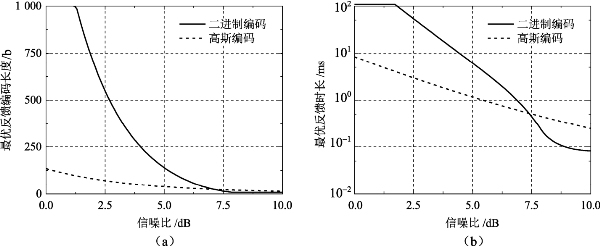
图5.12　最优反馈编码长度与最优反馈传输时长

（a）最优反馈编码长度；（b）最优反馈传输时长

根据上述仿真结果，在理想状况下，低通信道的能量传输性能比带通信道差，信息下行传输性能优于带通信道，二者反馈性能一致；若考虑信道特性，低通信道将显著优于带通信道，因此，最终选用低通信道传输系统作为装定系统的设计方案，且在实际应用场景中，信噪比较高，可采用二进制编码方案进行信道编码。

共线装定系统共用底火回路进行信息交联。装定过程和发射过程的相互影响会导致装定失败和弹丸意外发射等异常情况，我们将这种相互影响称为能量流串扰，需要对能量流串扰进行抑制。

理想能量流串扰抑制效果为η1=[1，0]、η2=[0，1]，此时，能量流串扰完全消失。然而，达到该理想效果所需的成本过高，因此，需要寻求一种容易达到的能量流串扰抑制边界条件。

假设装定控制器的能量输出无法对击发系统产生影响，串扰抑制边界条件为：

1）在回路中未出现发射能量时，底火桥丝上的温度累积应当小于发火所需温度：

式中，αs＜1为装定能量流抑制安全系数。

2）当发射能量出现在回路中时，底火桥丝上的温度最大值应当大于可靠发火温度，且维持一段时间：

式中，tl和tu为桥丝温度超过可靠发火温度时间的下界和上界。

3）到达装定接收系统的瞬时功率应当小于引信最大安全输入功率：

式中，Pl2为引信最大允许输入功率；Pt2为装定接收端的瞬时功率。

4）到达装定接收系统的能量大于引信最小需求能量：

式中，tr为弹丸实际发射时刻。

5）通过能量限制器的瞬时功率不能大于底火发火系统的最大安全功率：

式中，Pa为发火系统最大安全功率；Pt1为底火桥丝上的瞬时功率。

6）能量无法从发射能量源流入装定控制器：

式中，当能量流入装定控制器时Ps2为负；Ps2为装定能量源的瞬时功率。

能量流串扰抑制系统的边界条件为：

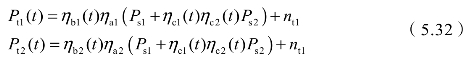
式中，ηa1和ηa2为线路损耗及功率分配系数；ηb1（t）为发射串扰抑制系数；ηb2（t）为装定串扰抑制系数；ηc1（t）和ηc2（t）为能量限制系数。