引信自测速时间修正技术优化方案

引信自测速时间修正思想是装定器给引信装定的、未经修正的作用时间。弹丸发射后，引信自动测量弹丸的速度，并对装定的飞行时间进行修正。如图4.25所示，虚线表示的是弹丸以标准初速v0发射时的理想弹道，M0为t0作用时间的炸点，即理想炸点。实线表示的是弹丸以实际初速v1发射时的实际弹道，由于初速的偏差导致两条弹道之间产生偏离，当v1＜v0时，实际弹道位于理想弹道下方。在弹丸实际飞行时间为t0时，炸点为M，实际炸点斜距离小于理想炸点的斜距离。由于弹丸发射后，各种射击诸元已不可能进行改变，因此实际弹道与理想弹道的偏离是不可避免的，也就是说，不可能将实际炸点M修正到理想炸点M0的位置。对于防空反导弹药来讲，炸点修正的原则应该是等斜距离修正，即将炸点修正到与离炮位的距离与理想炸点相等的M1点，以利于对低空飞机、巡航导弹等目标的拦截。

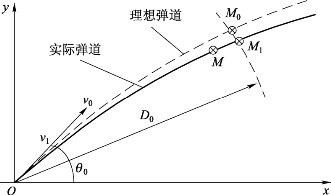
图4.25　时间修正方法示意

在基本假设条件下，当c、v0、θ0给定时，弹丸的质心在空中的运动轨迹只有一条，且唯一地由初始条件和下列方程完全确定：

由于H（y）和F（v）是用数值表或经验公式表示的复杂函数，所以对上述方程进行积分时得不到精确的解析式，故只能用数值积分的方法求其数值解。(www.xing528.com)

但是，引信中不具备上述方程中的所有初始条件，如θ0和气象条件等，所以求解这一方程是困难的。在初速误差不是很大时，由于其射击诸元是完全一致的，其气象条件也完全一样，所以两条弹道的偏离很小。可假设两弹道的H（y）和F（v）近似相等，因此两弹道的唯一差别是初速不同，弹道具有相似性，可假设两条弹道上对应点的速度的比值和方向保持不变：

这样，在斜射距一定时，其飞行时间和初速成反比，所以可按下式对作用时间进行修正：

式中，t为修正后的弹丸飞行到M1点所需的飞行时间；v是弹丸的实际初速，在弹丸出炮口时由装定器或引信自身测得；t0是弹丸以标准初速v0飞行到理想炸点所需的时间，可以从弹道计算机获得。