引信作用时间修正技术优化

引信测得炮口速度后，要根据所测速度与理论速度的关系，对引信作用时间进行修正，而如何由弹目距离、射表以及测得的炮口速度得到实际定时时间来达到理想炸点效果，则需对作用时间修正技术进行研究。

3.4.1.1　弹道描述

在弹道修正计算分析时，由于单兵火箭弹丸的射程误差远大于方向误差，故忽略弹丸方向误差，只考虑射程误差。假设弹道在射击平面内，S0为时间t0时理想空炸炸点位置，由于弹丸的初速误差等因素的存在，实际弹道和理想弹道是不重合的，弹道示意如图3.21所示，名义弹道0即弹丸的理想轨迹，实际弹道1为初速v1＞v0的实际弹道，实际弹道2为初速v2＜v0的实际弹道。

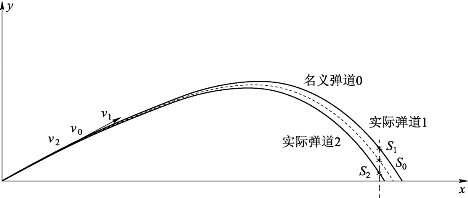
图3.21　弹道示意

在初速误差不是很大时，由于其射击诸元是完全一致的，气象条件也完全一致，所以两条弹道的偏离也很小，那么名义弹道与实际弹道的唯一区别就是初速不同。由于在弹丸发射后，不可能把炸点S修正到目标位置S0处，所以可根据目标的最优毁伤效果，选择等射距、等炸高、等射程三种修正原则对炸点进行修正。本书采用等射程的修正原则对炸点位置进行修正，以达到提高炸点精度的目的，S1、S2分别为实际弹道修正后的空炸炸点位置。由于引信中不具备弹道方程中的所有初始条件，所以要解弹道方程是困难的，引信只能根据弹丸的理论速度v0、发射平台装定给引信的作用时间t0和作用距离X、引信测得的弹丸的实测速度v等参数计算引信的实际作用时间t。

3.4.1.2　指数规律修正方法

根据弹道方程，若将质点弹道近似为平面弹道，并将弹丸受到的升力、马格纳斯力、科氏力取为0，则：

式中，Sm表示弹丸最大横断面面积，本算例中取为5.024×10-3m2；ρ表示空气密度，ρ=1.293kg/m3；Cx表示阻力系数，取0.45；m表示弹丸质量，取1.645 33kg；θ1表示弹道倾角；ψ2表示弹道偏角；相对于弹速v，风速v‖较小，可以忽略。故上式可转换为

变换为以弹丸飞行距离s为自变量的质点弹道方程的切向方程：

由于单兵火箭弹运动弹道属于低伸弹道，且射程较短，所以可近似认为射程X与弹道弧度s相等，当θ1＜100时，得到射程X修正公式：

式中，d为附加的修正项，当理论初速v0=172m/s时，拟合度为95%，得到d=-4.975，则修正后弹丸实际作用时间为：

3.4.1.3　反比例修正方法

由于弹道具有相似性，可假设弹道上对应点速度的比值和方向不变，那么在射程一定时，其飞行时间和初速成反比，可用式（3.29）对引信作用时间修正。

(www.xing528.com)

式（3.29）中，v0为弹丸理论初速；v′为弹丸实测初速；t0为引信理论初速时弹丸飞行时间；t为修正后弹丸飞行时间；Δt为修正公式中引入的修正项。

在速度散布155～180m/s范围内，θ1=7.091°，D=600m时，Δt的取值范围为0.000 2～0.000 5s；θ1=5.7°，D=500m时，Δt的取值范围为0.000 1～0.000 9s；θ1=4.406°，D=400m时，Δt的取值范围为0.000 2～0.000 8s，因此Δt均在±1ms以内，修正时可以忽略，即将修正公式改写为式（3.30），修正后的结果仍可达到很高的精度。

3.4.1.4　平均速度修正方法

弹丸运动时的射程随时间几乎成线性变化，所以可近似认为弹丸的平均速度乘上飞行时间等于射程。当弹丸自测速系统测得弹丸实际速度时，根据射程相等的原则，用弹丸的飞行时间与平均速度的倒数成正比进行修正，修正公式为式（3.31）。引信根据修正后的飞行时间点爆弹丸，从而实现精确击中目标。

式中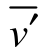，表示实测平均速度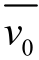；表示理论平均速度。

假设X表示射程，那么

而

将式（3.32）和式（3.33）带入式（3.31）可得

3.4.1.5　修正方法的比较

弹丸射程的射角以插值的方式得到，火箭弹发射时的初速是设计初速，可得到一系列火箭弹的实际飞行轨迹，以三种修正方法对引信作用时间修正后的时间作为弹丸飞行时间的终止条件，从而得到弹丸经过作用时间修正后的实际炸点位置，与目标位置比较即可得到经过时间修正后的炸点误差。

图3.22（a）所示为初速为165m/s时三种修正方法修正精度随射程变化的拟合曲线，它表明以指数规律修正方法修正的精度曲线随着射程的增加而曲折变化，变化幅度较大，在600m位置处误差达到13.564m，以反比例关系修正方法修正的精度曲线一直平缓地保持很小的值，以平均速度修正方法修正的精度随着射程的增加而近似呈线性比例增加，修正误差始终为正值，在600m位置处误差达到7.516m；图3.22（b）所示为初速为175m/s时三种修正方法修正精度随射程变化的拟合曲线，它表明以指数规律修正方法修正的精度曲线随着射程的增加而曲折变化，在600m位置处误差达到13.623m，以反比例关系修正方法修正的精度曲线一直平缓地保持很小的值，以平均速度修正方法修正的精度随着射程的增加而近乎呈线性比例增加，修正误差始终为负值，在600m位置处误差达到-2.969m。从仿真结果得出修正方法的修正精度由高到低依次为：反比例修正方法、平均速度修正方法、指数规律修正方法。

图3.22　不同初速变化时以三种修正方法修正的误差随射程变化的曲线

（a）初速变化为-5m/s时修正误差随射程变化的曲线；（b）初速变化为+5m/s时修正误差随射程变化的曲线