1.交流同步电动机的双轴理论基础
双轴理论的基本思想是:在产生相同的旋转磁场并保持功率不变这一等效原则下,将交流电动机的三相绕组A、B、C与两个正交并以同步转速旋转的直流绕组d、q相等效,从而将三相交流量变换为d-q坐标系下的直流量。在此基础上即可仿照直流电动机来对交流电动机的动态性能进行分析,并实现对电磁转矩的快速精确控制,从而使交流电动机达到与直流电动机相同的动态性能。
等效变换是双轴理论的重要基础。等效变换的第一步是将三相交流绕组等效为二相交流绕组,由此实现三相交流量到二相交流量的变换。
由电机学原理可知,对称的二相、三相、四相等多相绕组通以对应的多相平衡正弦交流电流后,将产生转速为ω的旋转磁场Φ。图2-14a是三相绕组通以三相交流电流产生的旋转磁场,图2-14b是二相绕组通以二相交流电流产生的旋转磁场。如果旋转磁场的大小和转速都相等,则这两套绕组等效。
根据磁动势相等原则,三相坐标系下磁动势分量与二相坐标系下磁动势分量有以下关系:
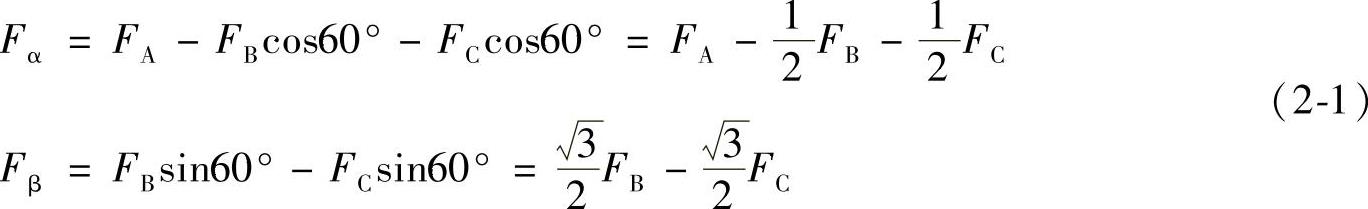
式中,FA、FB、FC是三相坐标系下磁动势分量;Fα、Fβ是二相坐标系下磁动势分量。
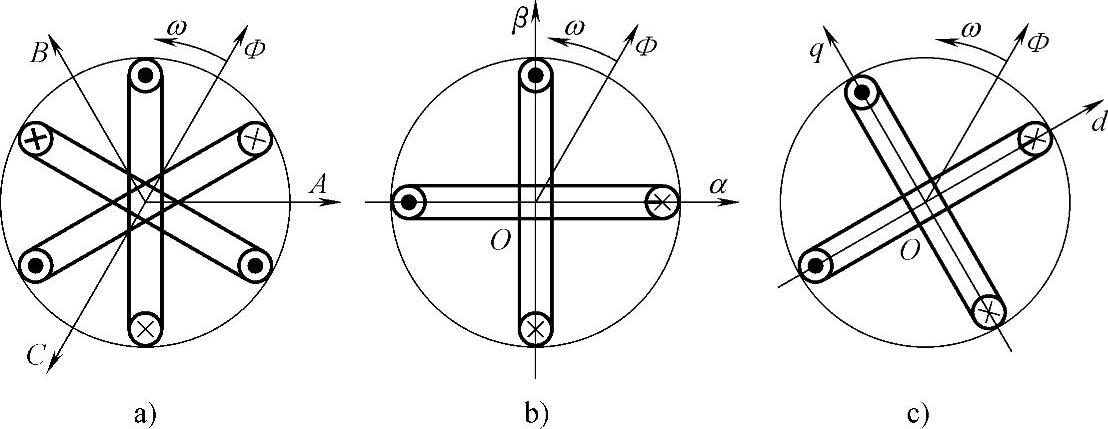
图2-14 三相电动机的等效绕组
通过归算可将磁动势关系转换为电流关系:
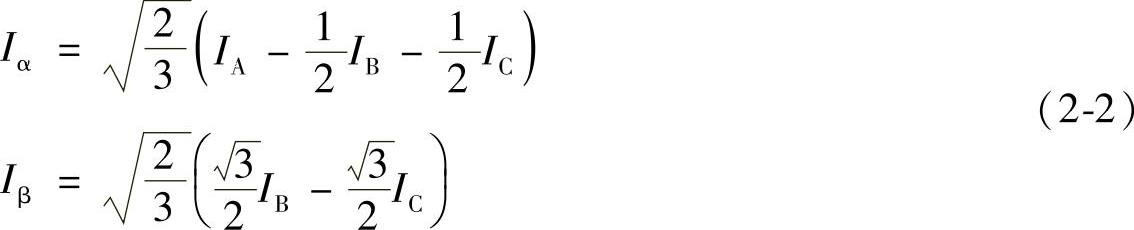
式中,IA、IB、IC是三相电流;Iα、Iβ是二相电流。
写成矩阵形式为
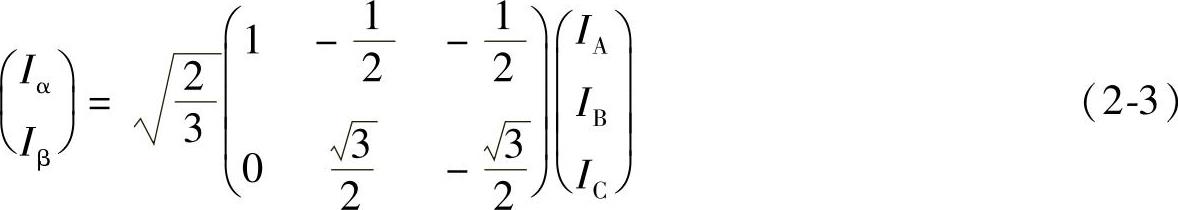
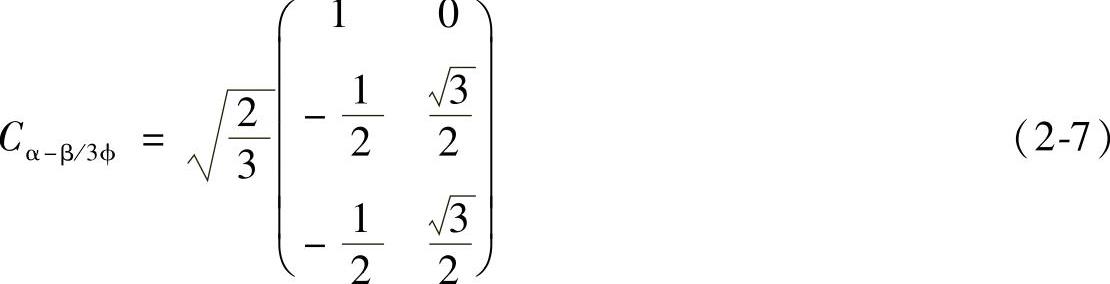
由此可得三相A-B-C坐标系到二相α-β坐标系的变换矩阵

在以上3ϕ/α-β变换的基础上,再将二相交流绕组等效为旋转坐标系下的正交直流绕组d、q,如图2-14c所示,由此可导出二相交流量到正交直流量的变换矩阵:

式中,φ是磁通位置角,即磁通Φ与A轴或α轴的夹角。
同理,可得到正交直流量到二相交流量的逆变换矩阵为

以及二相交流量到三相交流量的逆变换矩阵
2.d-q坐标系下交流同步电动机的数学模型
d-q坐标系下同步电动机的基本模型如图2-15所示。从驱动控制的角度看,交流同步电动机在d-q坐标系下的数学模型主要包括以下方程。
(1)磁链方程
选择d轴正方向与转子永磁励磁磁链方向一致,得永磁同步电动机磁链方程:

式中,ψf是永磁励磁磁链;ψd、ψq是d轴和q轴磁链;Ld、Lq是d轴和q轴电感;Id、Iq是d轴和q轴电流。
(2)电压平衡方程
因为用于伺服驱动的同步电动机的转子上无绕组,仅列出定子回路的电压平衡方程:

式中,Ud、Uq是d轴和q轴电压;R是定子相电阻;ωr是转子角速度。
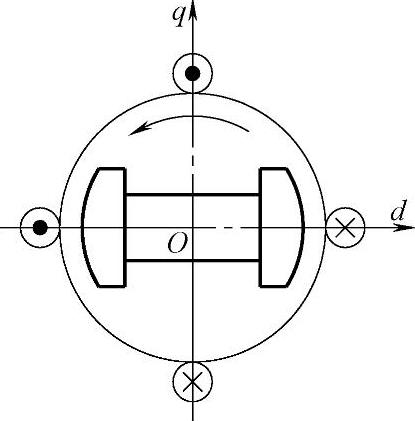
图2-15 d-q坐标系下 同步电动机模型
(3)电磁转矩公式
在d-q坐标系下,交流永磁同步电动机电磁转矩公式如下
T=K(ψdIq-ψqId)(2-10)
式中,K是由电动机结构确定的常数。
将磁链方程(2-8)代入式(2-10)有
T=K[ψfIq+(Ld-Lq)IdIq](2-11)
(4)转矩平衡方程

式中,θ是电动机转角;J是转动惯量;C是速度阻尼系数;TL是负载转矩。
3.d-q坐标系下交流异步电动机的数学模型
d-q坐标系下异步电动机的基本模型如图2-16所示。从驱动控制的角度看,交流异步电动机在d-q坐标系下的数学模型主要包括以下方程。
(1)磁链方程
变换到d-q坐标系后,异步电动机定子回路有d、q两个绕组,转子回路也有d、q两个绕组。因此,在d-q坐标系下,异步电动机的磁链方程组包括以下4个方程
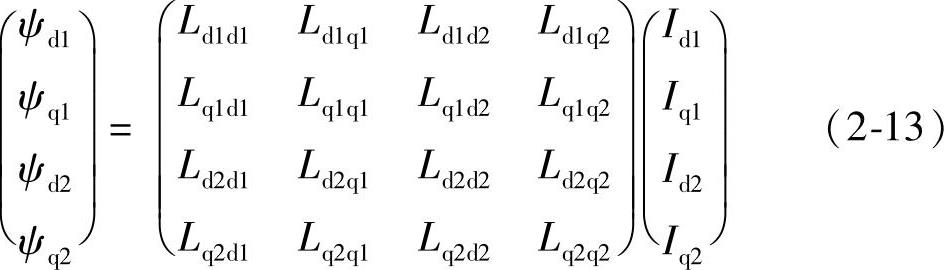
式中,ψd1、ψq1是定子d、q轴磁链;ψd2、ψq2是转子d、q轴磁链;Id1、Iq1是定子d、q轴电流;Id2、Iq2是转子d、q轴电流。
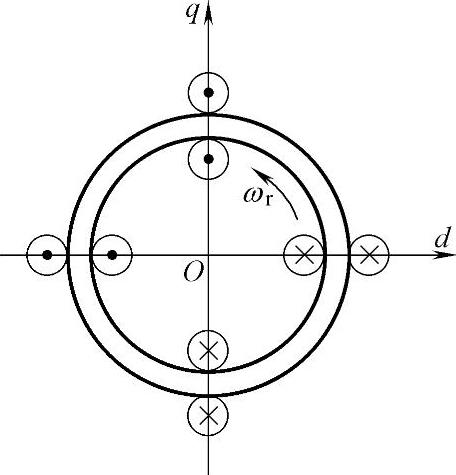
图2-16 d-q坐标系下异步电动机模型
Ld1d1、Lq1q1:定子d、q轴绕组自感,因两轴对称其值相等,简记为L1。
Ld2d2、Lq2q2:转子d、q轴绕组自感,因两轴对称其值相等,简记为L2。
Ld1q1、Lq1d1:定子d、q轴绕组间互感,因两轴位置固定且相互垂直,其值为0。
Ld2q2、Lq2d2:转子d、q轴绕组间互感,因两轴位置固定且相互垂直,其值为0。
设LM为定转子绕组间互感的最大值,θ为定转子绕组轴线间的夹角,则:
Ld1d2=Ld2d1=LMcosθ:定转子d轴绕组间的互感,因两轴夹角θ=0°,其值为LM。
Lq1q2=Lq2q1=LMcosθ:定转子q轴绕组间的互感,因两轴夹角θ=0°,其值为LM。
Ld1q2=Lq2d1=LMcosθ:定转子d、q轴绕组间的互感,因两轴夹角θ=90°,其值为0。
Lq1d2=Ld2q1=LMcosθ:定转子d、q轴绕组间的互感,因两轴夹角θ=90°,其值为0。
根据以上分析,磁链方程可进一步表示为
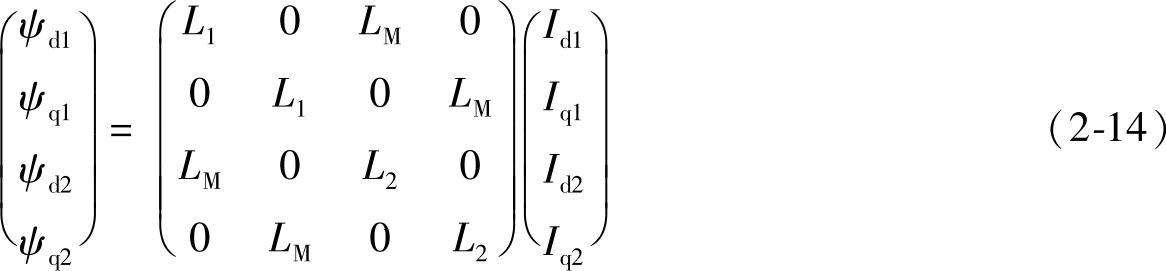
简记为:
Ψ=LI(2-15)
式中,ψ、L、I分别是磁链、电感和电流矩阵。
(2)电压平衡方程
异步电动机的电压平衡方程组包括如下4个方程

式中,Ud1、Uq1是定子d、q轴电压;R1、R2是定、转子电阻;ω1是定子旋转磁场角速度;ωS是转差角速度;P是微分算子,P=d/dt。
(3)电磁转矩公式
考虑磁场储能
 (https://www.xing528.com)
(https://www.xing528.com)
电磁转矩公式可表示为

式中,θ是转子绕组轴线与定子绕组轴线间的夹角。
因
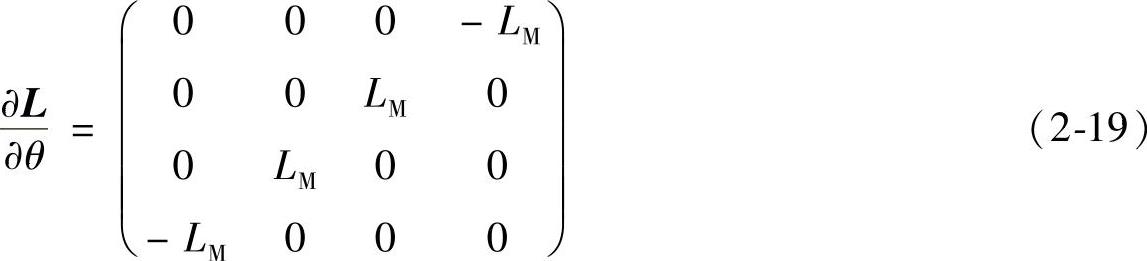
代入式(2-18)得

(4)转矩平衡方程

式中,θ是电动机转角;J是转动惯量;C是速度阻尼系数;TL是负载转矩。
4.交流同步伺服进给驱动系统
由d-q坐标系下同步电动机的数学模型可知,在磁场定向(永磁励磁磁链方向与d轴正方向一致)的前提下,永磁同步电动机的电磁转矩公式为
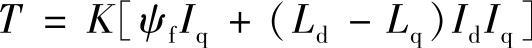
从上式可以看到,如果通过电流控制使d轴电流Id=0,则有

由于永磁励磁磁链ψf为常数,因此,此时电动机输出的电磁转矩将与q轴电流Iq成正比。这意味着控制Iq就可以像控制直流伺服电动机一样实现对交流永磁同步电动机电磁转矩的直接控制。
实现这种模拟直流电动机控制的前提是磁场定向,即必须保证永磁励磁磁链ψf的方向与d轴方向一致(见图2-17)。为实现这一要求,可通过安装于电动机轴上的转子位置传感器(如,编码盘、旋转变压器等)实时获取以θr角表示的转子磁极位置信息。显然,如果θr检测有误差,将不能保证ψf的方向与d轴方向一致,从而使定子电流Is在ψf方向的投影不等于零,控制效果达不到理想境界。

图2-17 磁场定向 控制示意图
由上可知,在磁场定向的基础上,要准确控制永磁交流同步电动机的电磁转矩,就必须在d-q坐标系中对定子电流Id和Iq进行有效控制,即保证Id恒为0的同时,使Iq等于由希望电磁转矩确定的指令值。考虑到驱动系统运行过程中不可避免存在各种干扰,因此,为抑制这些干扰的影响,保证电流控制的准确性,对Id和Iq的控制必须通过闭环方式进行。
由于d-q坐标系下的Id和Iq与三相交流坐标系下的电流IA、IB、IC间存在确定的坐标变换关系,因此,进行电流闭环控制时可采用两种方案来实现:一种为直流闭环控制方案,另一种为交流闭环控制方案。
直流闭环控制的基本思想是在变换后的d-q坐标系中,对电流Id和Iq分别进行闭环控制,从而实现对电磁转矩的直接控制。由于在d-q坐标系中,电流Id和Iq均为直流量,因此,称为直流闭环控制。按该方案构成的电磁转矩控制系统的基本结构如图2-18所示。图中右上角带*表示指令值,下同。

图2-18 直流闭环电磁转矩控制系统
交流闭环控制的基本思想是在A-B-C坐标系中,对电流IA、IB、IC分别进行闭环控制,从而实现对电磁转矩的直接控制。由于在A-B-C坐标系中,电流IA、IB、IC均为交流量,因此,称为交流闭环控制。按该方案构成的电磁转矩控制系统的基本结构如图2-19所示。
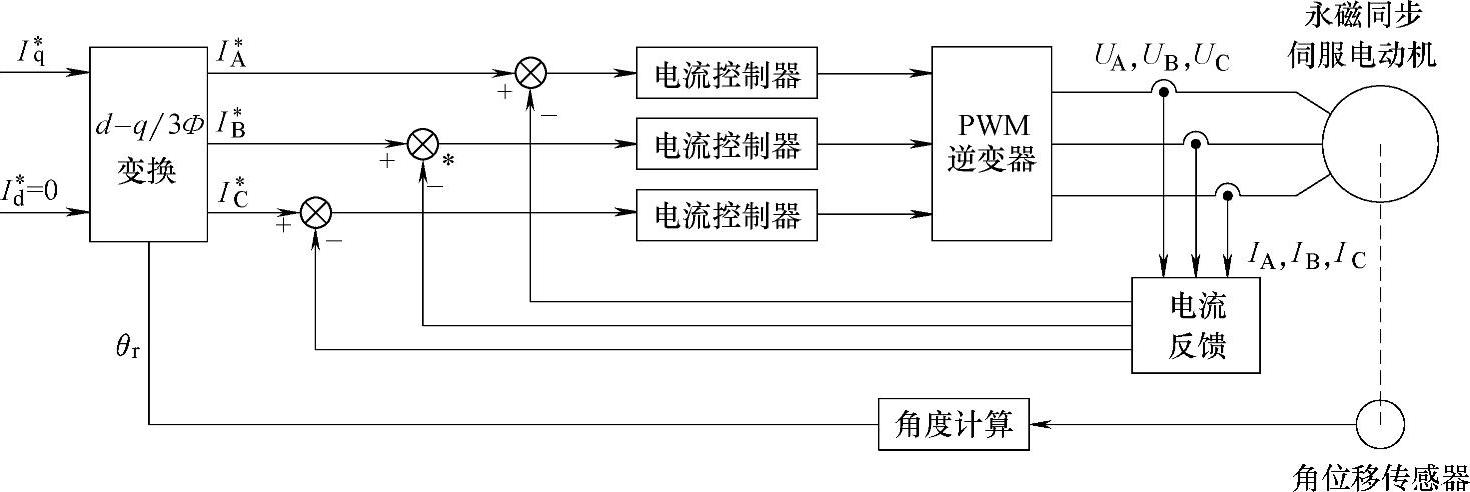
图2-19 交流闭环电磁转矩控制系统
在对永磁同步电动机进行电流(电磁转矩)控制的基础上,可进一步构成速度与位置控制系统,如图2-20所示。该系统的速度控制环以上述电磁转矩控制系统和电动机为被控对象,通过检测装置获取电动机的实际旋转速度,实现对电动机转速的快速准确控制。该系统的外环为位置控制环,它以整个速度内环为被控对象,通过编码器等检测装置获取电动机实际转角信息,最终实现对电动机角位移的精确快速控制。
5.交流异步伺服主轴驱动系统
与进给伺服驱动系统不同,主轴驱动系统不仅要求有较强的位置控制能力,以实现主轴定向准停和联动控制功能,而且还要求具有很高的速度控制能力,以实现具有高转速上限的宽范围恒功率调速。为此,基于异步电动机的交流主轴驱动系统必须重点解决“高速”和“弱磁”控制两个关键问题。
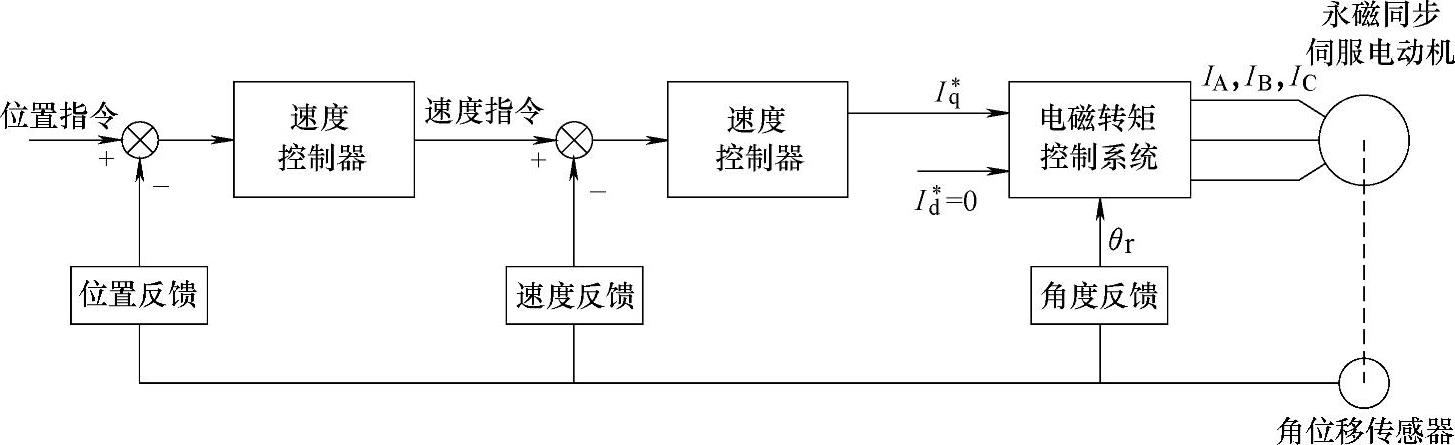
图2-20 永磁同步电动机伺服驱动系统
(1)高速情况下转子磁链的求解方法
通过磁链求解,得到转子磁链的位置角θ,是实现异步电动机矢量变换控制的关键。由于主轴电动机转速比进给电动机高得多,如果仍然采用进给驱动系统的磁链求解方法,则在高速下容易产生振荡,并且由于对转子电阻变化敏感性很强,难以保证精度。为此,在主轴驱动系统的矢量变换控制中可采用下面介绍的求解转子磁链的电压模型。
在α-β坐标系下,异步电动机的电压平衡方程为
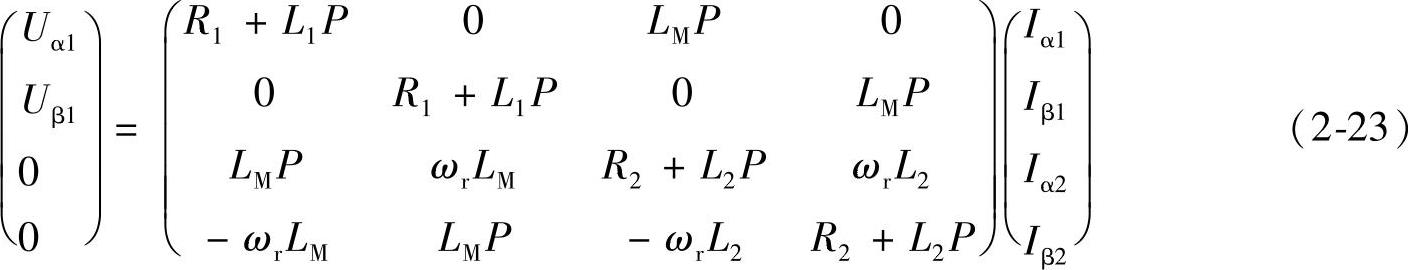
α、β轴转子磁链方程为

从式(2-24)可解出:

将式(2-25)代入式(2-23)中,可得:
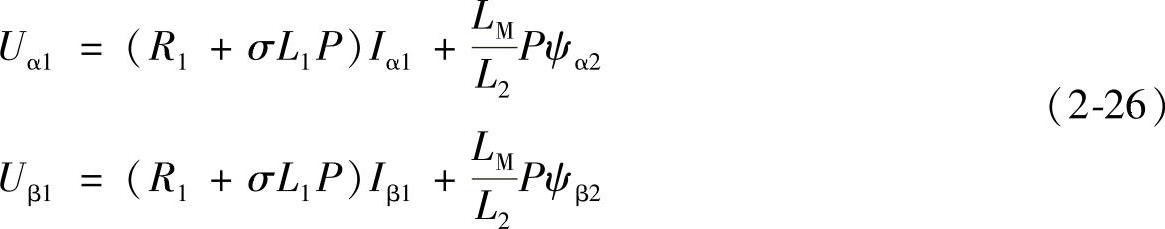
式中,σ=1-L2M/(L1L2)。
解方程(2-26)求出ψα2、ψβ2后,即可求出转子磁链ψ2的位置角。
θ=arctan(ψβ2/ψα2)(2-27)
(2)满足恒功率调速要求的弱磁控制
为实现异步电动机的恒功率调速,必须采取类似于他励直流电动机的弱磁控制方法。为此,需在矢量变换控制系统中设置变磁链(磁通)给定环节,其磁链变化曲线如图2-21所示。在额定转速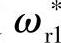 以下,磁链
以下,磁链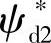 保持恒定,实现恒转矩调速。在额定转速
保持恒定,实现恒转矩调速。在额定转速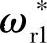 以上,磁链
以上,磁链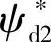 按照图中弱磁曲线变化,实现恒功率调速。
按照图中弱磁曲线变化,实现恒功率调速。
通过上述磁链给定环节得到磁链指令值后,可采用直接或间接控制方法对实际磁链进行控制。直接控制是通过获取实际磁链(磁通)反馈值,以闭环方式对实际磁链进行直接控制。间接控制是通过将磁链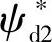 转化为d轴电流
转化为d轴电流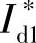 ,借助对
,借助对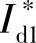 进行闭环控制来实现对实际磁链的控制。直接控制的实现较复杂,这里仅讨论间接控制方法。
进行闭环控制来实现对实际磁链的控制。直接控制的实现较复杂,这里仅讨论间接控制方法。
为将图2-21给出的磁链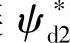 转化为d轴电流
转化为d轴电流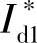 ,需建立
,需建立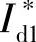 与
与 间的传递函数关系。
间的传递函数关系。
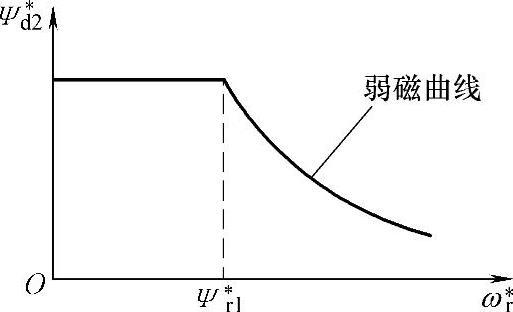
图2-21 转子磁链随转速变化曲线
首先,从d-q轴转子磁链方程:

解出:

然后,将式(2-29)代入d-q坐标系下异步电动机电压平衡方程组(2-16),得:
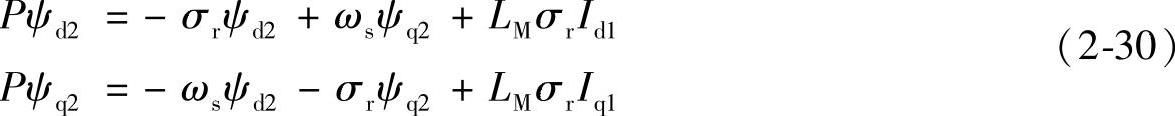
式中,σr=R2/L2。
考虑到此处讨论间接控制,上式中各变量为指令值应加上*号上标,重写该式
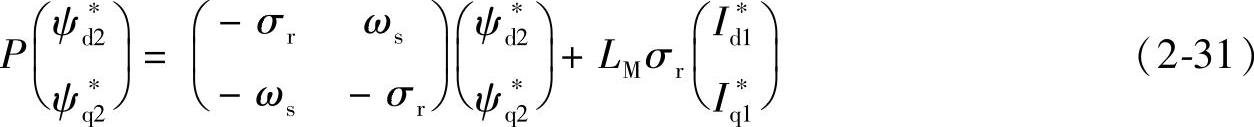
因磁场定向后,转子磁链ψ2的方向与d轴方向一致,有 ,
, ,于是式(2-31)第一行可简化为
,于是式(2-31)第一行可简化为

最后,对式(2-32)进行拉氏变换,即可得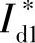 与
与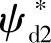 间的传递函数
间的传递函数

式中,s为复变量。在给定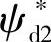 的情况下,按照式(2-33)即可求出对应的电流
的情况下,按照式(2-33)即可求出对应的电流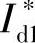 ,然后对其进行闭环控制,即可实现异步电动机的弱磁调速。
,然后对其进行闭环控制,即可实现异步电动机的弱磁调速。
根据上述原理构成的具有弱磁控制功能的异步电动机矢量变换调速系统的基本结构如图2-22所示。
现代数控机床越来越多要求主轴驱动系统具有位置闭环控制功能。对于异步伺服主轴的位置控制系统,只需在上述速度控制系统的基础上,加上转角位置闭环即可。系统结构如图2-23所示。该系统可以工作于位置闭环和速度闭环两种模式。当工作于位置闭环模式时,电动机速度控制系统的速度指令取自位置控制器。当工作于速度闭环模式时,速度指令直接由数控装置给出,位置环处于旁路。
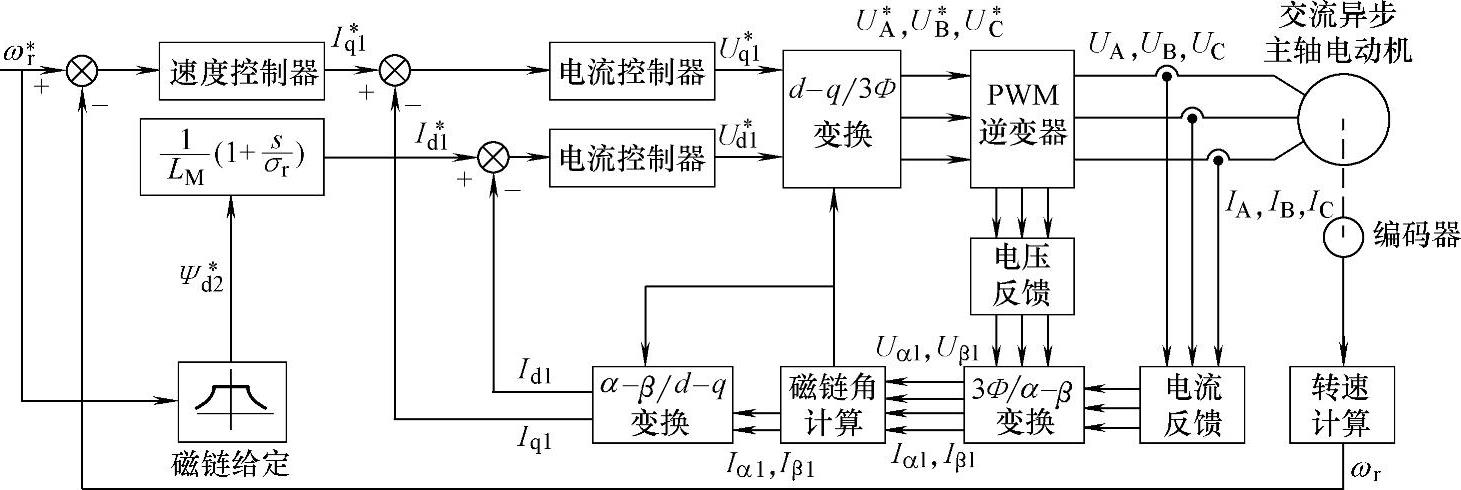
图2-22 具有弱磁控制功能的异步电动机矢量变换调速系统
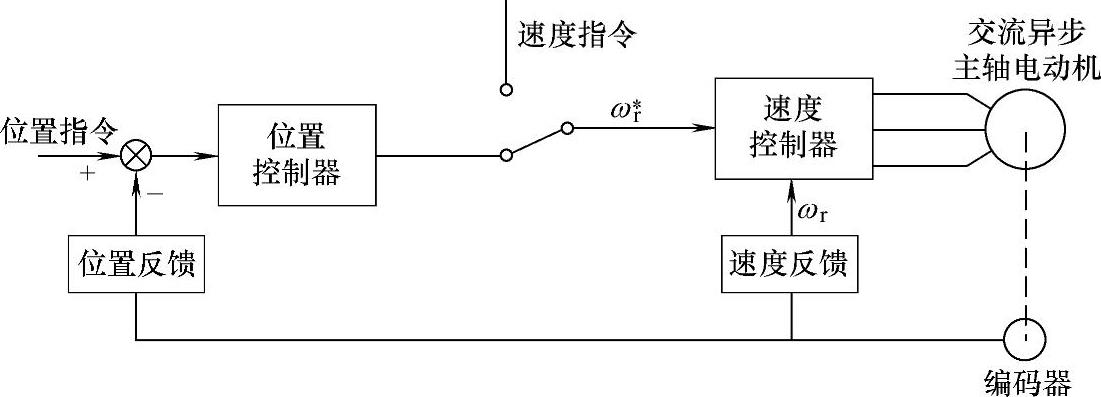
图2-23 异步伺服主轴位置控制系统
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




