数据采样插补法优化技巧

在使用基准脉冲插补法的数控系统中，插补的结果是输出进给脉冲，伺服系统根据进给脉冲进给。每进给一步（一个脉冲当量），都要进行一次插补，进给速度受插补速度的限制，很难满足现代数控机床高速度的要求。在使用数据采样插补法的系统中，数据采样插补用小段直线来逼近给定轨迹，插补输出的是下一个插补周期内各坐标轴要运动的距离，不需要每走一步脉冲当量插补一次，从而可达到很高的进给速度。

图1-20 DDA圆弧插补轨迹

数据采样插补根据用户程序的进给速度，将给定轮廓曲线分割为每一插补周期的进给段，即轮廓步长。每一个插补周期，执行一次插补运算，计算出下一个插补点（动点）坐标，从而计算出下一个周期各个坐标的进给量，如：ΔX、ΔY等，从而得出下一插补点的指令位置。与基准脉冲插补法不同，由数据采样插补算法得出的不是进给脉冲，而是用二进制表示的进给量，也就是在下一插补周期中，轮廓曲线上的进给段在各坐标轴上的分矢量。计算机定时对坐标的实际位置进行采样，采样数据与指令位置进行比较，得出位置误差，再根据位置误差对伺服系统进行控制，达到消除误差、使实际位置跟随指令位置的目的。插补周期可以等于采样周期，也可以是采样周期的整倍数。对于直线插补，动点在一个插补周期内运动的直线段与给定直线重合；对于圆弧插补，动点在一个插补周期内运动的直线段以弦线或切线、割线逼近圆弧。

图1-21 弦线逼近法

圆弧插补常用弦线逼近的方法，如图1-21所示。用弦线逼近圆弧，会产生逼近误差E_r。设δ为一个插补周期逼近弦所对应的圆心角，r为圆弧半径，则

将式（1-18）用幂级数展开，得

设T为插补周期，F为进给速度，则进给步长L为

L=TF（1-20）

用进给步长代替弦长，有

δ=L/F=TF/r（1-21）

将上式代入式（1-19），得

从式（1-22）可以看出，逼近误差与速度、插补周期的平方成正比，与圆弧半径成反比。在一台数控机床上，允许的插补误差是一定的，它应小于数控机床的分辨率，即应小于一个脉冲当量。那么，较小的插补周期，可以在小半径圆弧插补时允许较大的进给速度。从另一角度讲，在进给速度、圆弧半径一定的条件下，插补周期越短，逼近误差就越小。但插补周期的选择要受计算机运算速度的限制。首先，插补计算比较复杂，需要较长时间。此外，计算机除执行插补计算之外，还必须实时地完成其他工作，如：显示、监控、位置采样及控制等。所以，插补周期应大于插补运算时间与完成其他实时任务所需时间之和。插补周期一般是固定的。插补周期确定之后，一定的圆弧半径，应有与之对应的最大进给速度限定，以保证逼近误差不超过允许值。数据采样插补的具体算法有多种，如：时间分割法、扩展DDA法、双DDA法等。

1.时间分割法插补原理

（1）时间分割法直线插补原理

时间分割插补法是典型的数据采样插补方法。它首先根据加工指令中的进给速度F，计算出每一插补周期的轮廓步长L，即用插补周期为时间单位，将整个加工过程分割成许多个单位时间内的进给过程。插补计算的主要任务是计算出下一个插补点的坐标，即下一个插补周期内的各个坐标的进给量ΔX、ΔY控制X、Y坐标协调进给，走出逼近直线段，到达下一个插补点。在进给过程中，对实际位置进行采样，与插补计算的坐标值进行比较，得出位置误差，位置误差在后一个采样周期内修正。采样周期可以等于插补周期，也可以小于插补周期，如：插补周期的1/2。

设指令进给速度为F，其单位为mm/min，插补周期8ms，轮廓步长L的单位为μm，则

无论进行直线插补还是圆弧插补，都必须先用式（1-23）计算出单位时间（插补周期）的进给量，然后才能进行插补点的计算。

设要加工XY平面上的OA，如图1-22所示，直线起点在坐标原点O，终点为A（X_e，Y_e）。当刀具从O移动到A点时，X轴和Y轴移动的增量分别为X_e和Y_e。要使动点从O到A沿给定直线运动，必须使X轴和Y轴的运动速度始终保持一定比例关系，这个比例关系由终点坐标X_e，Y_e的比值决定。

图1-22 时间分割法直线插补

设要加工的直线与X轴的夹角为α，轮廓步长为L，即单位时间间隔（插补周期）的进给量。于是有：

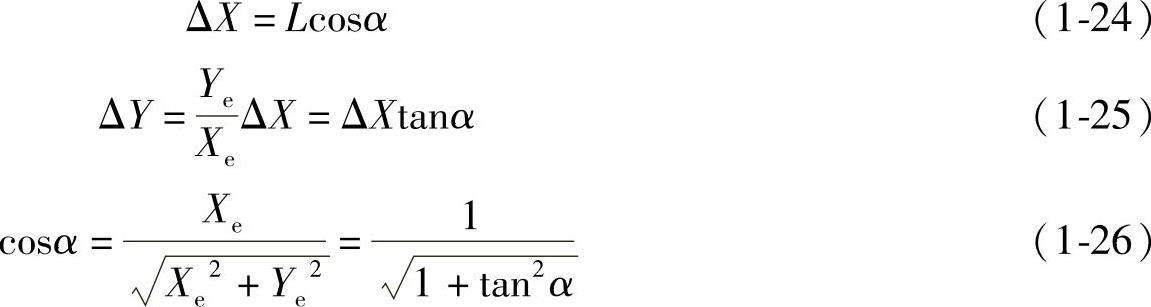
式中，ΔX为X轴插补进给量；ΔY为Y轴插补进给量。

时间分割插补法插补计算结果，就是算出下一单位时间间隔（插补周期）内各个坐标轴的进给量。因此，时间分割插补法插补计算可按以下步骤进行。

①根据加工指令中的速度值F，计算轮廓步长L。

②根据终点坐标值X_e、Y_e，计算tanα。

③根据cosα，计算tanα。

④计算X轴进给量ΔX。

⑤计算Y轴进给量ΔY。

在进给速度不变的情况下，各个插补周期ΔX，ΔY不变，但在加减速过程中是要变化的。为了和加减速过程采用统一的处理办法，所以即使在匀速段也进行插补计算。

（2）时间分割法圆弧插补原理

时间分割法圆弧插补，也必须根据加工指令中的进给速度F，计算出轮廓步长，即单位时间（插补周期）内的进给量L，才能进行插补运算。圆弧插补运算，就是以轮廓步长为圆弧上相邻两个插补点之间弦长，由前一个插补点的坐标和圆弧半径，计算由前一插补点到后一插补点两个坐标轴的进给量ΔX、ΔY。

如图1-23所示的顺圆弧，A点为圆弧上的一个插补点，其坐标为（X_i，Y_i），B点为经A点之后一个插补周期应到达的另一插补点，B点也应在圆弧上。A点和B点之间的弦长等于轮廓步长L。AP是圆弧在A点的切线，M是弦AB的中点，OM⊥AB，ME⊥AF，E为AF的中心。圆心角具有以下关系：

ϕ_i+1=ϕ_i+δ （1-27）

式中，δ是轮廓步长L所对应的圆心角增量，也称步距角。

图1-23 时间分割法圆弧插补

因为OA⊥AP，所以△AOC～△PAF，则

∠AOC=∠PAF=ϕ_i （1-28）

由于AP为切线，所以有

在△MOD中

将DH=X_i，OC=Y_i，和，代入式(1-31)．则有(www.xing528.com)

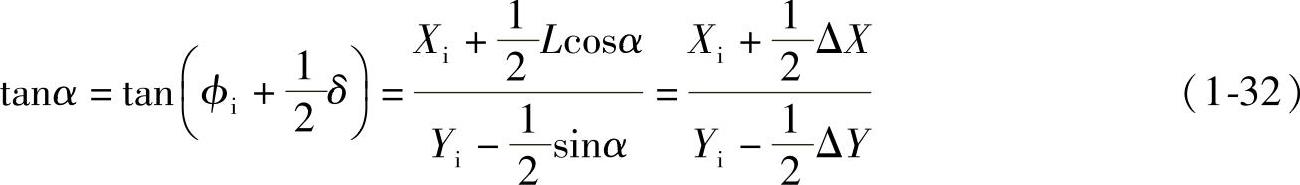
式中，cosα和sinα均为未知，要计算tanα仍很困难。为此，采用一种近似算法，即以cos45°和sin45°来代替cosα和sinα。这样，式（1-32）可改写为

因为A点坐标X_i、Y_i为已知，要求B点坐标可先求X轴的进给量。

由于A和B是圆弧上相邻两点，必然满足下列关系式：

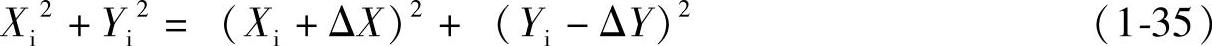
将式（1-30）展开整理后可得

由此可以得到下一个插补点B的坐标值：

在用式（1-33）进行近似计算tanα势必造成tanα的偏差，进而造成ΔX的偏差。但是，这样的近似计算并不影响B点仍在圆弧上。这是因为ΔY是通过式（1-36）计算出来的，满足式（1-36），B点就必然在圆弧上。tanα的近似计算，只造成进给速度的微小偏差，实际进给速度的变化小于指令进给速度的1%。这么小的进给速度变化在实际切削加工中是微不足道的，可以认为插补速度是均匀的。

时间分割插补法用弦线逼近圆弧，因此，插补误差主要为半径的绝对误差。插补周期是固定的，该误差取决于进给速度和圆弧半径，见式（1-22）。为此，当加工的圆弧半径确定后，为了使径向误差不超过允许值，对进给速度有一个限制。

由式（1-22）可得

式中，E_r是最大径向误差；r是圆弧半径。

当要求E_r≤1μm，插补周期T=8ms时，进给速度

2.扩展DDA数据采样插补法

和前面介绍的数字积分插补法相似，扩展DDA算法是在数字积分原理的基础上发展起来的。它在处理圆弧插补时，不是直接应用数字积分，而是对数字积分法做了改进，将数字积分法用切线逼近圆弧的方法改进为割线逼近，减小了逼近误差。

图1-24 扩展DDA直线插补

（1）扩展DDA直线插补原理

设要加工的直线为OP，其起点为坐标原点O，终点为P（X_e，Y_e），要在时间T内走完OP直线，如图1-24所示。V为进给速度（mm/min），V_x与V_y分别为X、Y坐标的分速度。则有：

由数字积分原理可得：

将时间T用采样周期Δt分割成n个子区间（n取大于等于最接近的整数），则可得到下式：

由此可导出直线插补的迭代公式：

轮廓步长在坐标轴上的分量ΔX、ΔY的大小取决于编程的进给速度V，其表达式为：

（2）扩展DDA圆弧插补原理

设要加工第一象限顺圆，其圆心在原点O，半径为R，若刀具处在插补点位A（X_m，Y_m）的位置，如图1-25所示。

图1-25 扩展DDA圆弧插补

根据数字积分已导出的公式：

从而有：

设轮廓步长为L，如果直接用数字积分计算，则有：

按上式计算，进给方向为合成速度V的方向。从图1-25可以看出，在插补点A（X_m，Y_m）时V的方向是该点的切线方向。以切线逼近圆弧，势必造成较大的逼近误差。扩展DDA插补法将DDA的切线逼近改进为割线逼近，从而提高插补精度。如图1-25所示，用DDA的算法求出按切线方向的各坐标轴增量ΔX、ΔY，取其可得到点B（X_n，Y_n）的坐标：

再以直线OB的垂线BC方向作为合成速度方向计算实际进给的增量ΔX′和ΔY′。

在图1-25中，从A点按BC的方向进给，走出割线AD，因而本次插补周期应到达的坐标位置为D（X_m+1，Y_m+1）。