数字积分法：快速、均匀的插补算法

数字积分法又称数字微分分析法DDA（Digital Differential Analyzer），是在数字积分器的基础上建立起来的一种插补算法。最初在硬件数控系统中是使用逻辑电路实现积分运算，现在可由软件实现。数字积分法具有运算速度快、脉冲分配均匀、易实现多坐标联动、较容易实现二次曲线、高次曲线插补等优点。

1.DDA直线插补

（1）DDA直线插补原理

设在平面中有一直线OA，其起点为坐标原点O，终点为A（X_e，Y_e），动点移动速度为V，则动点在X和Y方向的分速度为：

式（1-8）中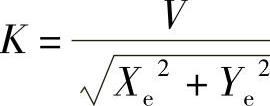，，K为常数。

对式（1-8）进行积分即可得到X轴和Y轴在时间周期t的移动距离：

上式积分用累加的形式近似为：

动点从原点出发走向终点的过程，可以看做是各坐标轴每隔一个单位时间Δt，分别以增量KX_e及KY_e同时对两个累加器累加的过程。当累加值超过一个坐标单位（脉冲当量）时，产生溢出，溢出脉冲驱动伺服进给一个脉冲当量，从而走出给定直线。

若经过m次累加后，X和Y分别到达终点（X_e，Y_e），即下式成立：

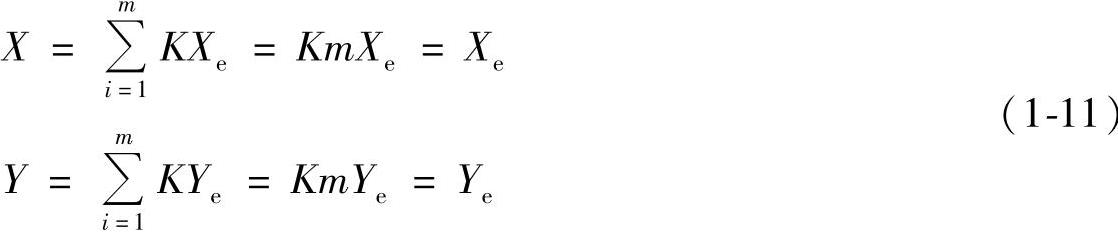
由此可见，比例系数K和累加次数之间有如下的关系：

Km=1，即m=1/K

K的数值与累加器的容量有关。累加器的容量应大于各坐标轴的最大坐标值，一般两者的位数相同，以保证每次累加最多只溢出一个脉冲。设累加器有n位，则

K=1/2 ⁿ （1-12）

故累加次数为

m=1/K=2 ⁿ （1-13）

上述关系表明，若累加器的位数为n，则整个插补过程要进行2 ⁿ次累加才能到达直线的终点。

因为K=1/2 ⁿ，n为寄存器的位数，对于存放于寄存器中的二进制数来说，KX_e（或KY_e）与X_e（或Y_e）是相同的，可以看做前者小数点在最高位之前，而后者的小数点在最低位之后。所以，可以用X_e直接对X轴累加器累加，用Y_e直接对Y轴的累加器累加。

图1-17为DDA平面直线的插补运算框图。它由两个数字积分器组成，每个坐标轴的积分器由累加器和被积函数寄存器组成。被积函数寄存器存放终点坐标值。每隔一个时间间隔Δt，将被积函数的值向各自的累加器中累加。X轴的累加器溢出的脉冲驱动X轴走步，Y轴累加器溢出脉冲驱动Y轴走步。

对于不同象限的处理方法与逐点比较法相同。仍然是把符号与数据分开，取数据的绝对值作被积函数，而以符号作进给方向控制信号处理，便可对所有不同象限的直线进行插补。

（2）直线插补计算过程

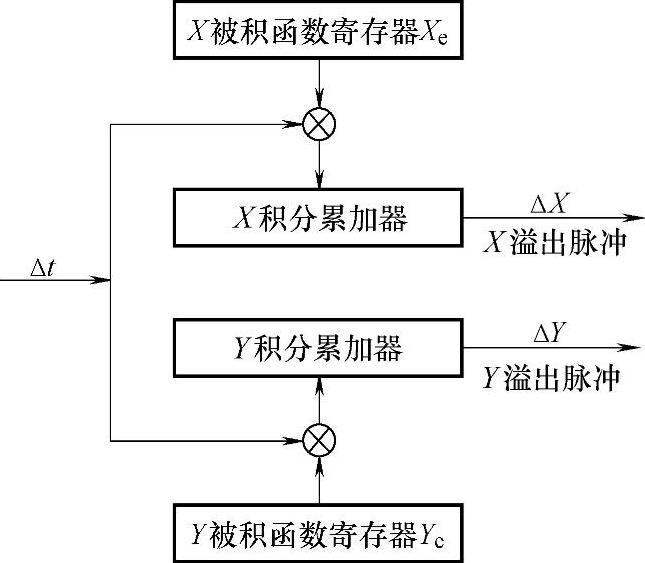
图1-17 DDA平面直线的插补运算框图

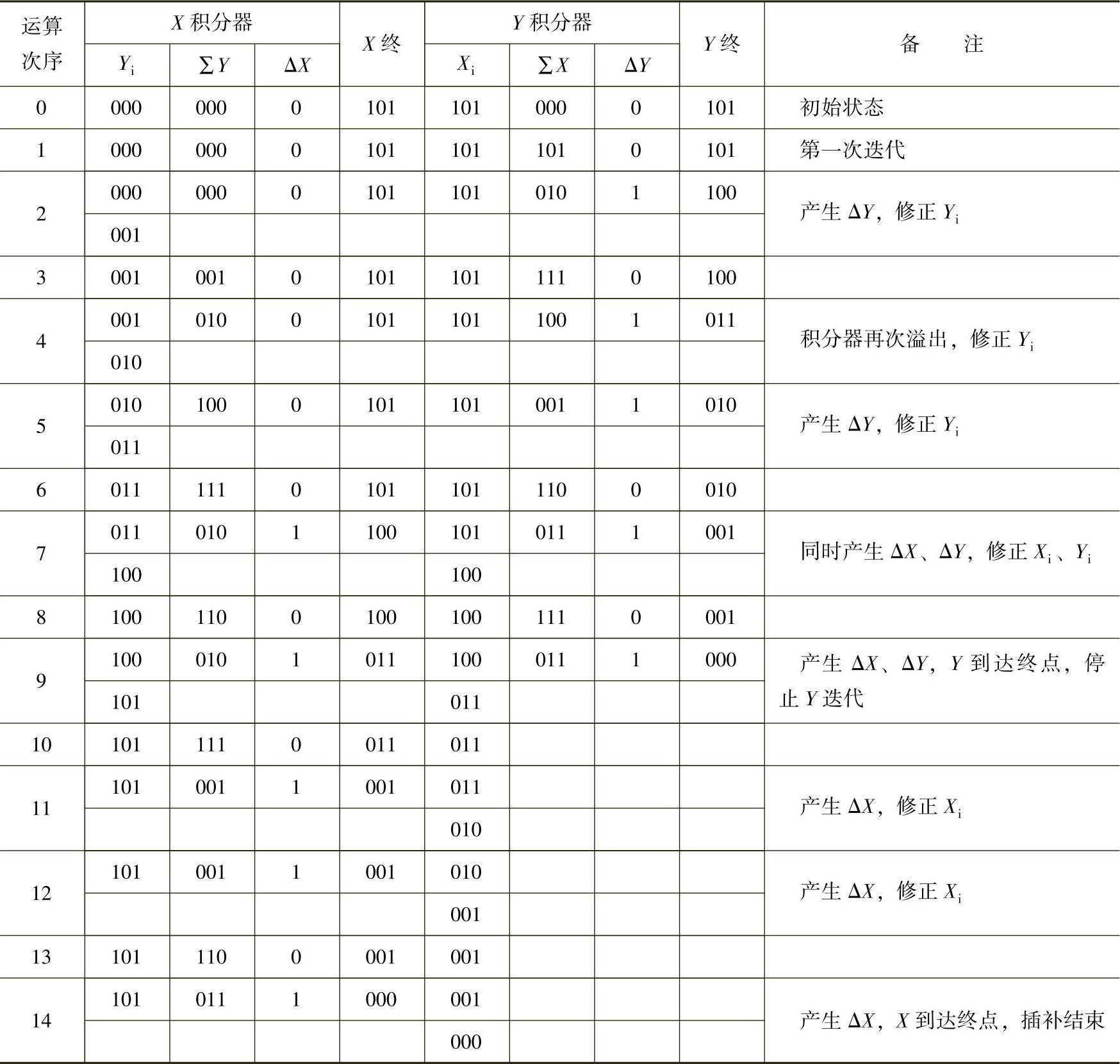
在图1-18中，设有一直线OA，起点为原点O，终点A坐标为（5，3），累加器和寄存器的位数为3位，其最大容量为2³=8。采用数字积分法进行直线插补计算过程如表1-5所示。插补轨迹如图1-18所示。

表1-5 DDA直线插补计算过程(www.xing528.com)

2.DDA圆弧插补

（1）圆弧插补原理

DDA直线插补的物理意义是使动点沿速度矢量的方向前进。这同样适用于DDA圆弧插补。

如图1-19所示，圆的方程为

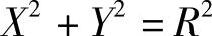
式中R是常数，X、Y是以时间t为参数的变量。等式两边同时对t求导数，则有

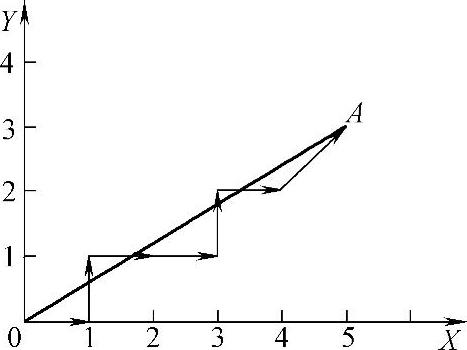
图1-18 DDA直线插补轨迹

对式（1-14）进行变换有

图1-19 XY平面DDA圆弧插补

由此导出第一象限逆圆弧加工时动点沿坐标轴方向的速度分量为：

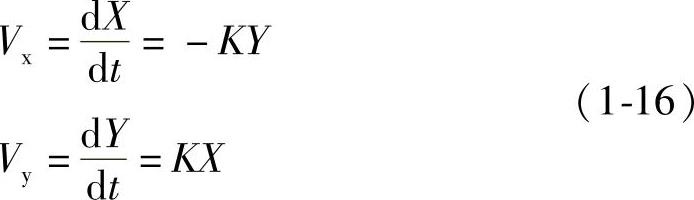
式（1-16）中，K为常数，因此第一象限逆圆弧加工时DDA插补表达式为：

式（1-17）表明：X轴的被积函数值等于动点Y坐标的瞬时值，Y轴的被积函数值等于动点X坐标的瞬时值。与直线插补比较可知：直线插补时，为常数累加；圆弧插补时，为变量累加。

对于累加过程来讲，累加进位的速度和连减借位的速度是相同的，所以，X轴被积函数的负号可忽略，两个轴的插补都用累加来进行。

数字积分圆弧插补时，两轴不一定同时到达终点，可以采用两个判终计数器（判断是否到达终点的计数器），各轴分别判终，进给一步减1，判终计数器减为0时，该轴停止进给。两轴都到达终点后停止插补。

与逐点比较法类似，将进给方向单独处理，而用动点坐标的绝对值进行累加。

（2）DDA圆弧插补过程

假设加工第一象限逆圆弧，其圆心在原点，起点A坐标为（5，0），终点B坐标为（0，5），累加器为3位，采用数字积分法进行插补脉冲计算，如表1-6所示，插补轨迹如图1-20所示。因为插补过程中要对刀具位置坐标数值进行累加，因此，一旦累加器发生溢出，即说明刀具在相应坐标方向走了一步，则必须对其坐标值，即被积函数进行修改。在图1-20中，两坐标进给步数均为5。在插补中，一旦某坐标进给步数达到了要求，则停止该坐标方向的插补运算。

表1-6 DDA圆弧插补过程