变流器输入功率的相关分析

如上所述，变流器的输入电流是非正弦的，并且可以表示为高次谐波电流和的形式。此时基波电流的有功分量与网络电压相位一致，而无功分量滞后于电压90°。此时，需要对变流器中的潮流进行专门分析。

下面分析单桥式变流器的潮流，为了简化，认为阀换向角γ=0，хк=0。此时，假设变流变电站母线上的电压是正弦的和对称的，而桥的相电流是矩形波形式，同样认为变压器的两个绕组连接成星型。此时网络绕组电流与阀绕组电流波形相同，并且形成了两个不同极性的矩形分段，每个分段长度为120°。

在此使用瞬时功率的概念。正的瞬时功率说明电能由电网流入变流器，负的瞬时功率说明电能由变流器流入电网。

在变流器输入端，相瞬时功率被确定为：

p=ei=e （i₁+Σi_n） （12.27）

其中 e和i——相电流和电压的瞬时值；

i₁——基波的瞬时值；

∑i_n——高次谐波电流瞬时值之和。

对于所采取的相应于相电动势еА和еВ交点的坐标原点，网络电压和基波电流的表达式为：

e=E_msin （ϑ-30°） （12.28）

i₁=I_m1 sin （ϑ-30°-α）

功率的平均值，决定了变流器在一个周期内所需要的能量，且等于功率的有功分量

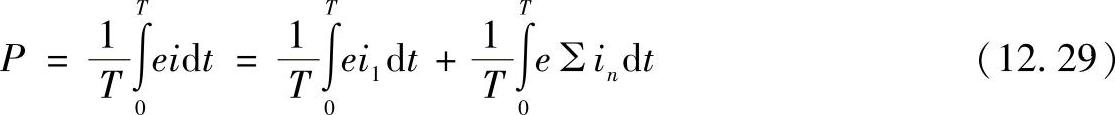
已知的是，上述表达式第二项中积分号下的是各种频率正弦波乘积之和，等于0。由此可以得出，在所采取的假设下，有功功率只是基波电流与电压的积分，其值可以将（12.28）中的电流和电压代入后通过（12.29）式得到。积分后单相有功功率为

应该说明，此时（γ=0）电压和基波之间的相位角只是由角度α决定，因此φ₁=α。

变流器输入端三相功率平均值之和

考虑到

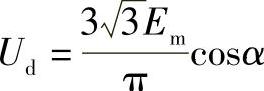
得到

P=U_dI_d

换句话说，整个三相有功功率被传到了直流回路，变流器三相功率的时间曲线如图12.15所示。

平滑电抗器前变流器直流侧三相瞬时功率含有直流和交流分量，在电抗器之后只是剩下了直流分量，因为极电流和电压随时间变化。瞬时功率的交流分量被电抗器吸收，此时其符号发生变化。由此可以看出，电抗器与交流网络之间进行功率交换。

三相变流器输入端的全功率可以表示为(www.xing528.com)

S=3EI

其中 I，E——变流器相电流和网络全电压的有效值。

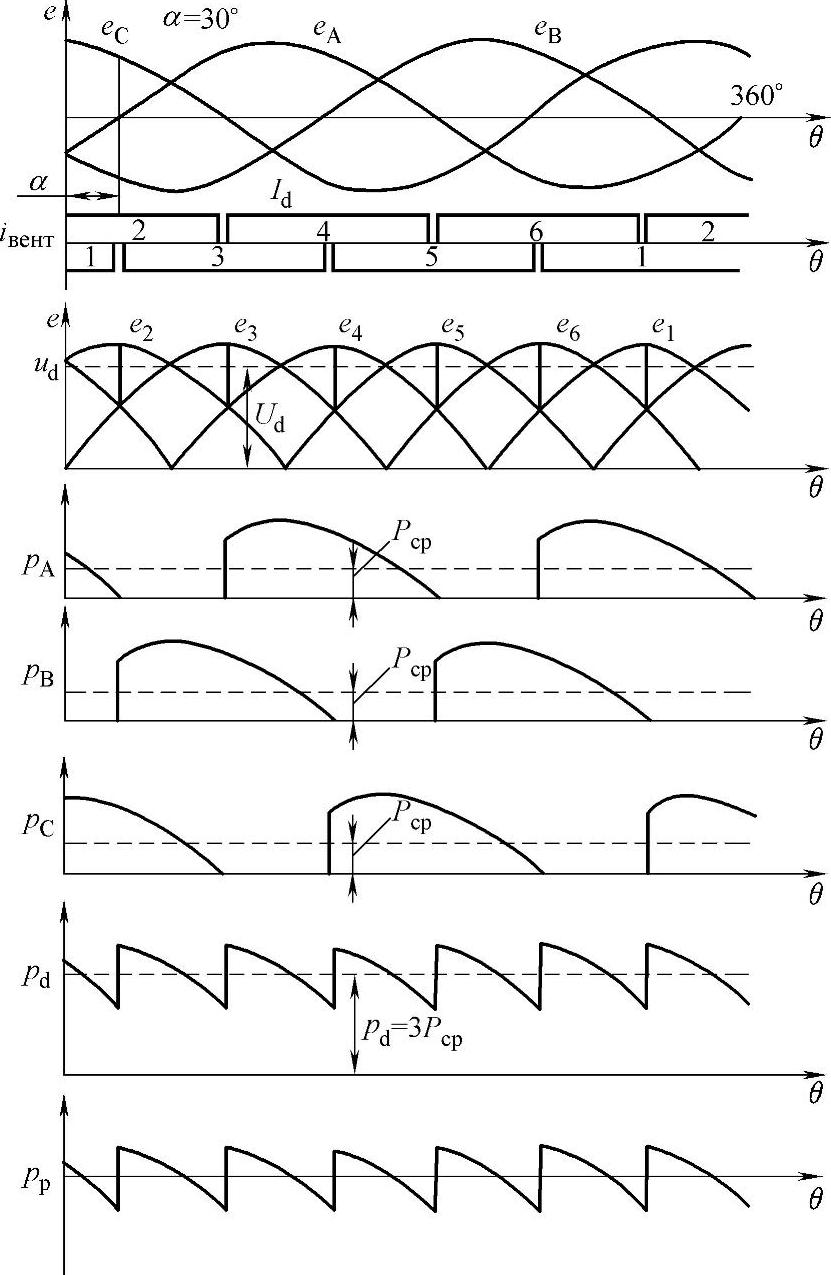
图12.15 变流器三相功率的时间曲线

考虑到相全电流是各个谐波电流之和，可以得到

计及

I²₁=I²_1a+I²_1r

将其前面的因子引入到根号下，有：

变流器输入端全功率有三个分量：

Р——有功功率；

Q₁——被基波电流无功分量决定的无功功率；

Т——与高次谐波电流流通有关的畸变功率。

功率的有功分量被如上所示的（12.31）确定。对于整流器，无功分量可以按照基波得到

畸变功率由下面的表达式确定

整个变流器的功率因数等于

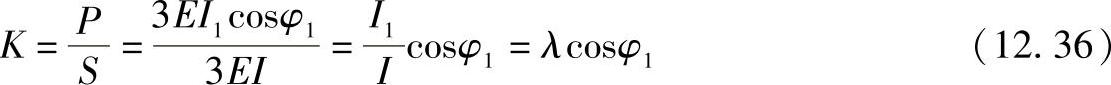
其中 λ——畸变系数，λ=I₁/I，由阀的换向角决定

在此，当γ=0时畸变系数等于λ=0.955，并且随着换向角的增大而增大。