实际变流器中的谐波电流优化方案

计及控制角和换向角时的实际变流器电流如图12.4所示。

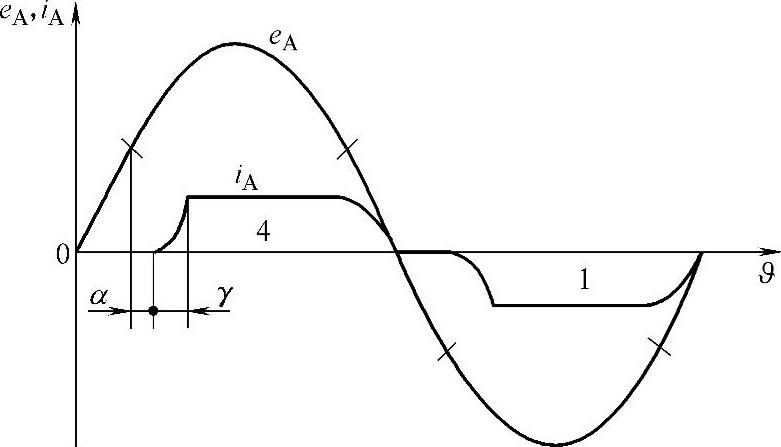
图12.4 当变压器接线为Yy时的实际变流器 电流：1，4—相应的阀电流

可以进行类似的谐波分析，而无需给出完全分解情况下的傅里叶级数。

当α＞0时，基波电流有：

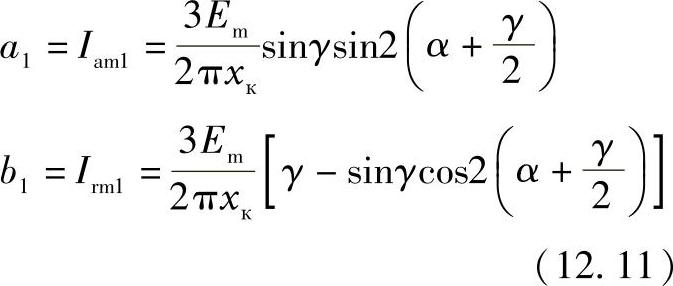
其中 I_am1，I_rm1——基波电流的有功和无功分量幅值。

考虑到

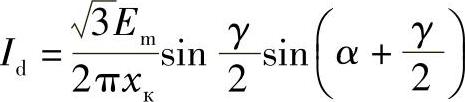
同时假设

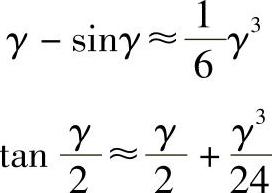
经过一些变换后得到

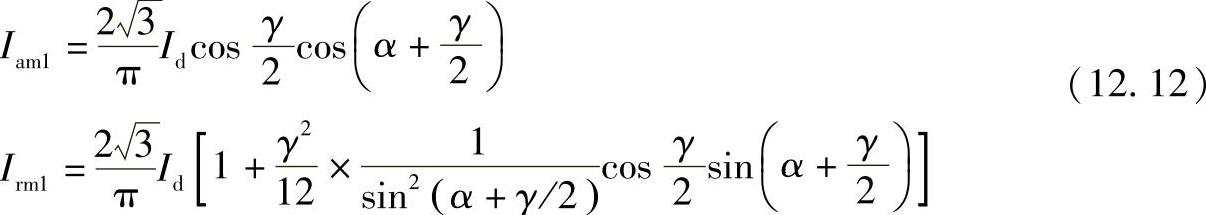
对于实际的工程计算来说，上述表达式的精确度是足够的，基波电流的幅值可以按照下式得到

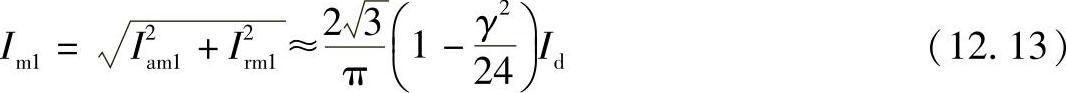
当γ＜30°时，表达式（12.13）可以简化，误差小于1%时可以采取

由此，基波的有效值为

整流器和逆变器全电流及其有功部分之间的相角差，可以按照下式得到（此相角差决定了变流器的功率因数）

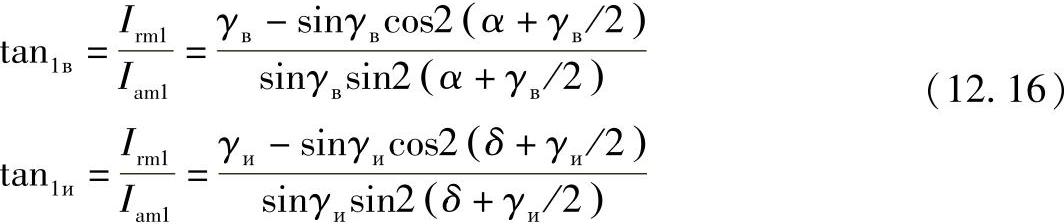
为了简化计算，当计及αи=180-β时，可以使用从式（12.16）得到的表达式

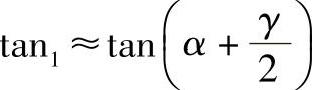
或者

但是应该注意，当α和γ的实际可能值较小时，这些表达式有明显的误差。因此在精确计算时应当使用方程（12.16）。(www.xing528.com)

当n=5，7，11，13…时的高次谐波有：

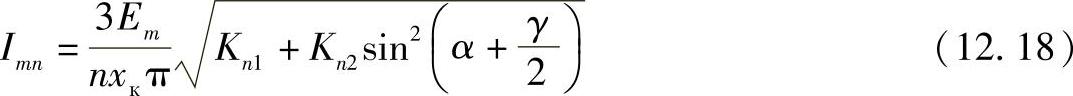
其中

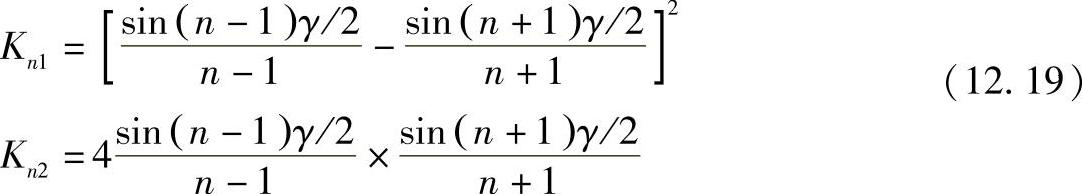
计及换向角时，变流器的电流波形不是矩形波，而是稍微接近于正弦波。因此谐波幅值减小，尽管其次数还是由式（12.4）决定，这种情况如图12.5所示。从中可以看出，高次谐波的含量随着电流的增加而减小，这可以解释为换向角增加了。

在图12.6列出了5次和7次谐波电流与角度γ的关系，当γ=0时代表阶梯状的矩形波，这些谐波有最大值。那么按照简化的方程（12.6）和（12.7）计算，与考虑实际的电流波形计算相比，非正弦含量增加了。

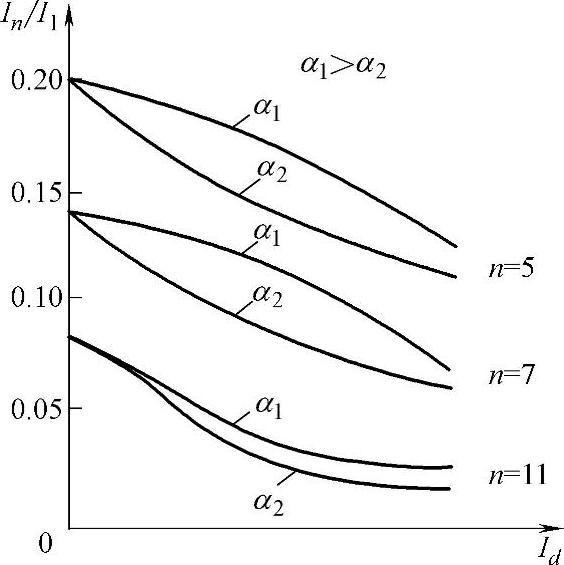
图12.5 高次谐波电流与负载电流的关系

变流器电流中高次谐波的含量以非正弦系数表示

其值并没有被规定。

直流输电线路变流器的工作带来的不只是其从电网中吸收的电流波形畸变，还有电压波形的畸变问题。变流器是高次谐波电流源，高次谐波在网络中传播，从而引起感抗上的电压降落，结果使得网络节点及用户母线上的电压畸变。最严重的畸变发生在变流器母线上（见图12.7），这些畸变是由变流器和系统容量比决定的。当变流器的功率较小时，其母线上的电压畸变是最小的，随着变流器功率的增加畸变也越来越严重。对于直流输电线路，当其功率与送端和受端系统的功率差不多时，电压畸变是非常严重的，因此在变流站上一定要采取高次谐波补偿措施。

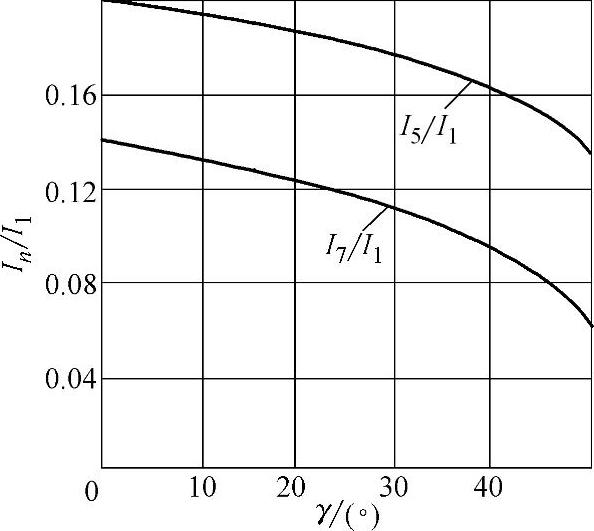
图12.65 次和7次谐波电流与换向角的关系

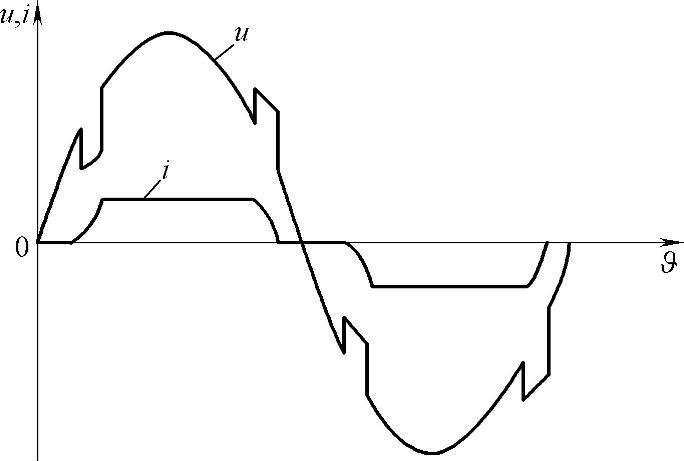
图12.7 变流器母线上的电压畸变

下面从交流系统侧分析变流站母线上的电压畸变。变流器的高次谐波电流在系统的等值阻抗上产生了电压损耗

U_n=I_nnxсист （12.21）

将式（12.18）中的电流值代入，可以得到

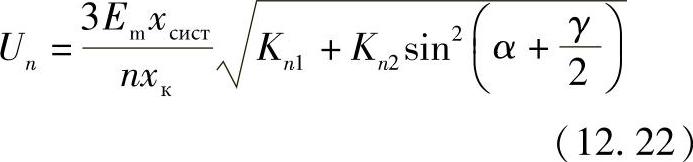
可以看出，高次谐波的电压依赖于系统的等值阻抗，换句话说，就是依赖于其功率。系统提供给变流器的功率越大，其母线上的电压畸变越小。

电压畸变由电压的非正弦系数决定

目前，只是对于110kV以下的网络规定了其数值。对于220kV及以上的网络，具有大功率的变流站，K_U的值没有统一的标准，规定其值时必须考虑每一种具体的情况。