不可控整流器和逆变器的协同工作研究：a、b常数的影响

上面已经说明，当变流站母线电压为正弦时，可以不考虑整流器和逆变器相邻桥之间的相互影响。因此，本节将进一步分析单桥变流器——整流器和逆变器的协同工作。

线路中的电流是由其两端的电压差决定的

式中 U_dв和U_dи——整流器和逆变器输出端、线性电抗器后面电压的平均值。

如上所述，U_dв和U_dи是状态参数——负载电流I_d和控制角a及b的函数，这些关系由整流器的外特性方程（10.60）和逆变器的外特性方程（11.12）、（11.13）决定。单桥式变流器在额定负载下工作在状态2—3上，因此将方程（10.60）和（11.12）代入到（11.25）中，得到

其中

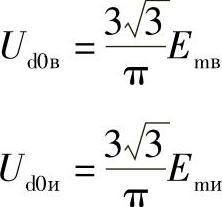
方程（11.26）在已知输电线路等值电路参数和控制角a和b时，可以用来计算线路上的电流。这个方程同样可以用来建立归算到直流侧的直流输电线路等值电路。

对应等值电路（见图11.1），整流器可以被看作电动势等于U_d0в cosα的直流发电机，其内阻抗为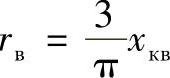；而逆变器可以被看作电动机，其产生U_d0и cosβ的反电动势，内部阻抗为。

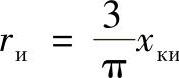在此与发电机—电动机系统一样，整流器输出端的整流电压U_d в小于整流器的电动势，而逆变器入口的整流电压U_d и大于逆变器的反电动势。

通过对角度α的作用，改变整流器的电动势，或者通过对角度β的作用，改变逆变器的反电动势，来改变线路的电流和传输功率。

用物理方法对整流器和逆变器协同工作进行分析是比较方便的。整流器和逆变器外特性的交点决定了输电线路工作状态特性。但是，为此必须计及线路上的电压损耗，从而将整流器和逆变器的特性归算到等值电路的一个点上，可以是整流器或者是逆变器的连接点。如果整流器的外特性被归算到逆变器的连接点上，其方程有如下型式：

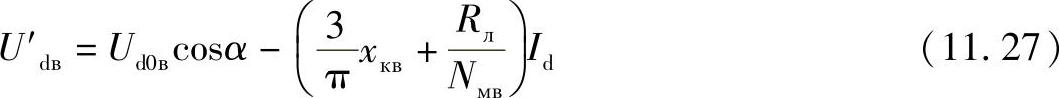
式中 N_мв——整流器桥的数量。(www.xing528.com)

下面在以物理方法分析整流器和逆变器协同工作时，将使用归算到逆变器连接点的整流器外特性。

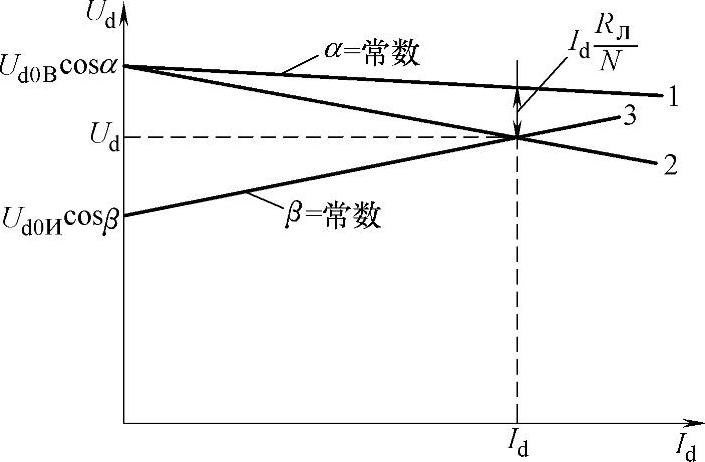
图11.15 “自然”（1）以及折算后的 （2）整流器特性；逆变器特性（3）

在图11.15上显示了整流器a=常数时的外特性（“自然”的并且归算到逆变器连接点上），以及b=常数时逆变器的外特性。

两个特性曲线的交点——被归算的整流器特性以及逆变器特性，决定了输电线路工作状态点的位置：电流I_d值和电压U_d值以及功率

P_d=U_dI_d

当角度a变化时，整流器的特性曲线平行移动，此时整流器和逆变器特性的交点以及相应的工作电流和输电线路功率（见图11.16a）也随着移动。

当整流器的电动势不变时（a=常数），通过改变角度b来改变逆变器的反电动势也可以得到类似的效果，这种情况如图11.16b所示。当控制角a和b不变时，可以用来对整流器—逆变器系统的稳定性进行简化分析。

当电流I_d突然产生距离平衡点±DI的偏差时，将产生使系统回到初始点的电动势差。当扰动为正时，反电动势大于电动势，并且电流减小；当扰动为负时，电动势大于反电动势，电流增大。即系统仍旧稳定，这种情况对任意的a和b都成立。

方程（11.26）和图11.1确定了此时几个相互独立变量之间的关系，包括角度a和b、受端和送端系统的电动势。因此，这个方程和图可以用来解决一些其他问题，例如对于给定的电流值，求解必要的整流器和逆变器控制角度值。

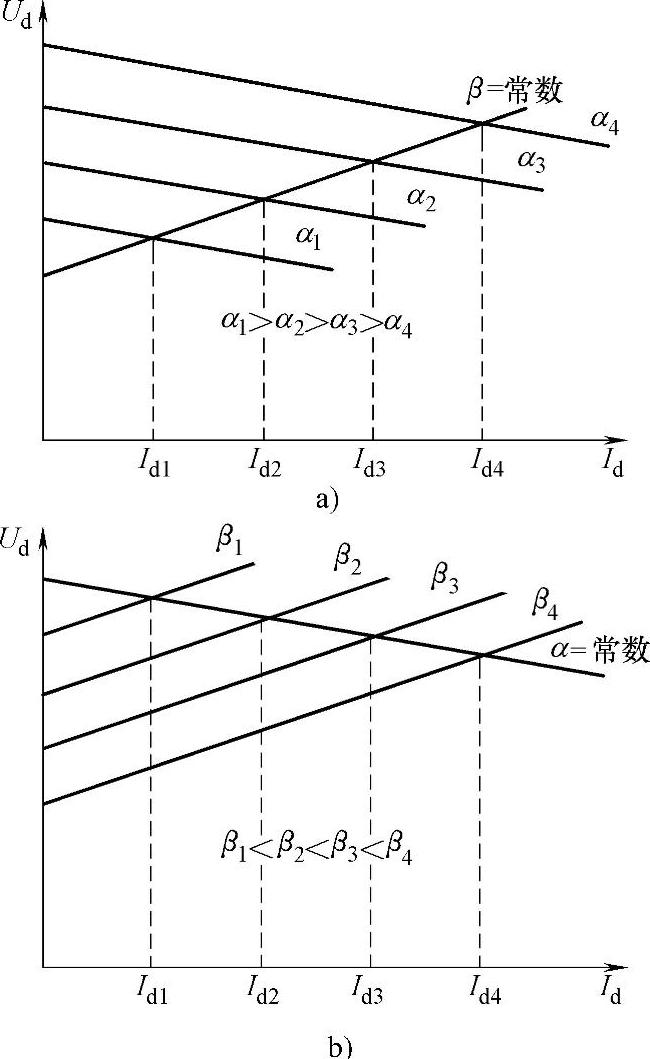
图11.16 电流I_d的控制曲线

a）角度 a变化（b=常数）； b）角度b变化（a=常数）