直流线路等值电路的计算方法

下面分析双极塔架的长直流架空线路（L＞300km）。双极塔架是指上面悬挂线路两极П₁和П₂的塔架，同样包括避雷线T。

长线路是必须要考虑其中的波过程。对于长度为dl的线路分段，其等效电路如图11.14所示。在此为了一致性，当极电流I_d1和I_d2不相等时，考虑接地电阻是合适的，此时大地中流过的电流等于极电流的差

I_з=I_d1-I_d2

图11.14 双极线路的电容示意图（a）以及线路分段的等效电路（b）

在形成等值电路时采取如下的假设：

1）导体对地电纳较小，可以忽略，因为电晕损耗比交流线路小得多；

2）避雷线是理想接地的，其导纳等于无穷大；

避雷线的对地电容等于0。

对于如图11.14所示的等效电路，存在如下关系式：

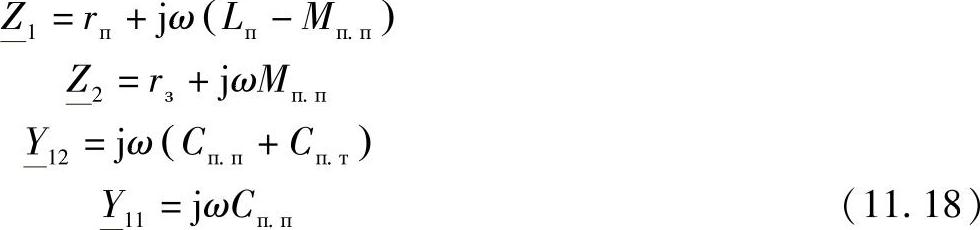
其中 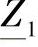——频率为w的极复阻抗；

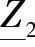——此频率下大地的复阻抗；

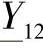——极和避雷线对地电纳；

Y₁₁——极—极之间的电纳。

L_п——极—大地之间的电感；

M_п.п——极间互感系数；

r_з——大地电阻，它是频率和单位土壤电导率的函数，采用专门的方法确定；

C_п.п——极—极之间的电容；

C_п.т——极—避雷线之间的电容。上述量给定的都是1km线路的值。

极阻抗电阻部分rп的确定需要考虑线路电极的结构，就像交流线路的相间结构一样，出于降低导体表面电场强度的目的采用分裂导线。当给定塔架和导体弧垂时，线路导体的电感、电极之间以及与大地之间的电容采用镜像法以及电动势系数法确定。

当极电流相等时I_d1=I_d2，大地中没有电流，阻抗Z₂=0，等效电路可以被简化。此时：

当线路的长度小于300km时，可以不考虑线路当中的波过程，线路可以表示为集中恒定阻抗和导纳的形式，以单位长度参数与线路长度乘积来表示：

(www.xing528.com)

如果对于长度超过300km的直流架空线路，其等值电路或者二端口网络参数应该考虑线路本身参数的分布特性，如第4章所示的方法。

应该说明，为了研究直流输电线路中的暂态过程，采取线路的Т型等值电路更加方便。如上所述的直流线路等值电路，在直流输电线路的物理和数学模型基础上，可以被用来研究直流输电的暂态和事故后过程。

同时，在稳态时（w=0），直流输电线路的状态参数变化是非常慢的，其导数可以被忽略。因此，线路的等值电路可以被简化，只以极阻抗的形式表示

R_п=r₀l （11.21）

因为在此不分析直流输电线路的暂态和事故后过程（短路，线路的带电投切等），在计算过程中线路只是被表示为电阻。

对于直流电缆线路，同样具有电感和电容，尽管这些参数之间的关系与架空线路完全不同。同样应该考虑到，电缆线路的长度一般较小，不会超过200km，在暂态过程中不一定要计及波过程。因此，在稳态时电缆线路同样被表示成电阻的形式。

考虑到双极输电线路两侧每极上安装的线性电抗器，以及两个半回路负载相同（I_d1=I_d2），线路的全阻抗等于

R_л=2（2R_р+R_п） （11.22）

对于单极输电线路，具有经过大地的返回电流，线路的电阻为

R_л=2R_р+R_п+R_з （11.23）

其中 R_з——大地的全电阻；

R_р——线性电抗器的电阻。

大地的全电阻由两部分构成：接地分流电阻和大地的自电阻。

分流电阻由接地装置的结构决定，通常是很小的，例如对于伏尔加格勒—顿巴斯的直流输电线路只有零点几欧姆。至于大地本身的电阻，就像已经说明的那样，直流流经整个大地，在距离接地装置几百米的地方电流密度可以忽略（当管线附近没有电缆和其他的工程设施时），因此大地的自电阻可以认为等于0。

直流回路中线性平滑电抗器的阻抗由其结构决定，并且可以根据厂家的数据得到。在没有电抗器阻抗的情况下，可以在下面表达式基础上进行近似得到。

平滑电抗器功率损耗的相对值是

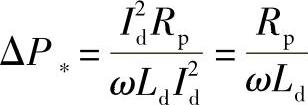
其中 R_р——电抗器的电阻；

w——f=50Hz时的角频率；

w=314L_d——电抗器的电感。

由此

R_р=ωL_d ΔP_∗ （11.24）

对于维堡直流站的电抗器（I_ном=2.1kA，L_d=0.102H，ΔP=178kW），ΔP∗=0.0013（或者0.13%）。大功率直流输电线路电抗器中的相对损耗也差不多是这个值。应该注意到，对500kV交流并联电抗器ΔP_∗=0.3%，即这些量在同一个数量级上。但是，在直流线路上由于没有电流的滞后和超前现象，其损耗要相对小一些。

在一定的范围内给定ΔP_∗的值，以及电抗器的电感（在0.5～1.5H范围内），可以确定电抗器的阻抗。计算表明，线路电极的总阻抗总体来说是由线路导体的电阻决定的。例如，对于长度为2400km的直流输电线路，极阻抗可以达到18Ω，而通常在输电线路的首端和末端连接到电极上电抗器的阻抗，大概是0.9Ω。