单桥式逆变器的工作状态解析

逆变器的任务是将由整流器提供的直流电能变换为交流电能，并且将此电能传输给受端系统。逆变器是借助于具有可逆特性的桥式变流器实现的，可以通过增加阀控制角a使其过渡到逆变状态。过渡条件由式（10.69）确定。

由图10.27和10.28可以看出，当＞90°时，整流电压的极性发生变化，即变流器产生与角度a有关的反向电动势。当a在从90°到接近180°的范围内增大时，反向电动势增加。通过改变控制角度可以改变逆变器反向电动势的值，从而可以改变整个输电线路或者直流换流站的状态。

在直流回路建立电动势的整流器，以及具有反向电动势的逆变器的协同工作可以类比通过线路连接起来的发电机和电动机的协同工作——发电机产生电动势，而电动机产生反向电动势。

直流回路的电流无论在什么情况下都取决于电源电动势和电能接受端反向电动势的差，以及直流回路的总阻抗，包括线路阻抗、电源和电能接受端的自阻抗：

直流侧直流输电线路的等值电路如图11.1所示。

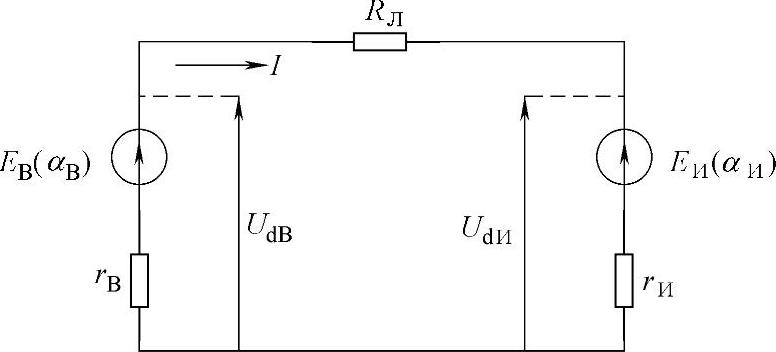
图11.1 直流侧直流输电线路的等值电路

式（11.1）的左侧和右侧同时乘以Е_в（a_в），得到

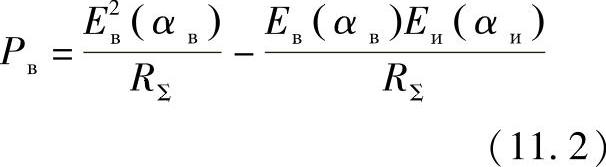
方程式（11.2）右侧第一项具有功率的特征，在本回路中作为内部损耗消耗掉了。第二项也是功率，是从这个回路输出的功率。电源的能量（除了导体发热之外）被消耗在了克服受端的反电动势上，然后变成了逆变器输出到接受端系统的电能（或电动机的机械能）。

另外，逆变器（电动机）回路的电流在直流电压的作用下从整流器侧（发电机）流过。交流受端系统的电压在逆变器中只是建立了反向电动势。除此之外，对于电源侧有Е_в＞U_dв，受端有U_dи＞Е_и。

对于发电机—电动机系统也可以写出类似的关系。这是非常简单的关系，但是对于正确的理解逆变过程是必须的。阀在逆变器和整流器中都是一样的，起到可以实现快速响应的开关作用。问题在于，当相应的受端系统相间电压达到最大值时，为了使确定的阀对应导通；除此之外还必须保证阀换向的条件。

逆变器中阀的换向可以是利用受端系统的电压实现的。这样的逆变器被称为有源逆变器，其与无源逆变器的换向是有区别的。无源逆变器的换向是以其他原理为基础的，可以工作在无其他交流电压源的网络中。

单桥式逆变器的等值电路与整流器的等值电路相类似（见图10.9），区别可能只是在于变流器阻抗以及系统等值阻抗和电动势的数值上。因此，对逆变器过程的描述也是以整流器的方程组（10.25）和（10.28）为基础的。

变流器从整流器状态变换到逆变器状态，可以通过将控制脉冲的角度向右侧移动、超过90°-γg/2来实现。这对应于阀导通时刻向电压正弦半波的反方向切换，如图11.2所示。

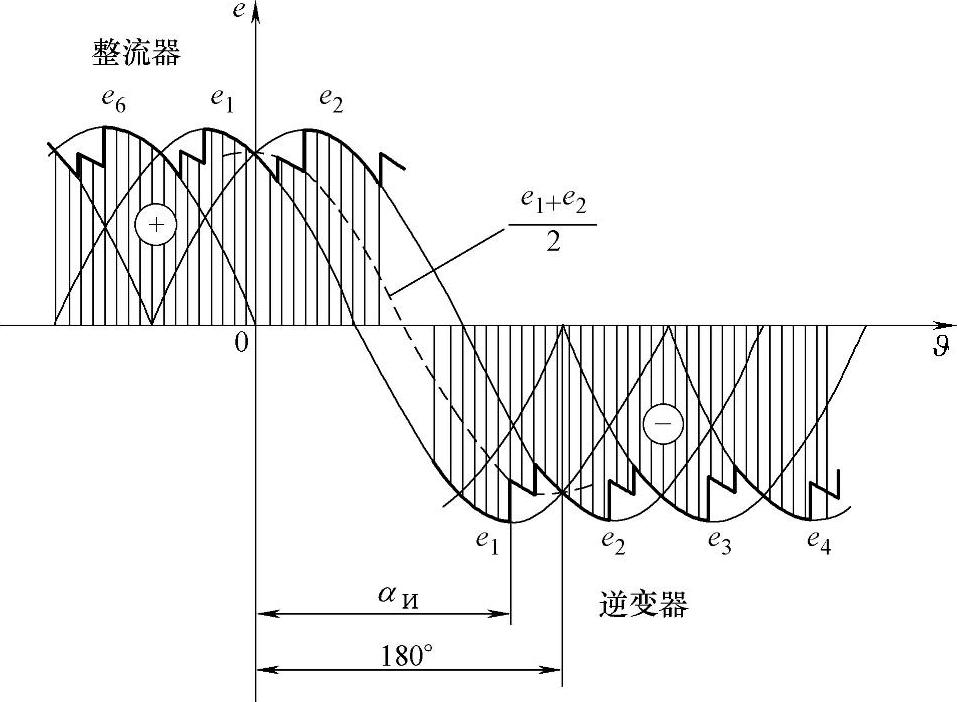
图11.2 整流器切换到逆变器状态的时间曲线图

下面详细分析逆变过程中阀的换向过程。

如同整流器，在此，电流由上一个阀过渡到下一个阀是根据两相短路实现的，两相短路在阀导通时是依次产生的。这个短路电流的方向是使阀结束工作时电流减小到0，而在投入工作时增加。换句话说，它是由超前的相（如A相）指向滞后的相（如B相），即在前面一相电动势高于后面一相电动势的时间段内。

对于阀1和2处于工作状态的一些时间段，当（90°-l/2）<ϑ<180°时，从式（10.25）和（10.28）中有：

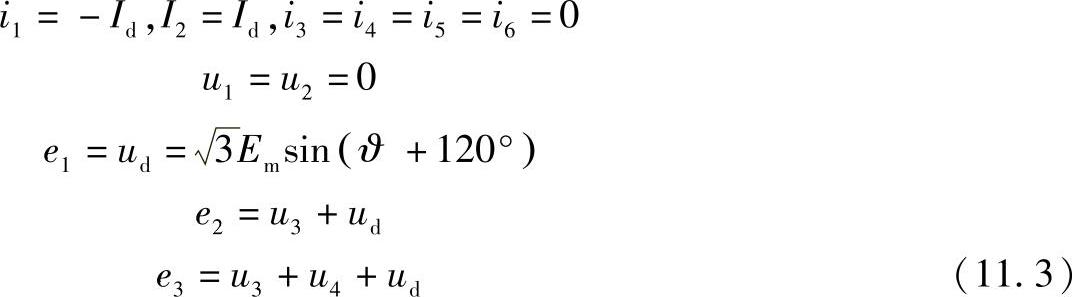
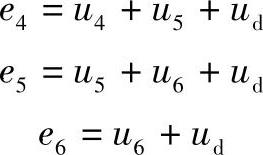
对于整流器也可以得到类似的方程组。但是在此区别体现在，因为J>90°，整流电压u_d的值将是负的。

当前阀3的电压在本时间段内大于0，即

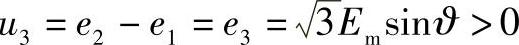
并且第三个阀准备导通。

如果在角度a_и所决定的时刻上，对阀3施加控制脉冲，阀3导通，并开始由阀1到阀3的电流换向。

其中重要的是，为了保持换向电流的方向，控制脉冲必须是当J<180°时施加（见图11.3），即在相电动势е_A和е_B左侧交点。换句话说，在逆变状态下应当满足条件

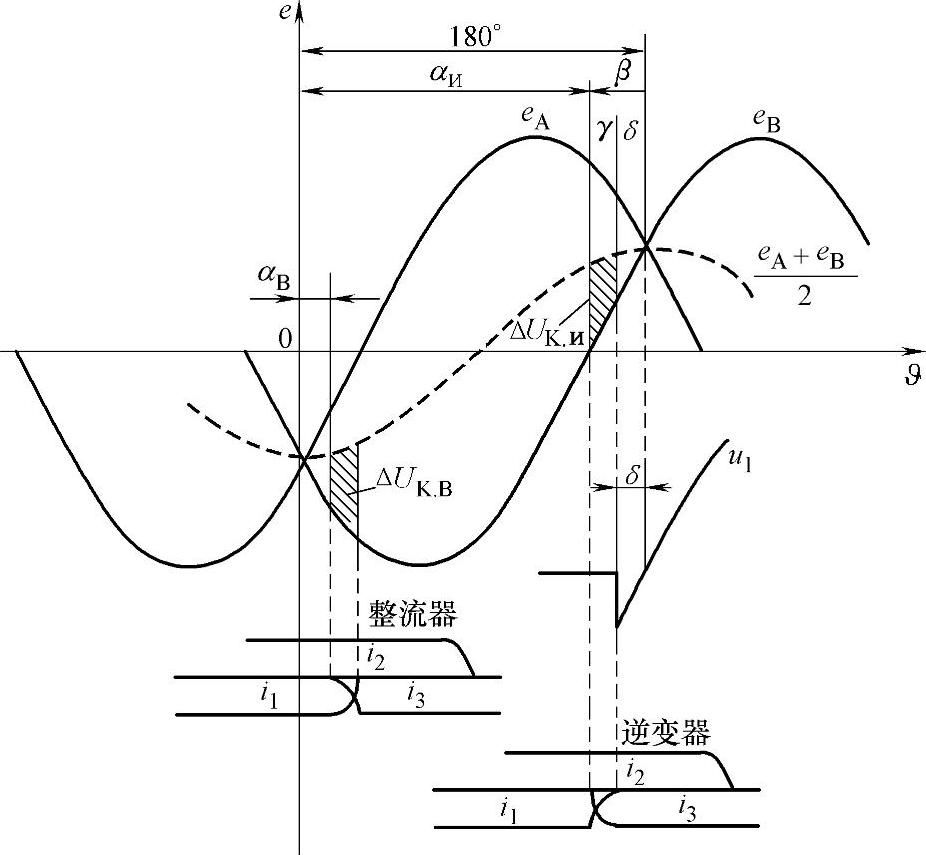
图11.3 逆变器中的换向过程

但是，通常逆变器阀的导通不是在角度a_и所对应的时刻上，而是b，β是按照超前相电动势交点的一侧计算的，相电动势是按照相对所采取的初始时刻轴位移180°。因此，此角度有时也被称为逆变器的超前角。

由图11.3有

β=180°-α_и （11.5）

以及 β=γ+δ （11.6）

当推导整流器换向过程的方程时，并不给定角度a的值。因为在逆变状态下，阀的导通是在0°≤J<180°范围内（与整流状态一样）。显然，早先所得到的方程对于逆变状态将同样适用。因此，对于逆变器换向阀的电流可以写成

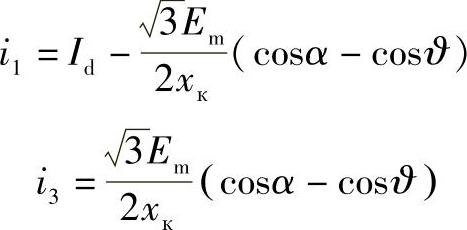
区别只是在于角度a的值和J的当前坐标。这种情况将反映在改变换向阀电流曲线的弯曲特性上。除此之外，整流电压的值在整流器换向过程中减小DU_к.в而在逆变器换向过程中增加DU_к.и，如图11.3和图10.20所示。

逆变器电流和电压的时间曲线图如图11.4所示。

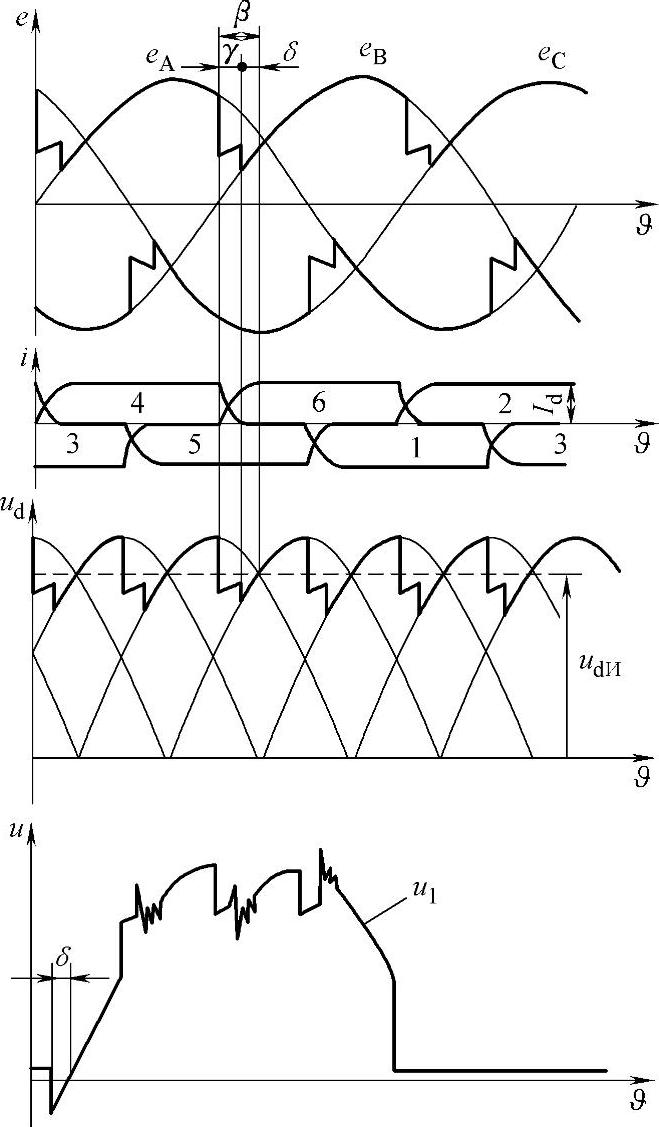
图11.4 逆变器电流和电压时间曲线图

为了确定逆变器换向角的值，使用方程（10.53），将角度b代入式（11.5），结果有

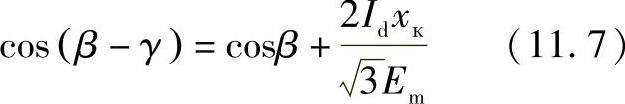
表达式（11.7）可以用来确定当给定的角度b不变时，逆变器的换向角。

计及关系式（11.6），由式（11.7）有

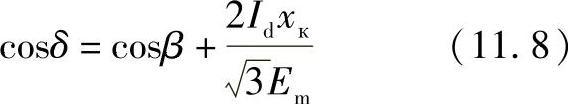
上述方程确定了晶闸管闭合角与角度b以及状态参数I_d和E_m的关系，即与负载电流和受端电动势的关系（或者是逆变变电站母线上的电压）。应当注意，方程（11.8）只是当b<60°时适用。这个方程可以用来确定当逆变器的闭合角d给定时逆变器的换向角。

计及（11.6），由式（11.8）变换后可以得到

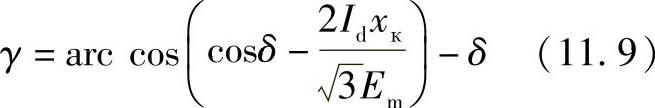
晶闸管的闭合角d是逆变器最重要的参数之一，它决定了当负载电流I_d增加以及受端系统电压降低时，逆变器工作的稳定性。电压急剧降低可能是由此系统短路引起的，破坏逆变器的工作。

为了解释此过程的物理本质，下面分析阀1闭合后其电压的变化特点（见图11.3和图11.5）。结束工作时阀上附加突变的负电压，等于

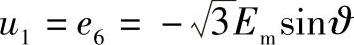
当ϑ=180°-d时为(www.xing528.com)

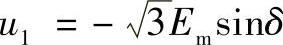
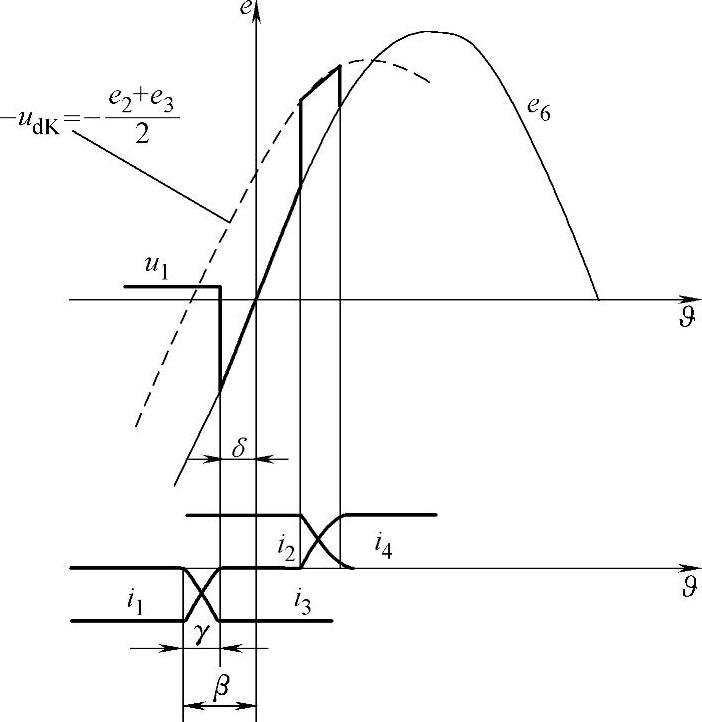
图11.5 逆变器阀1上的电压

在最初突变时，电压u₁是负的，然后开始增大，按照电动势e₆的正弦曲线变化，当J=180°时过0并且改变符号。

阀上电压为负的时间间隔，以晶闸管的闭合角d来度量。当阀闭合后，第三电极的电介质强度和可控性不能瞬间恢复，必须经过一段时间耗尽晶闸管上的充电电荷，这个时间是由晶闸管的结构和规格决定的，对于现代的大功率晶闸管可以达到250～300ms（电网频率的4°～6°）。对于最新的晶闸管系列，这个时间大概为30～40ms甚至更小。

随着角度b的增加，晶闸管的闭合角通常设置得比上述值要稍微大一些，实际当中要满足条件d＞d₀，其中δ₀为晶闸管闭锁能力恢复的角度。对于现代的高压阀式晶闸管，闭合角等于15°～18°。角度d的进一步增加是不合理的，因为这将导致逆变器电气性能的恶化。

如果在此时间之前，由于某种原因闭合晶闸管上的电压变成正的，则重新导通，从而导致事故的产生，这被称为单相逆变器的翻转。

下面以阀1为例分析这个过程（见图11.6）。

如果阀1没有关闭，仍继续工作，那么回路中的阀1、3、2也是工作的，在由整流器提供的整流电压作用下逆变器回路有电流流过。此时，线路的正极连接到桥阀阳极组的阳极上，负极连接到阴极组的阴极上。

通过工作阀1正电压施加到阀4的阳极上，并且阀4准备导通。阀3导通后经过60°，控制系统施加控制脉冲到阀4上，阀4导通。结果是阀1和4之间产生了逆变器桥极间的短路（见图11.6），因此桥极—极的电压以及其功率突变到0，对于受端系统可能产生负面影响^[1]。

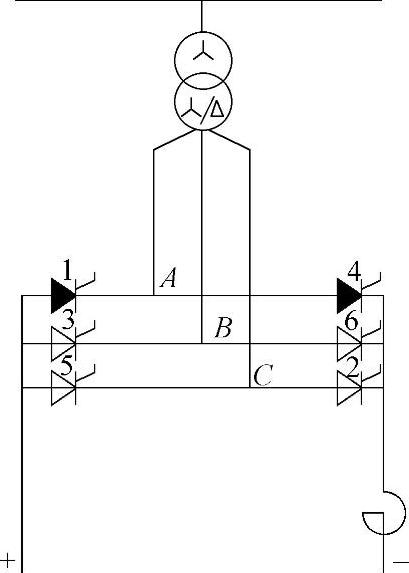
图11.6 单相逆变器翻转

引起逆变器翻转的原因，可能是如下因素：

由于受端系统电压的降低或者工作电流的增加（无自动控制系统的情况下），可能产生阀换向延迟；

1）受端系统不对称短路时的相突变；

2）受端系统不对称短路时的相位突变；

3）阀控制系统的工作中断。

下面详细分析这些原因。

角度δ与负载电流I_d以及受端系统电动势（或者逆变变电站母线电压）的关系，由表达式（11.8）决定，这些关系对于不可控逆变器（b=常数）如图11.7所示。

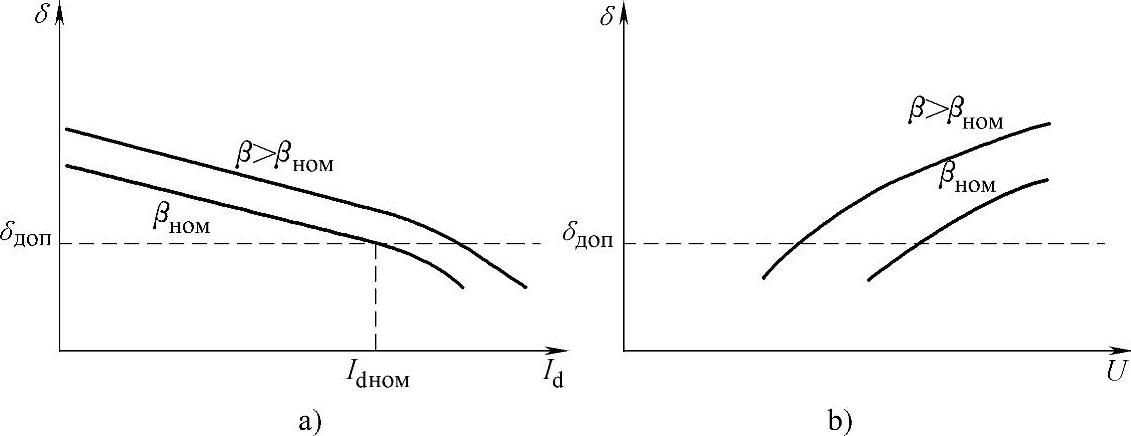
图11.7 角度d与电流I_d a）和受端系统电压U b）的关系

由图可见，负载电流的增加或者受端系统电压的对称降低，会导致晶闸管闭合角度减小到不允许的值，原因在于换向角度的增加。在一些情况下，当受端系统电压严重降低时，两相短路的整流电流可能非常小，阀终止工作时的电流通常不会降低到0。它只是略微减小，然后增大，并且阀1仍然在工作，此后当阀4导通时逆变器翻转。

相位突变是在受端系统不对称短路时产生的。在单相短路时，假设A相电压降低，结果是相电压u_A和u_B的交点向左侧移动（见图11.8），由此当b=常数时，角度d的突然降低可能导致逆变器翻转。

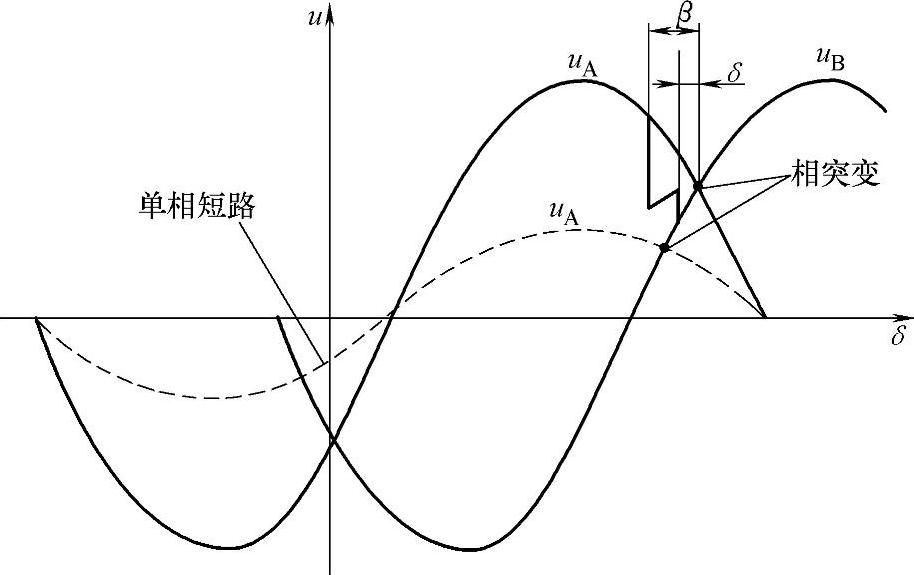
图11.8 受端系统单相短路时的相位突变

当阀的控制系统不能正常工作时，控制脉冲没有依次施加到阀上（在此是阀3）。因此阀1和3之间的换向过程并没有开始，并且阀1仍然在工作。阀4导通后回路中的逆变器翻转。

上面分析了单相逆变器翻转可能的原因。可以看出，当引起翻转的原因消失后，逆变器回到正常工作状态。为了不使逆变器翻转，必须在所有的状态参数发生偏差时保证阀的闭合角不变，即满足条件

d=常数 （11.10）

这个条件可以通过调节闭合角来实现：改变状态参数，或者是直接改变角度d的值，从而对角度b的变化产生影响，并且改变阀的依次导通时刻，以满足条件（11.10）。

闭合角度调节器以两个原理为基础。第一个是使用了当b=常数时，由方程（11.8）所决定的调节策略；第二个是使用直接测量的角度d，为此测量阀电流过零点与相应相电压交点之间的时间间隔，然后制定角度b变化的指令。在第二种情况下每个阀的角度b可能单独变化。

由上面的分析可以看出，角度b的变化范围处于下述范围内

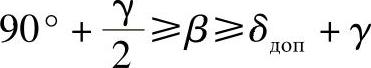
此时左侧的边界意味着逆变器过渡到整流器状态。

可见，实际上在角度β的整个变化范围内，逆变器只能工作在状态2—3下。当电流严重超出输电线路的额定电流以及负载允许电流时，而在整流状态边界附近的工作则是例外。

当将aи=180°-b代入时，不可控逆变器的外部特性方程可以由式（10.58）得到，

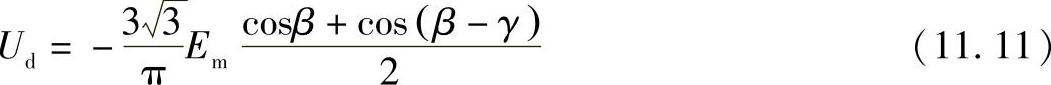
由式（11.7）将cos（β-γ）代入，最终得到

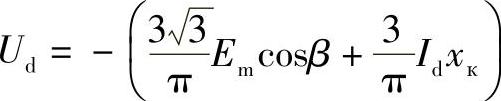
这个方程前面的负号说明，逆变器产生反电动势。这个方程的特点是线性的，并且分布在负半轴。但是为了使整流器和逆变器的工作特性相结合，以及确定其协同工作点，逆变器的工作特性通常分布在正半轴。此时负号消失，方程变成

当b=常数时，逆变器的外特性符合方程（11.12），如图11.9所示。对于任意的其他具有内部反电动势的直流设备，逆变器的外特性具有上升的特点。

式（11.12）的第一项是逆变器产生的反电动势，第二项是逆变器内部阻抗上的电压损耗，这个阻抗与受端系统和连接到直流侧的逆变变压器等值电抗是一样的。

当b＜60°时，逆变器整流电压瞬时值曲线如图11.3和图11.4所示。可以看出，与整流器的区别在于，换向过程中电压的瞬时值是相应电动势曲线的和。因此，方程（11.12）的第二项是正的，特性曲线上升。

对于闭合角不变的逆变器，即当角度b变化时，外部特性方程可以由方程（11.8）将cos b代入（11.12）得到，变换后有

与不可控逆变器的区别在于，d=常数的可控逆变器外特性是下降的。

当b在0～60°的范围内变化时，方程（11.13）是直线，是不可控逆变器特性曲线族的边界点。事实上，如果逆变器工作在b=常数时，负载电流的增加将导致角度g增大，并且造成角度d减小。在某些给定的闭合角下，进一步地增加负载电流是不可能的。因此，外特性在角度d给定时只能到达边界直线上（见图11.9）。

整流器和逆变器的综合外特性显示（见图11.10），改变控制角可以平稳地将变流器由整流器状态过渡到逆变器状态（或者相反）。在某些角度a下，过渡到另外一个状态是由变流器的工作电流决定的。例如，当工作电流增加并且控制角不变时，整流器可以改变电压的极性，即过渡到逆变状态，而当电流减小时变流器重新过渡到整流器状态。这个特性决定了换向角对变流器电压幅值和极性的影响。

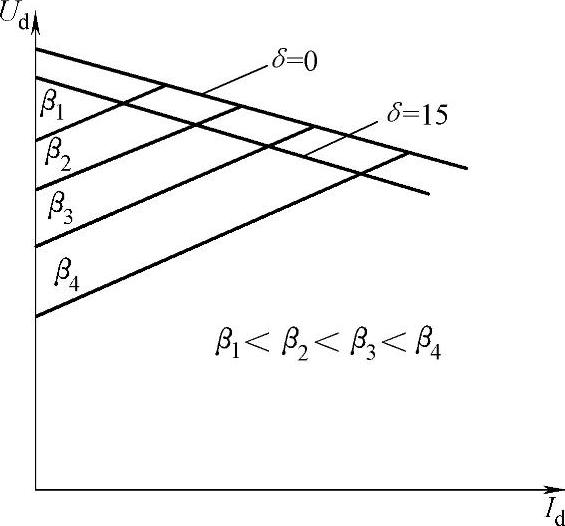
图11.9 当d=0及d=15°时，逆变器的外特性

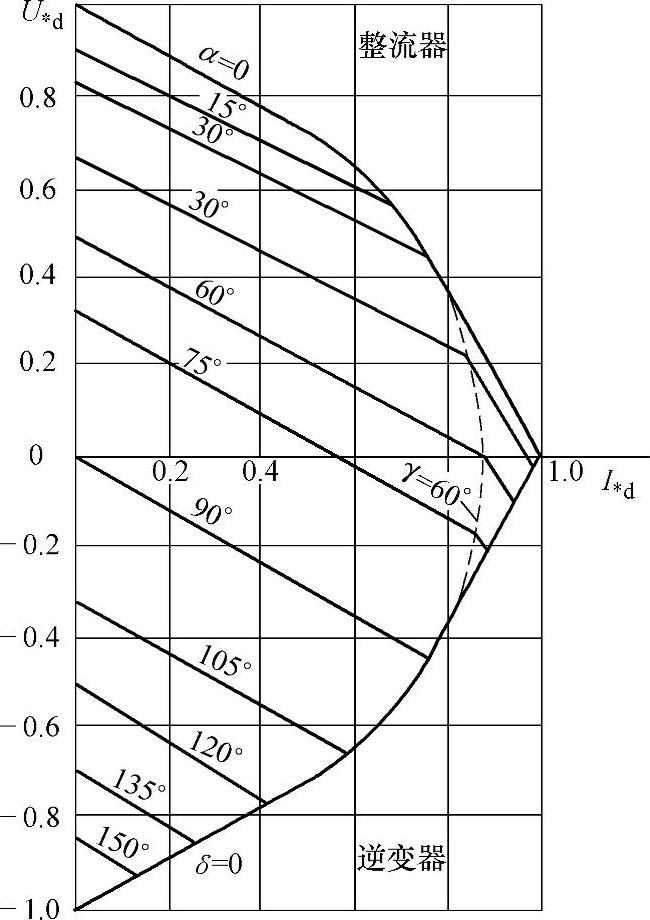
图11.10 整流器和逆变器的综合特性