超高压远距离输电小电流状态优化

当整流器的负荷较小以及当整流电流为I_d时，支路中的电流同样较小（达到其额定值的5%），从而可以忽略阻抗x_к中当相电流变化时产生的感应电动势，即采取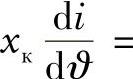0。此时方程（10.28）有如下形式：

对于上面所得到的电流方程（10.25），在此也是适用的。

如果采取x_к=0，也可以得到类似的结果，这可以合理地解释整流器的工作原理，并且得到此时的简化表达式。

方程（10.29）是非线性的代数方程，因为理想阀的伏安特性是非线性的（图10.10b），按照阀的分段线性特性将整个过程分解为一些独立的时间段在此仍然适用。在一个电网频率周期内，整流器桥回路工作原理以及各个阶段特性的解释如图10.11和图10.12所示。

在图10.11中列出了每一个时间段内工作阀的配合、回路中有效的相电动势、以及相电流和直流电流的方向。在此图上，粗线条表示在本时间段内流过电流的回路元件；在本时间段内不工作的回路元件以细线条所示。下面的图列出了以电网周期频率弧度表示的每一个时间段的时间范围。

应该注意的是，在任何一种工作阀的配合中整流电流I_d的方向是不变的，同时相电流的方向向反方向变化。电流I_d方向不变的特性证明了，在所有的工作阀的配合中可以保持整流器的极性。同时相电流方向的变化说明，在变压器绕组中（在此并未显示）流过交流电流。

同样要注意以下情形。引起整流器（不同于逆变器）回路各个支路流过电流的原因，是交流网络的电动势。

在图10.12中列出了整流器工作在状态2时电流和电压的时间曲线图，各个相的电动势、整流电压、阀电流、A相电流、阀1上的电压被指定。为了解释发生在整流器中过程的物理本质，适当地结合图10.11和图10.12的数学描述来进行分析。

下面继续分析状态2。为此，必须选择起始时刻，在原理上时间起点是可以任意选择的，但是按照一定的工作阀之间配合选择会更加方便。假设阀1和2处于工作状态，为此时间起点选择A和B相电动势正弦波在负半周交叉时刻更加合理，而C相此时达到峰值，如图10.12所示。

根据定义的时间起点，校正相电动势向量，其方程具有如下形式：

此时，根据表10.2电动势е₁-е₆可以描述为如下方程：

图10.11 变流器桥中阀对的工作顺序

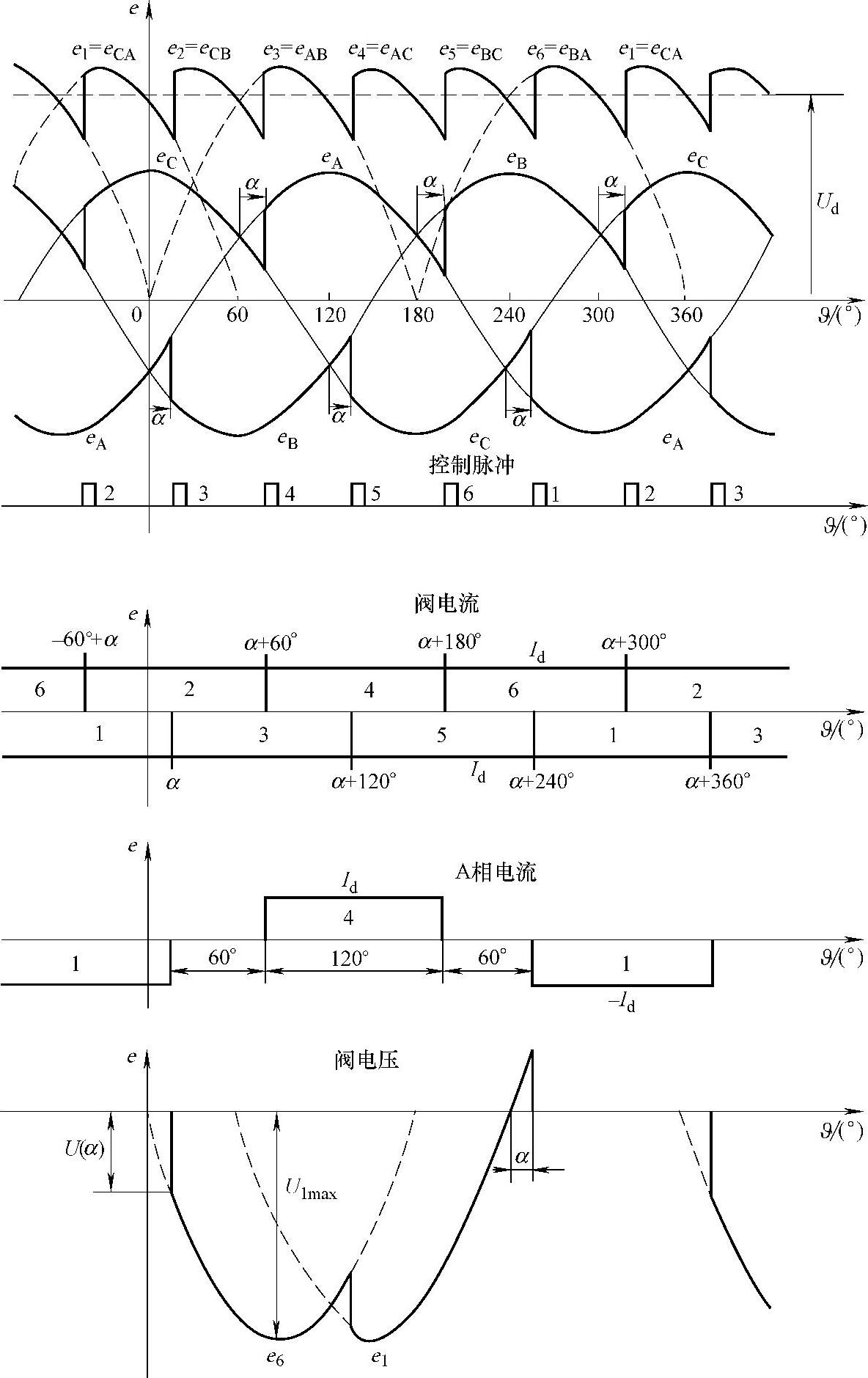
图10.12 状态2的时间曲线图

与式（10.30）和式（10.31）相对应的相量图如图10.13所示。

在阀1和2工作的各个时间段内，阀上的电压等于0（u₁=0，u₂=0），非工作阀的电流同样等于0（i₃=i₄=i₅=i₆=0）。据此，由式（10.25）和（10.29）可以得到：

i₁=I_d，i₂=I_d

i_A=-I_d，i_B=0，i_C=I_d （10.32）

e₁=u_d

对所分析的时段，整流电压是A相和C相之间的线电压，即工作阀所连接的那些相电压，而这些相的电流等于整流电流，符号是反向的。

由方程（10.29）可以得到非工作阀上的电压，并且确定在下一个时间段内将要工作的阀：

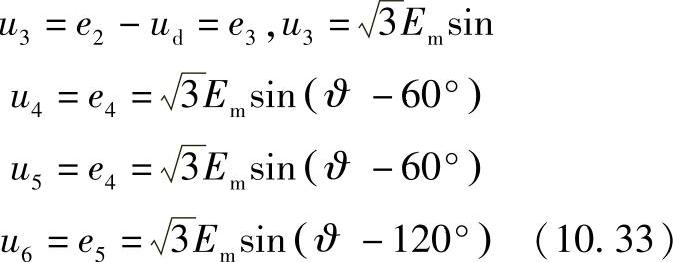
图10.13 变流器回路中有效的电动势相量图

由此可以看出，在从0～60°的时间段内，可以投入工作的只有阀3，因为此时电压u₃>0。实际上由图10.11a也可以看出，在被分析的时间段内阀3处于电动势e_A和e_B的作用下，B相电势施加到阴极上，而A相电势经过工作阀1施加到阳极上。如图10.13所示，在此时间间隔上e_A＞e_B。换句话说，阳极电势要比阴极电势大些，阀准备启动。所有其他阀上的电压是负的。

如果在一些由角度a所决定的时刻上，在阀3上施加可控脉冲，那么其将投入工作。此时阀启动的两个条件被满足，在启动之前瞬间阀上的电压将等于

回路中的电流是很小的，因此储存在每相电感中的电磁能量也是很小的，当х_к=0时完全不存在。此时阀3开启，电流由阀1瞬间切换到阀3上。阀1关闭，A相电流跃变到0，B相电流同样跃升到值I_d，阀2和3持续工作（见图10.11b），这个时间周期的长度是60°，从a到a+60°。

对于新的处于工作状态的阀组合，存在如下方程：

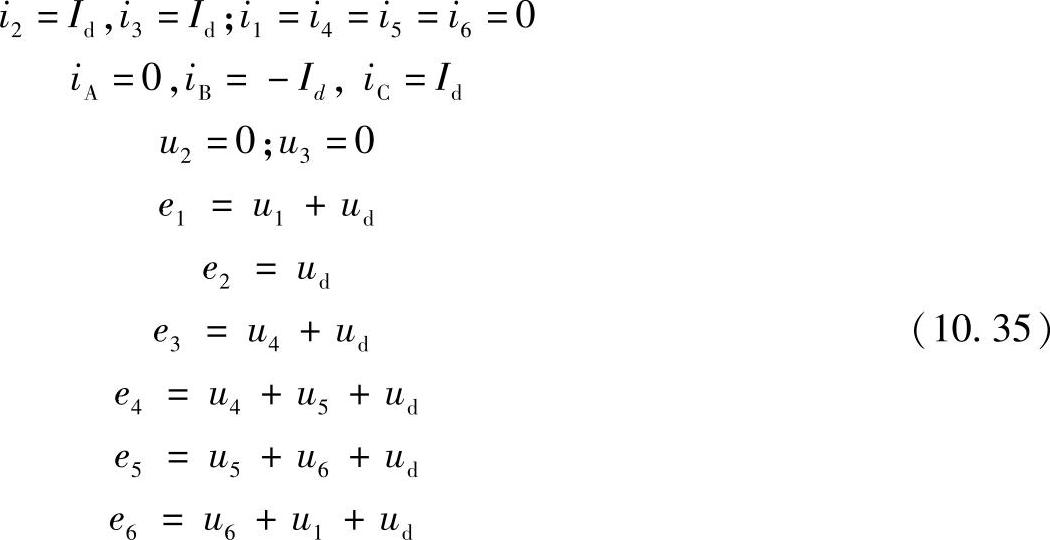
其中，整流电压由电动势е₂（e₂=u_d）决定。

已经结束工作时的阀1上的电压等于u₁=e₁-e₂=e₆ （10.36）

在阀1开启瞬间，当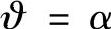时，施加到其上的跃变电压为

由图10.11，b～e和10.12可以看出，在没有导通时，阀1上的电压是由被连接到阴极上的电动势е_А、电动势е_В和е_С的差形成的，e_B和e_C经过工作阀3、然后是5施加到阳极上。由此，在没有导通时，此状态下阀1上电压的最大值，是由相间电动势е₆和е₁的幅值决定的，如图10.12所示。(www.xing528.com)

反向电压和其他阀也有类似的形式。

由方程10.37可以得到，在结束工作的阀上，反向电压跃变的最大值将发生在a=90°时。考虑到此时同时存在最大的电压变化率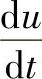（理论上等于无穷大），则在此状态下阀的工作条件最恶劣，应该在高压晶闸管阀的结构设计中考虑。

由方程（10.35），此周期内其他不导通阀的电压等于：

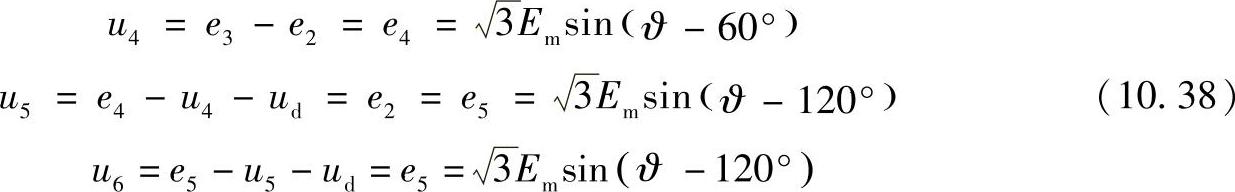
由方程（10.35）（10.38）和图10.12可以看出，当ϑ>60°时只有阀4准备导通。如果在ϑ=60°+a瞬间其上施加控制脉冲，其被启动并且瞬间由阀2换向到阀4上。阀3和4仍旧是导通的（见图10.11c）。再经过60°，控制脉冲被施加到阀5上，并且由阀3换向到阀5（见图10.11d）。还要再经过60°，阀6被投入（10.11e），以此类推。

当控制脉冲按照顺序施加到阀上时，每经过60°都会有规律地重复这个过程。

由时间曲线图可以看出（见图10.12），在每一时刻的阴极组上，只有电压达到最大值的那一相处于工作状态；而在阳极，电压达到最小值的那一相处于工作状态。换句话说，有一对阀处于工作状态，其中的一个在阳极达到最大电压，而另外一个在阴极达到最小电压。任意时刻的整流电压都是被工作阀连接的这些相的相间电压建立的。

相电流是间断的，在连接到此相的阀工作时，电流等于I_d，在其他时间上等于0（见图10.12）。

那么，整流桥在本质上是快速动作的换向装置，在一个周期内产生6次换向，即每经过3.33ms换向一次。因此，这种接线也被称为变结构接线。其每一个状态都对应一个方程组。

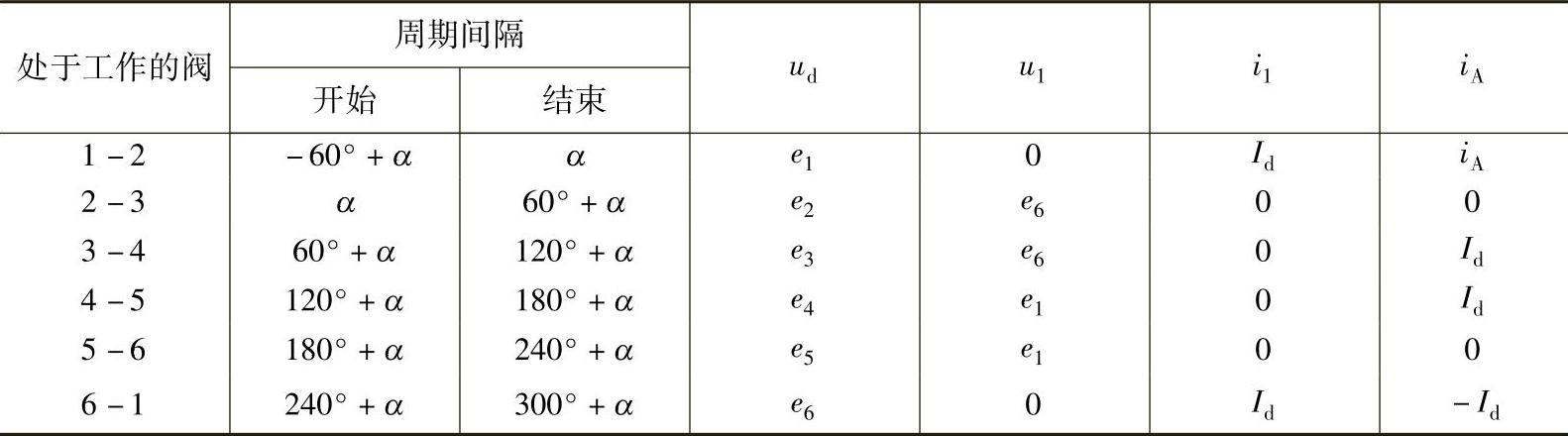
对于状态2下整流器回路其他部分的电流和电压值如表10.3所示。

表10.3 不同电网频率周期内整流器回路元件的电流和电压值

因为在变流器和线路之间连接有平滑电抗器，线路的极电压不是由瞬时值决定的，而是由整流电压U_d的平均值决定的。为了得到此电压，必须采取一个循环周期Т内的时间间隔：

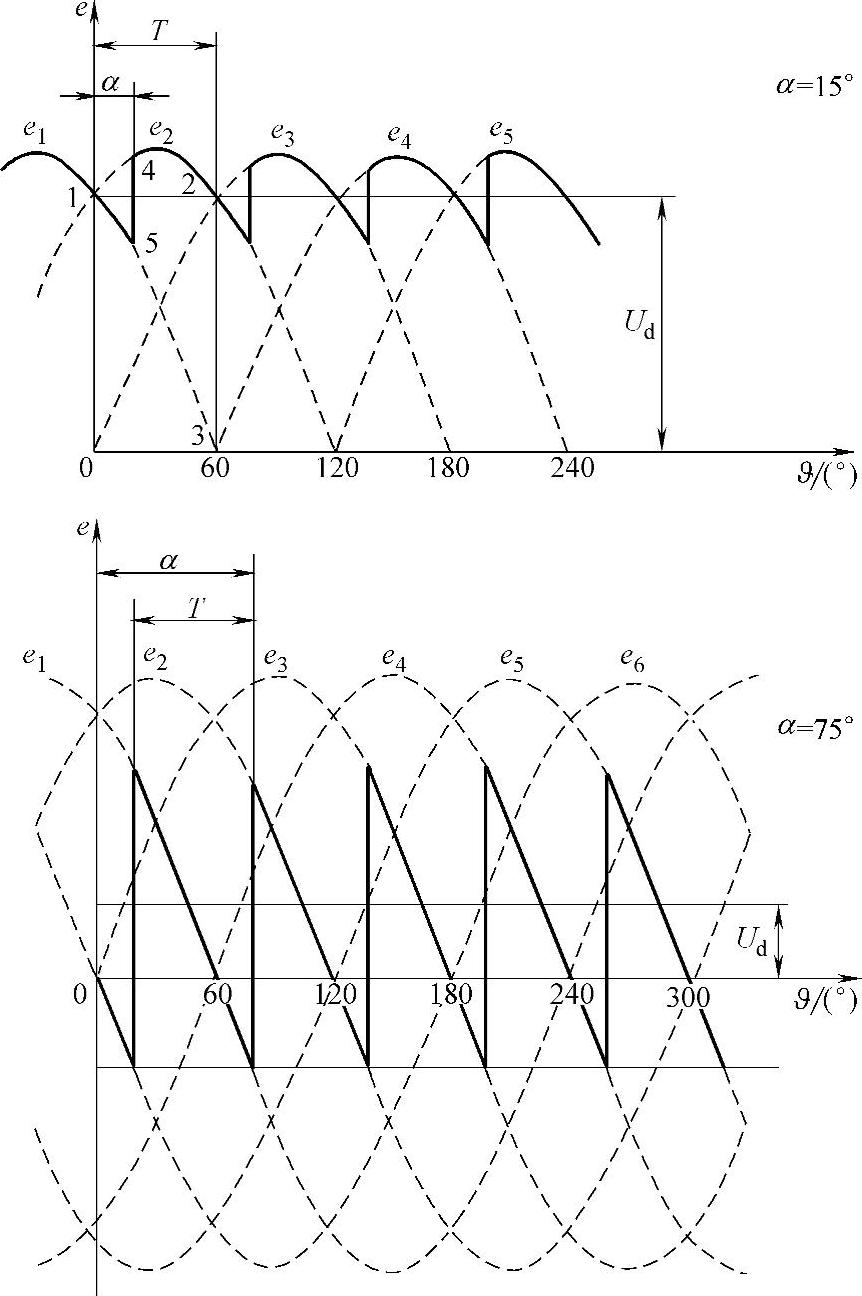
图10.14 当角度a取不同值时状态2下的整流电压

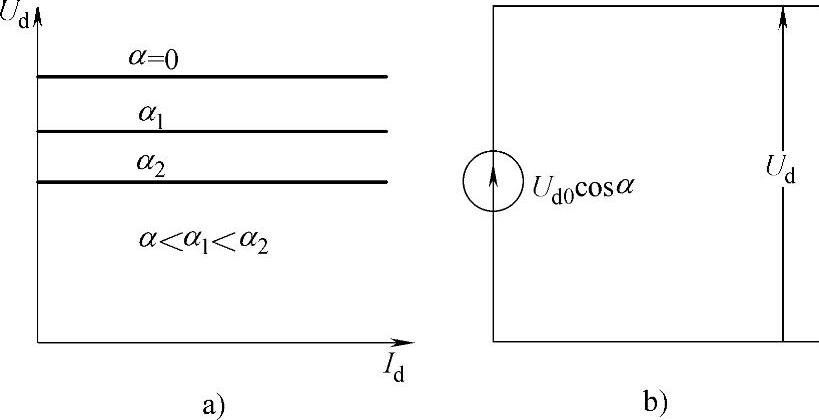
图10.15 状态2下变流器的外特性（a）及其等值电路（b）

将式（10.31）中的e₁和e₂代入，计及T=p/3，得到：

U_d=U_{d 0} cosα （10.39）其中

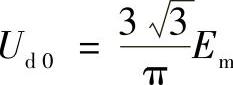
由此可以看出，当角度a由0°～90°变化时，整流电压由0～U_{d 0}变化。

角度a对电压U_d的影响如图10.14所示。取决于角度a的面积被从对应于不可控整流器的面积（正弦波顶部）中分离出来，结果是降低了整流电压U_d的平均值。当a=15°时，从正弦波е₂中分解出来的面积以符号1-4-5表示。在图10.14中同样列出了角度a=75°时的整流电压瞬时值和平均值。后一种情况整流电压的平均值要比前一种情况小得多。

方程（10.39）说明，在上述状态下整流电压与工作电流I_d无关，变流器的外特性U_d=f（I_d）此时与横坐标轴平行。当角度a增大时，其相对横轴平行，向下移动。变换到直流侧、以及相应此特性的整流器等值电路如图10.15b所示。

下面分析整流器支路中的电流。从状态2的时间曲线图（10.12）可以看出，桥中的每个阀在一个周期内只启动一次，此时流经阀的幅值等于I_d、长度为120°的矩形单极电流。阀的平均电流是其最重要的特性之一，此时等于

任一相的电流是由连接到此相上的阀电流决定的，A相电流由阀1和4决定，相互之间相差180°角度。此时阀1的电流将变成负的，因为它与所采取的相电流正方向（见图10.11）是相反的；而阀4的电流是正的，即与此方向是一致的。

在图10.16中列出了A相电流、A相电流基波和电动势e_A的时间曲线。相电流是由有不同极性的直流电流分段组成。

图10.16 A相电流和电压的时间曲线图

A相电流的有效值可以被用来计算整流桥的引线和变压器阀绕组，有如下的公式：

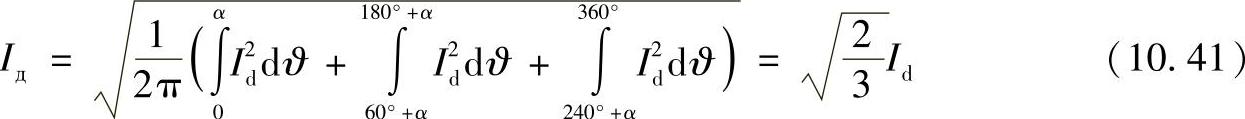
对A相电流和电压时间（见图10.16）曲线的分析，可以得出如下结论：

在桥和阀绕组的各相中流过符号变化的、相对于横坐标对称的电流，这说明其中没有能够引起变压器铁心磁化的直流分量（在额定状态下）。

相电流有明显的非正弧特点，换句话说，其含有对供电系统不利的高次谐波成分。从而必须采取补偿措施，抑制这些高次谐波电流。

基波电流相对本相电动势位移角度j₁，等于滞后侧的角度α。

电流滞后说明，整流器需要从电网中吸收由角度α决定的无功功率，此无功功率可能与有功功率相当。因此必须采取措施，以保证换流站母线上的无功功率平衡。

改变角度α，可以改变变流器从电网中吸收的无功功率和有功功率的比例。当α＞90°时，有功功率的符号变成负的。这说明，变流器变成了发电机，即过渡到了逆变器状态。无功功率的符号此时不变，意味着还是从电网中吸收无功。