深入探究10.4变流器的数学模型

任何数学模型都是为了解决一些问题而建立的。下面推导变流器电磁过程分析中所用的数学模型，以及借助于此数学模型得到变流器的主要特性。如果需要研究的是直流换流站和直流输电线路的系统特性，那么还需要使用以变流器模型为基础的其他模型。

在图10.9中设定电流的正方向，认为与阀电流方向一致的为电流正方向。可以从任意一个阀开始编号，但主要是要遵守其导通的顺序，与此相对应来进行编号。在此采取独立变量J=wt，使得有可能以电角度和弧度表示一个电网频率周期内所感兴趣的时间断面。

在图10.9所示回路中，与基尔霍夫定律相对应，可以得到下列方程：

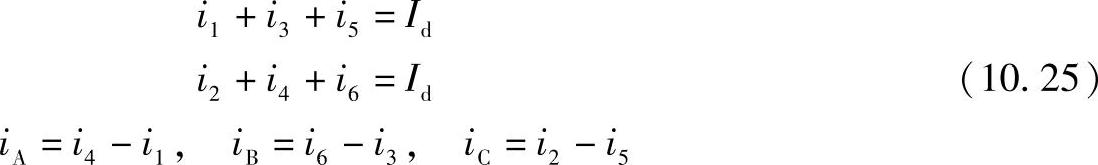
环绕由阀1和2所形成的回路以及电动势е_А和е_С，使得环绕方向与这些电流的方向一致，得到：

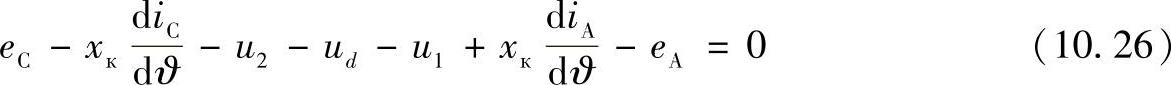
其中，x_к=x_с+x_т；

u₁，u₂——阀1和2的电压。

当存在谐波补偿装置时，能够维持变流站母线电压为正弦波和常数，x_с可以忽略，况且通常x_с≪x_т（考虑这个因素是为了推论一致性）。

通过阀电流将相电流分解出来，并且将电动势移到方程的左侧，而剩下所有的项在右侧，得到：

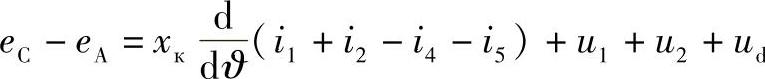
如果采取类似的环绕方向，每一次都按照同样的方式选择回路和环绕方向，为了使阀对按次序加入回路中，1-2，2-3，3-4，…，6-1，可以得到：

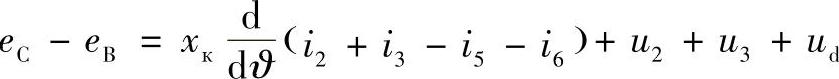
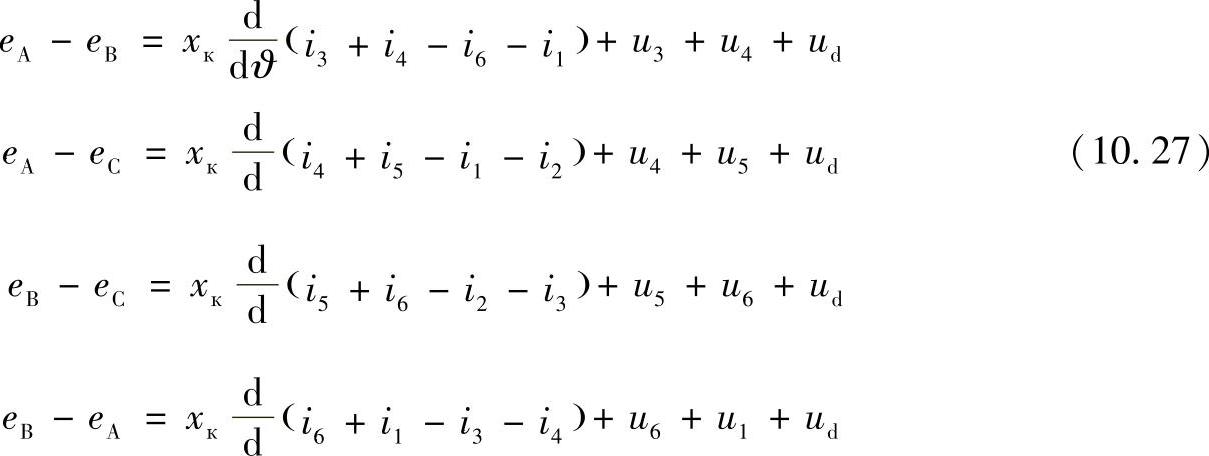
在上述方程的左侧是电动势差，在相对应的阀对工作时将附加到整流电流回路上，形成整流电压。(www.xing528.com)

为了简化方程（10.27），在方程的左侧以一个等值电动势替换相电动势的差，即用е_С-е_А=е₁；е_С-е_В=е₂等来表示。相应于其回路的符号如表10.2中所示。

表10.2 按照阀的工作次序变流器回路有效的电动势

按照表10.2，采取回路中的有效电动势符号，可以得到：

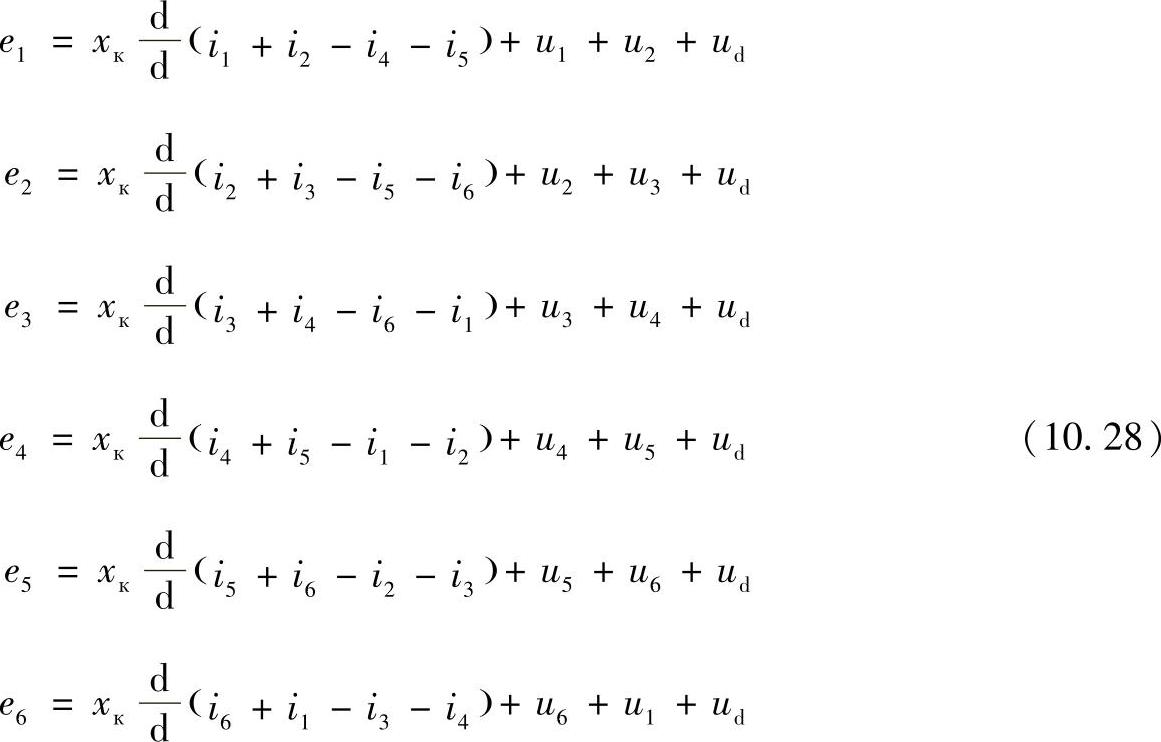
电流和电压方程组是完整的，可以在采取上述假设条件下描述所有的三相变流器桥回路中的过程，以得到任何一个瞬间每一个元件上的电压和支路电流。

应该说明，在方程（10.25）～（10.28）中使用了电流、电压和电动势的瞬时值，其有效值和平均值将在下面解相应的方程得到。

方程（10.28）是非线性的，因为其中包含自身的阀电压u₁-u₆，阀电压通常是电流的非线性函数（见图10.10）。由此，求解上述方程是很困难的。以分段线性化的曲线替换上述阀的实际特性，对于此特性的每一个分段可以得到线性常系数的微分方程。

为此，整个过程被分成一系列的时间段，每一个时间段都有确定的阀组合。因为阀被认为是理想的，所有工作的阀都被表示为闭合开关的形式，不工作时就是断开的。结果是在每一个时间间隔上的过程都被描述为线性的微分方程集合。但整体上的过程还是非线性的。因为分段线性特性的拐点表示的过渡时刻，与回路元件的电压和电流密切相关。

对于每一个被线性微分方程所反映的时间间隔，在解这些方程时要求解积分常数。积分常数可以根据时间间隔的边界条件得到，即按照上一个时间段终点等值电路元件中的电流和电压值得到，这个方法被称为分段拟合法。

应该说明的是，现在也有其他的变流器电路分析方法（差分方程法，谐波分析法，转换函数法等等），但是分段拟合法被用得最多，也是最直观的表示方法。

如果过程是周期性的，只要针对其中一个周期进行分析就足够了，并且所得到的解推广到整个过程中。对于单桥式变流器，循环周期等于60°，因此只是针对这个周期内所包含的时段，求解所得到的方程就足够了。

方程（10.25）、（10.28）及其解法不仅适用于整流器，对于分析单桥式变流器的逆变状态也是适用的（下面分析这两个状态）。