单桥式变流器等效电路分析

由上述内容可见，变流器是直流换流站和输电线路主要和最重要的元件，它们的特性在很大程度上决定了输电线路和换流站本身的优缺点和性能。因此，为了把直流输电线路和换流站做为电力系统的元器件来研究，必须研究变流器的特性和可能的工作状态。为此必须对变流器中的电磁过程进行分析，得到回路元器件的电流和电压方程，并在此基础上得到决定其工作状态的变流器内部的电特性和其他特性。

现代的换流站都是以多桥变流器为基础构成的，连接与大地和电极之间桥的数量从2～4个不等。这些变流器的数学描述非常复杂，必须在专业课中进行分析和研究。为了简便，可以只针对一个桥进行分析，因为所有的桥都是完全相同的，从而多桥回路的特性可以做为单桥回路特性的综合。如果忽略邻近桥之间的相互影响，这样的假设是合理的。

不同桥之间的相互影响可能出现在，当所有桥的送端（整流器）和受端（逆变器）系统等值为一个总阻抗时。不同桥之间相互影响的本质在于，在一些工作状态下，阀换向时（如下所示）相邻桥中的两相短路电流可能相互叠加，结果导致交流变电站母线电压发生歪曲，使得阀的工作条件改变。

但是这种桥之间的相互影响也可能主要是在变流器过负荷时产生，不具有控制系统作用时直流输电线路和换流站的特征。除此之外，变流站装设高次谐波过滤器，使得其母线上的电压是正弦的。因此，桥之间的相互影响可以被忽略，只需对单个桥进行分析。

通过带有双绕组变压器的双极输电线路参数来表示单个桥的参数（见图10.7）。此时符号“в”将对应于整流器，符号“и”对应于逆变器。所有的对应直流侧的电压、功率和电流值都具有下标“d”。

桥的功率P_dмв等于

其中 P_d——整个输电线路的功率；

N_мв——两个半回路中桥的数量。整流器桥的整流电压

其中 U_п-зв——整流器极—大地之间的电压。线路的极电流可以根据下式得到

因为桥是串联连接的，这个电流对于整流器、线路和逆变器的所有桥都是相等的。对于变压器—桥回路，变压器的全功率可以近似得到

S_тв=（1.2～1.25）P_dмв （10.10）

为了便于分析，将所有的量折算到变压器阀绕组的电压等级下，阀绕组的电压可以由变流器的外部特性方程得到，如下所示：

其中 x_∗тв——变压器电抗的标幺值；

整流变压器的变比等于

其中 U_св——供电系统的网络电压。

折算到阀绕组的变压器电抗可以按照下式计算

系统的等值阻抗和电动势可以通过两种方式来确定：可以借助于复杂系统等值的方法；根据已知的变流站交流母线短路功率S_кз求解。在此使用第二种方法。

折算到阀绕组电压等级下的供电系统等值电抗，被确定为

此时供电系统的单相等值电动势幅值可以由完整的整流器外特性方程确定

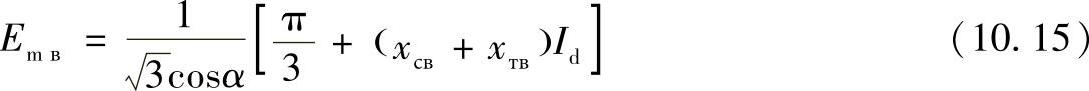
其中 a——整流器阀的初始启动角，可以等于5°～10°。

对于逆变器，可以使用类似的方程，并且计及线路的电压损耗。

加在逆变变电站输入端的线路末端极—大地之间的电压等于

U_п-зи=U_{п-з в}-I_dR_п （10.16）

其中 R_п——线路的极阻抗。

逆变器一个桥的电压可以被确定为

逆变变压器阀绕组的电压与整流器侧的电压是不同的，为

此时逆变变压器的变比等于

其中 U_{с и}——受端系统网络电压。

通常整流器和逆变器侧的变压器按照相同的生产工艺被制造成相同的功率，并且短路电压也是相同的。因此，逆变变压器阻抗的标幺值可以认为与整流变压器的相同。区别只是在于其变比，特别是在不同的网络绕组和阀绕组电压情况下。由此，折算到阀绕组电压等级下的变压器电抗等于

相应地，连接到逆变器的受端系统等值电抗等于

其中 S_{к и}——逆变变电站母线上的三相短路功率。受端系统单相等值电动势为

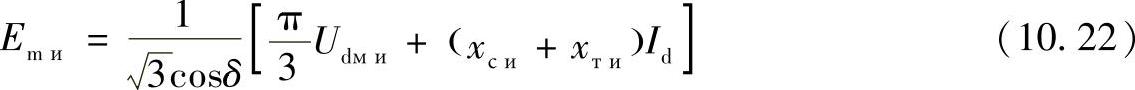
其中 δ——阀的启动角，可以取为15°～18°。结果是得到了不考虑过滤补偿装置情况下的整流和逆变桥等值电路元件参数。对于整流器和逆变器来说，等值电路的外型是一样的，区别只是体现在等值电路参数和状态参数的数值上。此等值电路如图10.9所示。

供电系统被表示为三相对称的形式，并且以等值电抗x_с后的正弦电动势来表示。变流变压器以本身的泄漏阻抗х_т.来表示，而系统和变压器的电抗，如同系统电动势那样，折算到一个电压等级上——变压器阀绕组的电压上。(www.xing528.com)

等值电路中不包括系统和变压器的电阻，以及设备的自身电容，也不包括交流回路的电阻，其原因有两个。首先，对于大功率的电力设备，这些电阻值与电抗相比不大；其次，在变流器的过程分析中有较小的过渡时间，以电网频率所对应的几度或者几十度来量度，其中并不出现电流自由分量的衰减。这种形式的大功率高压变流器设备自身电容对设备的工作条件将产生一定的影响，但是对变流器主要特性的影响不大，而计及它们将使得等值电路更加复杂化，并且提高了方程的阶数，使得分析更加困难。

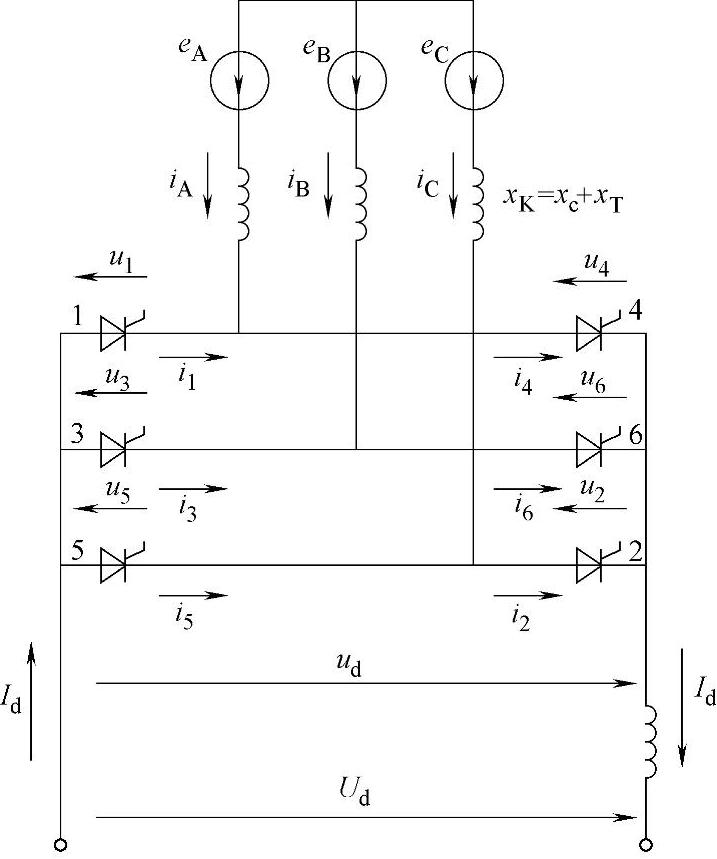
图10.9 变流桥的等值电路

高压晶闸管阀也是变流桥的主要元件。因此，为了正确地考虑等值电路中的阀，必须分析其特性。

前文已表明，高压晶闸管阀是单个晶闸管串联而成的链，因此其特性类似于单个晶闸管的特性。

晶闸管是硅栅，有两个稳定的状态：关闭状态下，其阻抗较大并且流过的电流较小；打开状态下，流过较大的电流。晶闸管是由圆柱形的、融合一些添加剂的硅锭制成的，其置放在薄板上（圆盘）。为了使所有制造好的晶闸管有相同的参数，硅锭被预先制成，也可以被称为中子合金，被粒子加速器中的中子流辐射。因此，添加剂在硅锭内均匀分布，使晶闸管具有一致的特性。晶闸管是4层的半导体p-n-p-n结构，有三个输出端：A—阳极；К—阴极；УЭ—控制极。晶闸管的伏安特性如图10.10a所示。

如果把外部电源电压正向施加到晶闸管上，即阳极为正极，阴极为负极，并且逐渐的升高电压。在晶闸管不加控制电流的情况下直到导通电压и_пер之前都是闭合的。此时外部特性的倾斜度取决于极小的泄漏电流，这个泄漏电流是可以被忽略的，即认为晶闸管的电流等于0。

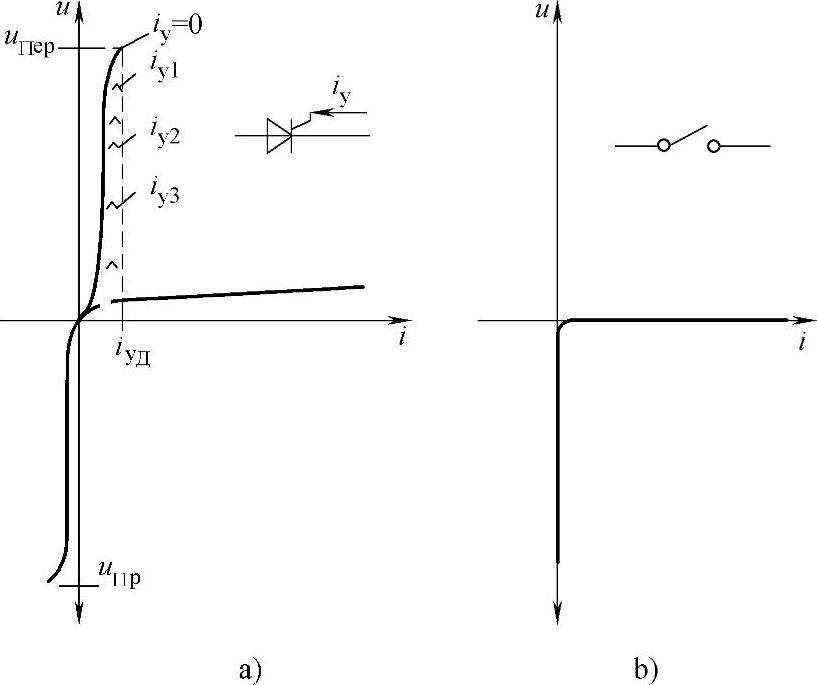
图10.10 晶闸管的电压电流特性a） 和开关（理想阀）b）

当电压达到и_пер时，一个晶闸管可能是几个伏特，晶闸管打开并且转换到导通状态，过渡过程是跳跃式的、具有雪崩特点。此时阳极和阴极之间的电压急剧降低。

如果控制极流过控制电流，对于大多数晶闸管来说，控制电流可以达到几十甚至是上百毫安（取决于控制回路参数），那么导通电压将降低，且控制电流的值越大，导通电压降低得越明显。在某个控制电流下，只要阳极电压超过阴极电压在晶闸管上形成电压降落时，晶闸管可以立即被开启。通常，此电流值也是由控制系统提供的控制脉冲。

当晶闸管开启后，控制极就不再起作用了，控制电流就可以被撤掉。因此，通常控制脉冲相对于电网频率是较短的，10°～15°。当其中的电流比阻断电流i_у（几百毫安）大时，被开启的晶闸管可以一直无限期地维持此状态。此时在全部工作电流范围内，晶闸管上的电压降落不超过1.5V～2.0V，比变压器绕组的电压低几个数量级。因此，在大功率高电压变流器的过程分析中，被开启的晶闸管阳极和阴极间的电压被认为等于0。晶闸管的这种状态构成了其伏安特性的水平部分。

如果由于外部原因，流过晶闸管的电流开始降低，当低于阻断电流时，晶闸管关闭。因为对于大多数型号的晶闸管，阻断电流只有额定值的百分之零点几，可以认为晶闸管是在电流过零时关闭的。

当晶闸管关闭后，必须经过一段时间，才能消除主要载体的电流以及恢复电气绝缘强度。对于高压晶闸管，这个时间大概为200～300ms，即工频周期的4～5°（电弧度）。对于最新研制的晶闸管，这个时间降低到了1°。

当晶闸管的极性发生变化时（阴极-正，阳极-负），晶闸管将维持关闭状态。其反向电流与工作电流相比是非常小的（伏安特性的下面部分）。当反向电压达到击穿电压ипр时，晶闸管中出现雪崩击穿，晶闸管报废。

对于最新型号的晶闸管，控制电流等于0时的导通电压与击穿电压大致相等。由图10.10a可以看出，晶闸管的伏安特性是存在严重非线性的。

为了避免晶闸管的不可控地开启和击穿，其参数应当与变压器绕组的电压以及桥回路正常和事故后状态下的工作条件保持一致。换句话说，在工作过程中，正向和反向上附加到晶闸管上的电压极限值，应当比导通电压和击穿电压小。

下面区分工作电压、重复电压和不重复电压的概念。工作电压是可能附加到晶闸管上的正弦电压幅值。重复电压是与正常工作条件下的正弦值不同的某个峰值、阶跃值。不重复电压是最大偶然电压值，例如，变流器回路事故状态下的值。

为了避免在非导通工作周期内随意投入所引起的事故状态下晶闸管的损坏，晶闸管参数的选择应当是，重复和不重复电压比导通和击穿电压小，通常由下式决定：

此时假设U_пер≈U_пр。

除此之外应当考虑到，晶闸管对电压变化率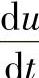和电流变化率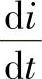是敏感的。如果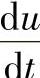超过晶闸管的允许值，晶闸管在没有控制电流的情况下或者是在不导通的周期内可能自动投入，从而引起变流器事故。因此，为了限制晶闸管的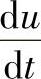值，需要设置分流的R-C回路。在由串联晶闸管构成的高压晶闸管阀（ВТВ）中，需要给每个晶闸管都分流。除此之外，为了保证电压在晶闸管链上的均匀分布，每个晶闸管还需要并联一个电阻。

如果电流的变化率超过允许值，可能造成晶闸管控制极区域内的局部过热，从而引起晶闸管损坏。为了限制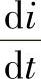值，需要在晶闸管链上串联电抗器。

可见，在高压晶闸管阀中的晶闸管有一系列的其他元件，但是它们都是起到辅助作用，其辅助特性参数并不对变流器桥的主要特性产生影响，因此在等值电路中可以不考虑。

除了以上所指定的参数之外，晶闸管还具有其长期流过的极限电流（一个电流周期内的平均值），这个电流值由硅锭的直径决定。

对于现代的直流输电线路和直流换流站，所应用的晶闸管硅锭的直径可以达到140mm，平均电流可以达到5.0kA，允许的反向电压为5.0kV～6.0kV，重复正向电压也可以达到这个值。同时，在流过工作电流时，晶闸管的启动电压为1.5V～2.0V。

如上所述，给出了以理想阀的分段线性化图形代替实际晶闸管的伏安特性（见图10.10b）。

理想阀具有如下性质：

1）同时满足以下两个条件时，阀可以被打开：阀的阳极和阴极之间电压相等或者电压差大于0（и_вент≥0）；控制极施加脉冲。如果其中的一个条件不能被满足，阀就不能被打开。

2）当其中流过电流（i_вент＞0）时，阀一直维持导通状态，直到阀所连接的回路电流降低到0时，阀被关闭。

3）严格来说，阀并不需要时间来耗散大量的电荷，其电气强度在其关闭后可以立即恢复。然而下面要考虑这个时间，因为晶闸管实际工作时这个时间还是较长的。

由此可以看出，正向极性上电压只有在其关闭后经过一段时间才能施加到阀上。

除了计及上面所提到的阀特性之外，同样需要考虑当晶闸管关闭后能够经受的、施加到其上的最大正向和反向电压。

那么，理想阀当其中流过电流时，可以以闭合开关的形式来表示，当其中的电流过零时以断开开关的形式表示。需要注意的是，无论对于理想阀还是实际的阀，都是非线性元件，如伏安特性曲线所表示的那样。从一个方面来说，正是由于这种特性，桥电路（或者是其他电路）才能变换电流；从另一个方面来说，非线性元件的存在使得阀中的过程分析复杂化，因为通常情况下解决非线性问题是非常困难的。在变流器回路分析时不得不使用一些手段，特别是分段拟合法，将在下面阐述。

在分析桥式变换回路时，其中一个最重要的假设是，整流电流无波动（I_d=常数）。理论上，只有当L_d=¥时才能有这种结论。但是经验表明，这个假设也可以在限制平滑电抗器电感的情况下实现：

х_d≥（8～10）x_т （10.24）其中

x_d=2pfL_d

同样所采取的假设还有忽略变压器的励磁电流，因为其较小。

那么，在分析单桥式变流器时采取如下的假设：

1）电动势是完全对称的正弦波；

2）整流电流中无波动（I_d=常数）；

3）以理想阀替代实际阀；

4）不考虑等值电路中的电阻；

5）设备的自身电容被忽略；

6）变压器的励磁电流等于0。