单向连接状态下带并联电抗器输电线路的优化方案

下面分析在中间点上带并联电抗器的输电线路的单向连接状态。此时，假设线路首端的电压U₁是不变的。

当I₂=0时，线路断开侧的电压U₂由下列表达式确定

其中 А_э——带并联电抗器线路的等值二端口网络系数。

在这种情况下，等值二端口网络系数的确定方法已经在第4章中给出了。当电抗器连接到线路的中间点上时，在此给出这些系数的最终表达式：

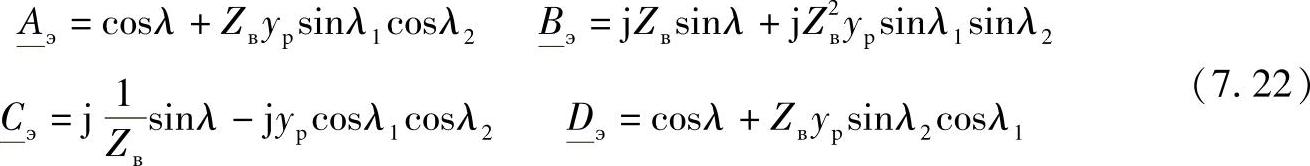
其中 λ——整个线路的波长，λ=λ₁+λ₂。

此时，线路单向连接状态下的输入阻抗被确定为

下面分析当电抗器连接在线路不同点上的情况，假设U₁=常数。

电抗器连接到线路首端（见图7.7a），λ₁=0；λ₂=λ。

此时等值二端口网络的系数等于

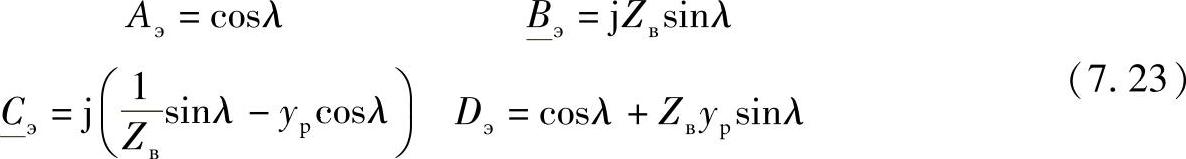
当电抗器连接到线路首端时，电压和无功功率分布的曲线如图7.7b所示。

显然，此时电抗器对线路末端的电压及电压的沿线分布没有产生任何影响；同样，对线路首端的无功功率及无功功率的分布也不产生影响。换句话说，此时状态参数与无电抗器时的状态参数是相同的，电抗器只是作为吸收线路流出无功功率的手段。

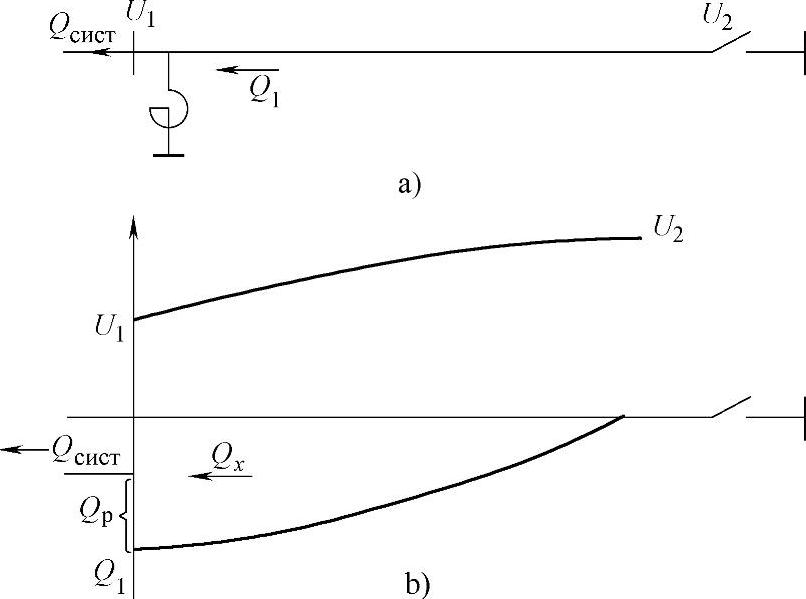
图7.7 电抗器连接到线路首端

a）线路示意图 b）电压和无功功率沿线分布

由线路流向系统的无功功率等于

Q_сист=Q₁^-Qр由式（7.22），此时可以得到线路的输入阻抗

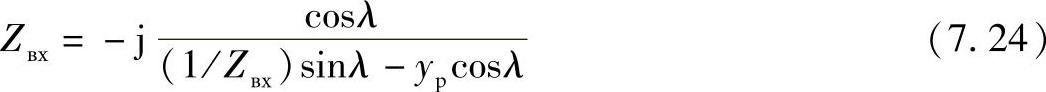
由此可以看出，带有连接到其首端电抗器的线路的输入阻抗，比无补偿线路的大。这对于防止同步状态下的发电机自励磁是有意义的，后文中将进行分析。

电抗器连接到线路的末端（图7.8a），λ₁=λ；λ₂=0。

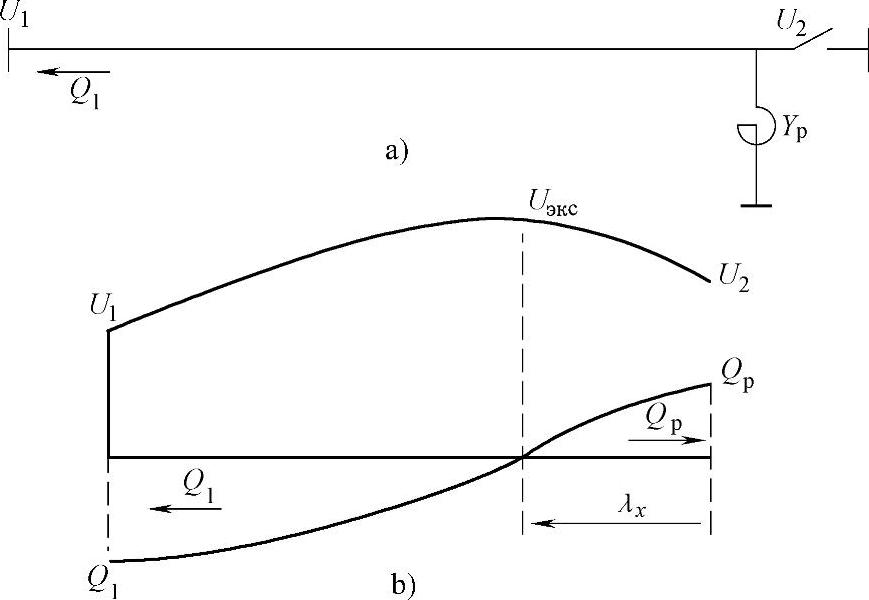
图7.8 电抗器连接到线路末端

a）线路示意图 b）电压和无功功率的沿线分布

等值二端口网络的系数等于：

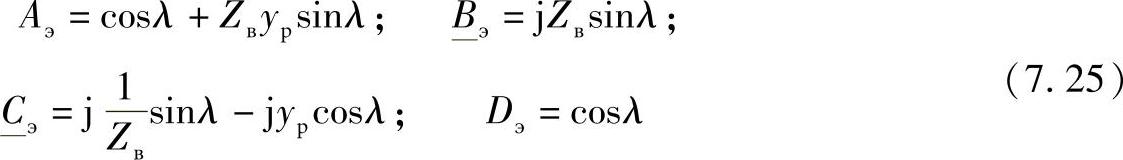
在单向连接状态时，线路末端的电压等于

从这个表达式中可以看出，因为在此时А_э＞А₀，线路末端的电压将小于线路首端连接电抗器的情况。

式（7.26）可用于选择电抗器的导纳，以保证此时的电压期望值U_{2 жел}。如果采取U₂=U_{2 жел}可以得到：

由上式可见，只有当U₁/U_2жел＞cosλ时（即当线路长度超过400km时），才有解存在。

末端带有电抗器时的电压沿线分布由表达式（3.43）确定。当P=0时（线路末段的开关断开），这个表达式具有如下形式：

U_x=U₂（cosλ_x+Q_∗2 sinλ_x） （7.28）

其中 U₂——线路末端电压的实际值。

此时，Q_∗2是导纳为y_р的电抗器所消耗的功率，当电压为U₂以及按照U₂确定基准功率时：

此时，沿线电压和无功功率分布如图7.8b所示。

通常情况下，线路中间点上的电压比两端的电压高。存在位于距离线路末端λх的某电压极值U_экст，在一些情况下这个点上的电压可能超过允许值。为了得到此点上的电压值，必须确定极值点的坐标。为此求导数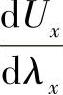，并令其等于0：

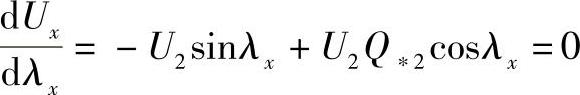
由此，电压极值点的位置被确定为

λ_экст=arctanQ_∗2或者考虑式（7.29）

λ_экст=arctan（y_рZ_в） （7.30）

注意到，电压极值点的位置不依赖于线路的长度，而只是取决于电抗器的导纳和线路的波阻抗。因此，当线路的长度减小且电抗器导纳不变时，极值点将向线路首端移动。此时该点的电压也降低。进一步地，按照式（7.30）确定距离λ_экст后，根据式（7.28）得到极值点的电压，并且按照电晕和无线电干扰进行校验。

考虑到极值点是无功潮流的分界点，流向电抗器的线路无功功率可以确定为

同时，从线路流到受端系统的无功功率等于

必要时，需要补偿此无功功率，通常采取在线路首端安装电抗器的措施，其功率由系统母线上的线路连接点无功功率平衡条件来确定：

Q_р=Q₁-Q_{систдоп} （7.33）

其中 Q_{систдоп}——可能被供电系统采取的无功功率允许值。

此时，线路的输入阻抗可以由式（7.25）确定：

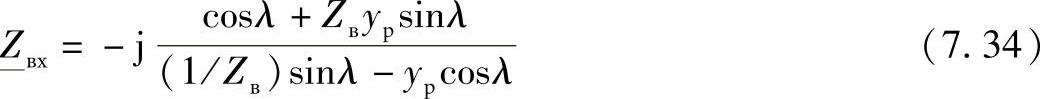
从中可以看出，这个表达式的分子比无电抗器线路和首端带有电抗器线路表达式的分子大，而分母较小。由此可以得到，此时线路的输入阻抗将比上述两种情况大。就是说，电抗器连接到线路末端是更有效的。

电抗器连接到线路的某中间点上（见图7.9a）。此时，决定线路末端电压的等值二端口网络参数А_э被方程组（7.22）给定。而此时线路末端的电压等于

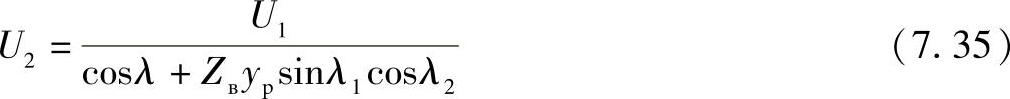
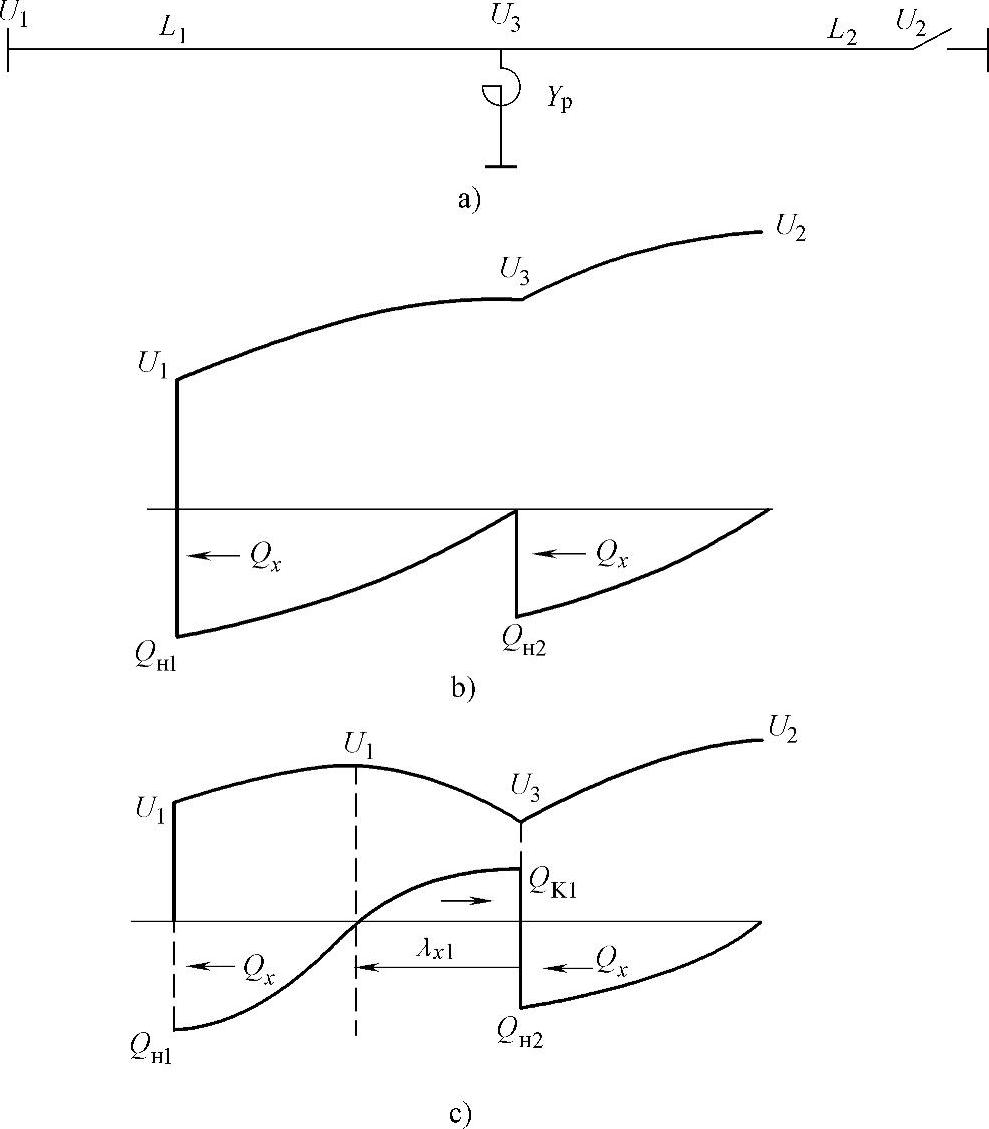
图7.9 电抗器连接到线路的中间点上

a）线路示意图 b）当Q_р=Q_н2时，沿线电压和无功功率分布 c）当Q_р＞Q_н2时，沿线电压和无功功率分布

由此，当给定电压U₁和U_{2 жел}时，可以得到电抗器的导纳：

不难看出，与式（7.27）所示的条件相同，即线路长度超过400km时，才有解存在。

沿线电压和无功功率的分布，由连接点和电抗器的导纳决定。根据这些关系，线路的状态将发生改变，在此分析三种情况。

1）假设电抗器的功率准确地与线路第二分段的充电功率在电抗器的连接点上相等Q_р=Q_н2（同时假设电抗器的功率调节是连续的）。此时，线路正好被分为两个相互独立的部分（见图7.9b）。第一分段的无功功率在电抗器的连接点上等于0，随后无功功率像终端无电抗器、长度为L₁的线路那样变化，这使得可以单独地分析每一分段。第二分段首端的无功功率Q_н2和电抗器功率Q_р由下列表达式确定：(www.xing528.com)

对比上述两个式子，得到

电抗器连接点的电压为

考虑到，分析线路第一分段时与第二分段的情况无关，电压U₃同样可以确定为：

从线路流向其首端的无功功率由第一分段的长度确定

2）假设电抗器的功率比线路第二分段的充电功率大（见图7.9c）。在此，线路第二分段的充电功率和第一分段的部分充电功率都流向电抗器。长度为L₂的线路第二分段，其末端无负载，从而与终端无电抗器线路的特性是相同的。

电抗器连接点的电压U₃

U₃=U₂ cosλ₂（7.42）

第二分段电压分布按照下式确定：

流向电抗器的线路第二分段首端的无功功率

此时，第一分段电压的分布是距离电抗器连接点λх1处有电压极值U₄，并且U₄>U₃。

极值点的电压U₄及其位置可以通过下列关系得到：考虑到这个点同时也是线路第一分段潮流分界点，则

联立求解上述方程，得到

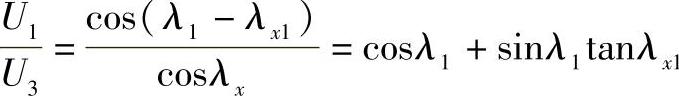
由此

第一分段首端的无功功率等于

流向电抗器的第一分段末端的无功功率由下式来确定：

电抗器吸收的无功功率等于

Q_р=U²₃y_р=Q_к1+Q_н2

或者

3）假设电抗器的功率比线路第二分段的充电功率小。此时，线路第二分段的充电功率部分被电抗器吸收，另一部分流向线路的第一分段。因此，第一分段末端的无功功率等于

Q_к1=Q_н2-Q_р （7.50）

其中

反过来，电压U₃可以由下式确定：

第一分段末段的无功功率可以作为两部分的和：第一分段固有的充电功率和第二分段流出的功率

沿第一和第二分段的电压分布由下列方程确定：

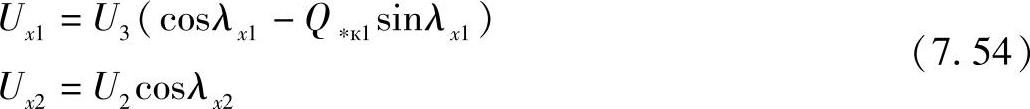
其中，Q_∗к1=Q_к1Z_в/U²₃。

应该注意的是，当前坐标l_х1和l_х2是从相应的第一和第二分段末端向线路首端方向开始计量的。

中间点上有电抗器线路的输入阻抗由下式确定：

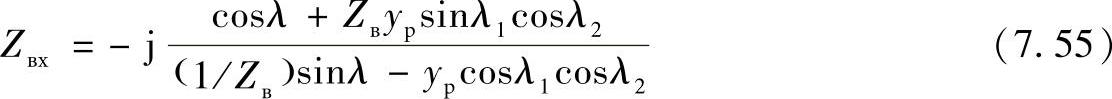
从中可以看出，此时的输入阻抗同样比无补偿线路的输入阻抗大。

电抗器连接到线路两端（见图7.10a）。此时，线路可以表示为如下形式的等值二端口网络模型：

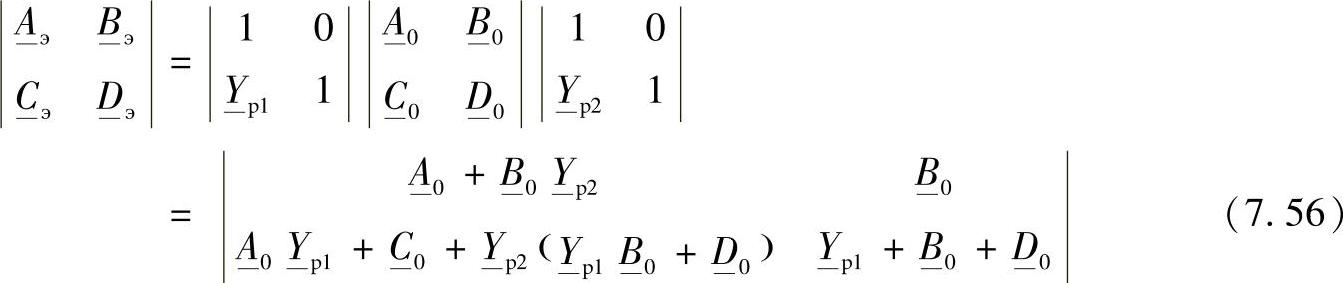
当电抗器的导纳相等时（Y_р1=Y_р2=–j_yр），等值二端口网络的系数为

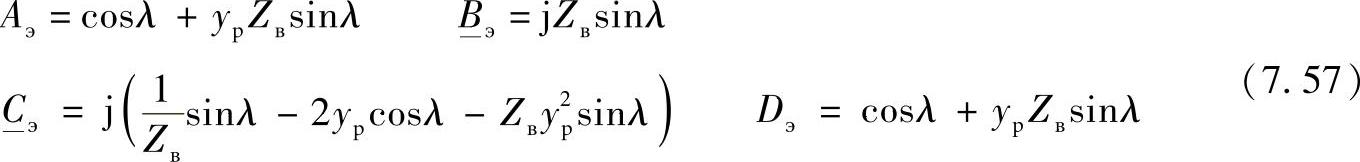
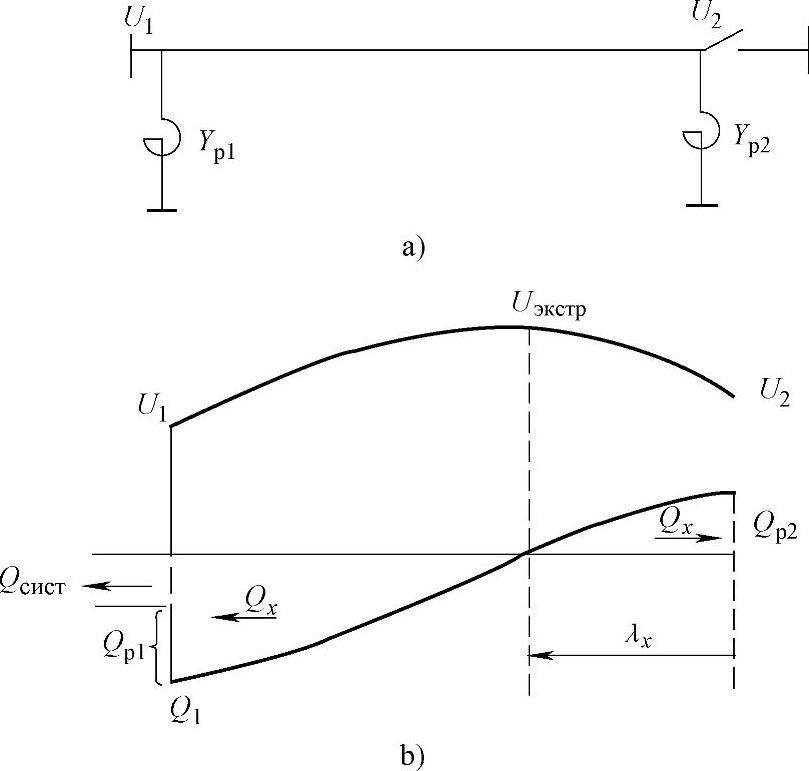
图7.10 带有两个连接到其两端的电抗器线路

a）线路示意图 b）电压和无功功率的沿线分布

比较（7.25）（单个电抗器连接到线路末端的情况）和（7.57）中的常数Aэ，可以看出，它们是相等的。因此，这两种情况下的电压同样是相等的，电压和无功功率分布也相同（图7.10b）。

连接到线路首端的电抗器，对其状态参数不产生任何的影响。因为连接点的电压U₁=常数，此状态下的主要问题在于吸收线路流出的无功功率。同时，如果在计算中考虑供电系统阻抗（U₁≠常数），那么连接到线路首端的电抗器除了吸收线路流出的无功功率之外，也降低其末端的电压。此时，等值二端口网络系数表达式的形式将区别于（7.56）和（7.57）。通常在长线路上，电抗器是从两侧连接的。这是为了补偿其充电功率，同样也是为了在切断线路两端任何一侧的开关时使得状态参数符合标准。

在单向连接状态下，两个电抗器相同时线路的输入阻抗为：

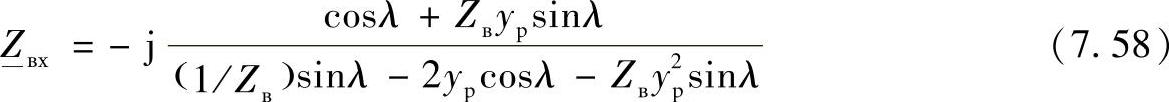
与无补偿线路的输入阻抗和只是一个电抗器连接的线路输入阻抗相比较大。

在单向连接状态下，电抗器对线路输入阻抗的影响可以通过下面的例子来说明。

分析长度为500km、波阻抗Z_B=290Ω的500kV线路，电抗器的导纳y_p等于6.53×10^-4 S（525kV系列不可控电抗器）。

线路的输入阻抗（Z_вх/Ω）随电抗器连接点变化为：

无电抗器线路 -j502

线路首端有电抗器线路 -j744.5

线路末端有电抗器线路 -j829

线路首端和末端都有电抗器的线路 -j1467那么，在单向连接状态下，电抗器从线路的两个方向连接使得其输入阻抗大约增加了三倍。