单向连接状态下的7.2无补偿输电线路

下面分析长度为L、单方向连接到电压不变母线上、另一个方向被断开的线路（见图7.1a）。

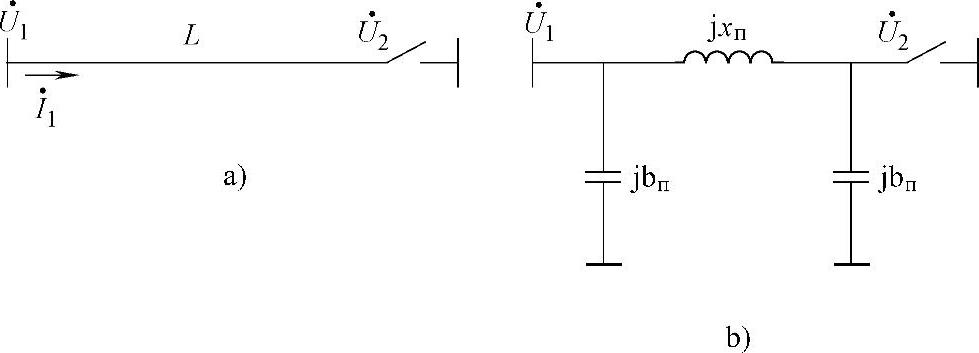
图7.1 单向连接的无补偿线路

a）线路示意图 b）末端开关断开情况下的理想线路П-型等值电路

当电流I·₂=0时，由长线路方程（3.13）、（3.25）可以得到实际和理想线路末端的电压：

在这一章中，为了简化计算，下面将使用理想线路的方程。

因为在式（7.1）中，分数的分母总是小于1，线路断开侧的电压将比首端的电压高。这个结论同样可以从等值电路中得到（见图7.1b）。其中，等值电路纵向支路的电抗jxП与横向支路的电纳1/jbП是并联的。

由式（3.24），当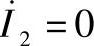时，理想线路距离其末端距离为lх中间点上的电压将被确定为：U_x=U_{2 cos}λ_x

或者计及式（7.1）有

由方程（3.24），理想线路中间点上的电流当I₂=0时等于

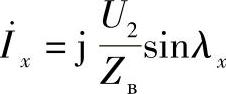
可以得到线路中间点上的功率

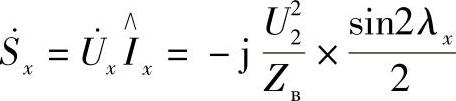
或者计及式（7.1）有

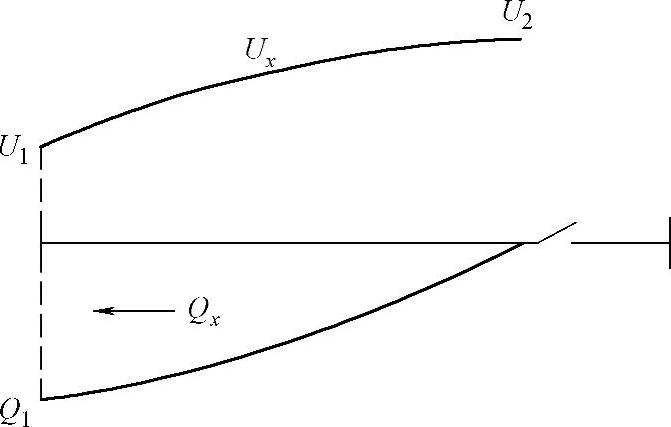
图7.2 沿线电压U_x和无功功率 Q_x分布的曲线图

电压和无功功率分布曲线如图7.2所示。

当λ_х=λ时，线路首端的电流和功率分别为：

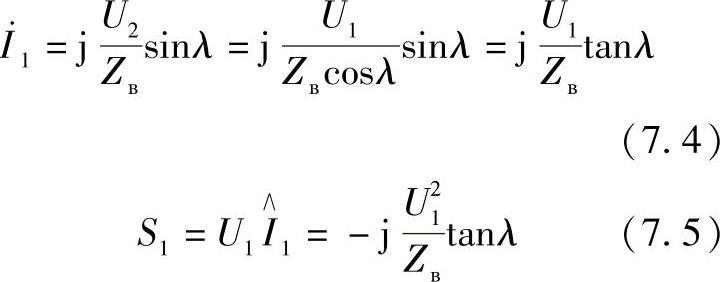
此无功功率由线路流向线路所连接的系统或者是发电厂的发电机母线。

由方程（7.1）和（7.5）可以看出，在此状态下，当线路长度增加时，断开侧的电压和线路流出的无功功率升高。当线路长度为1500km（1/4波长）时，理想线路的电压和无功功率等于无穷大；而相同长度的实际线路因为电晕的影响断开侧的电压是有限的，但是此时其电压仍将是很高的，对线路和设备的绝缘是很危险的。实际线路首端的功率同样很高，除此之外，由于导体发热和电晕损耗，其中还出现了有功分量。

对于不同长度理想线路末端电压与其长度的关系，以及沿线电压分布如图7.3所示。

此状态下理想线路的输入阻抗为

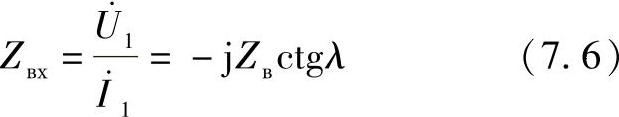
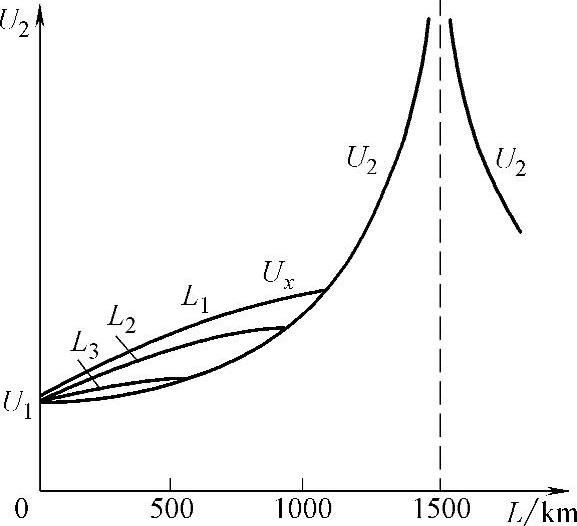
图7.3 线路断开侧电压U_x分布与 长度的关系（L₁>L₂>L₃）

从方程（7.6）中可以看出，此状态下长度小于1500km线路的输入阻抗是容性的，并随着长度的增加而减小。当线路的长度为1500km（λ=p/2）时，线路的输入阻抗等于0。可以发现，此时线路末端的电压等于无穷大，也就是说，线路工作在谐振状态下。

为了解释这个现象，来分析单向连接状态理想线路的等值电路（见图7.1b）。此状态下纵向支路的电抗是串联的，等于

x_п=jZ_в sinλ

并且等值电路横向支路的电抗

x_С=-jZ_в ctg（λ/2）

当线路长度为1500km时，这两个阻抗（感性和容性的）的模值是相等的，而它们的总阻抗等于0，这就解释了电压谐振的现象。这样的论述包含着一些近似，但是足够准确地反映了线路上所发生过程的本质。

就像已经指出的那样，线路断开侧的电压在本状态下比其首端的电压大，符合按照超高压变电站设备（开关、电流互感器、电抗器等）绝缘工作条件确定的技术运行导则。所允许的短时间电压升高，不超过额定值的10%。其中，电压升高的时间不应该超过20min。

那么，线路断开侧短时允许的电压U_{кр доп}等于

U_{кр доп}=1.1U_ном （7.7）

令U₂=U_{кр доп}可以确定线路的临界长度，当超过此临界长度时，电压U₂>1.1U_ном。这个长度大概为400km，可能存在不大的偏差，可以通过电磁波的相应分布系数β_o的偏差来解释。

对于400km长的线路，线路断开侧的电压等于：

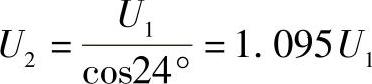
即实际上是在允许电压的边界上。

当线路长度增加时，必须采取降低其末端电压的措施。

由线路上流出的无功功率可能非常大。那么，对于长度为400km的500kV线路，当波阻抗的平均值Z_в=290Ω时，无功功率等于：

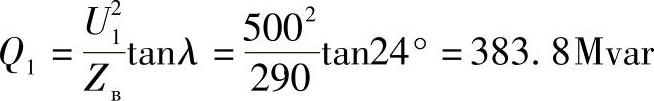
如此大的无功功率要求采取补偿的措施。

下面分析当线路所连接的母线不是电压不变母线，即当连接到此母线的供电系统阻抗不等于0时，这可能存在如下的情形。

1）被分析的线路连接到发电厂母线上，发电机装设有比例或者强励调节器，维持E_q′=常数或者Uг=常数，线路示意图如图7.4a所示。

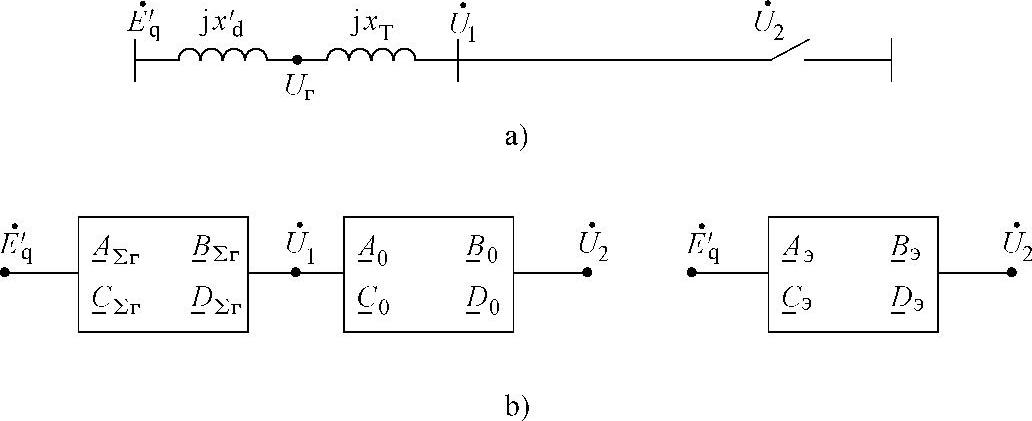
图7.4 线路经过阻抗连接到电压不变母线上

a）经过变压器阻抗连接到装设有APB的发电机母线上 b）二端口网络等值电路

在这种情况下，具有比例调节器的供电系统等值阻抗等于

x_сист=x_d′+x_т具有强励调节器的供电系统等值阻抗等于

x_сист=x_т

x_d′和x_т根据并列运行发电机的数量和发电厂的接线确定。

2）电压不变母线是供电系统的中压母线，而本线路最终是通过自耦变压器与高压母线连接。此时x_сист=x_АТ，x_АТ通过并联工作的自耦变压器来确定。

3）本变电站的高压母线与由等值阻抗x_сист表示的、接线略微复杂的系统电压不变母线相联系。

二端口网络表示的线路如图7.4b所示。

当考虑送端系统阻抗时，借助于整个线路的等值二端口网络模型，在给定发电机或者系统不变电压的情况下可以得到线路断开侧的电压。这个二端口网络的参数矩阵有如下形式

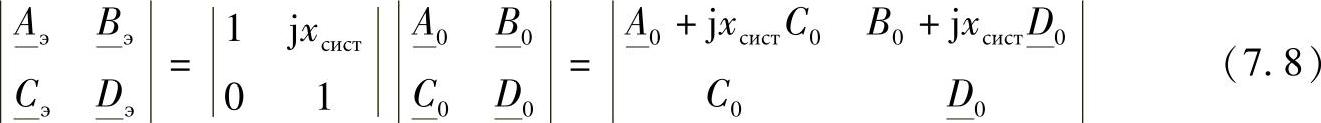
其中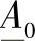、、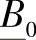、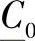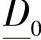——线路的等值二端口网络系数；

х_сист——供电系统等值阻抗（在个别情况下是发电机阻抗x_d′和升压变压器的阻抗）。(www.xing528.com)

此时等值二端口网络的系数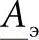等于

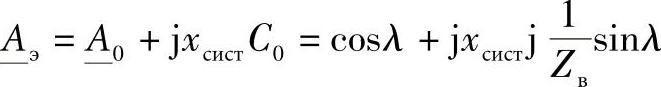
或者

线路断开侧的电压等于

其中 U_сист——被连接到与线路同一电压等级的系统电压。

就像从式（7.9）中可以得到的那样，А_э＜А₀。由此，此时线路断开侧的电压将比由电压不变母线供电时的线路大。

在确定系统和线路参数之间关系时，А_э可能等于0，从而导致断开侧的电压升高到无穷大，产生了电压谐振。

发生电压谐振的线路长度，可以由式（7.9）得到。令А_э=0，变换后得到

由此

L_рез=λ_рез/β₀

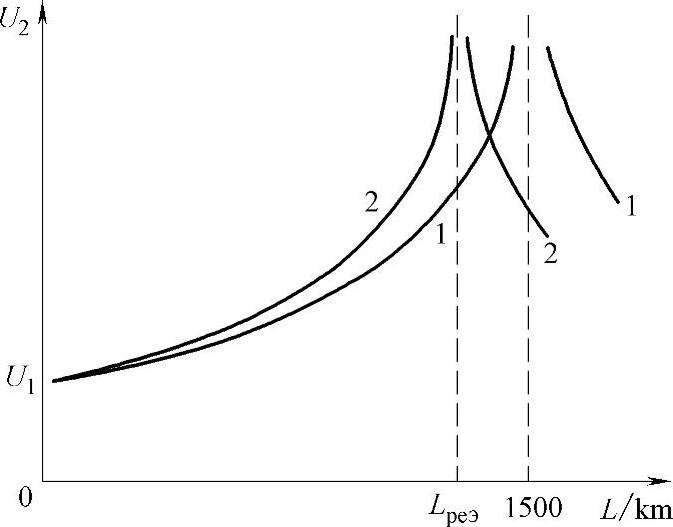
图7.5 系统阻抗对电压U₂的影响 1—不考虑阻抗 2—考虑系统阻抗

断开侧电压变化与线路长度的关系，以及此时的电压分布如图7.5所示。从中可以看出，当线路长度较短时，发生谐振。与不考虑系统阻抗的情况相比，断开侧的电压急剧升高。

在考虑系统阻抗时，线路首端的电压等于

U₁=U₂ cosλ （7.11）

其中，U₂由表达式（7.10）确定。

线路首端的无功功率按照式（7.5）计算，其中U₁由表达式（7.11）确定。

此时系统母线上的无功功率等于

Q_сист=Q₁-ΔQ （7.12）

其中 ΔQ——系统等值阻抗上的无功损耗。

沿线电压分布按照式（7.2）确定，其中U₁可以由式（7.11）得到。

将由式（7.9）得到的Аэ和由（7.10）得到U₂代入到方程（7.11），得到：

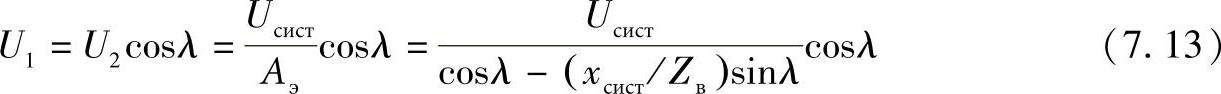
如果比较上述两种情况（线路连接到电压不变母线和线路经过电抗连接到电压不变母线上），可以从得到的方程中看出，线路断开侧的电压U₂、线路首端的电压U₁和线路流出的无功功率Q₁，在第二种情况下较大。这些必须在线路设计时考虑到。

如上所述，输电线路断开侧的电压可能超过允许值。这就要求采取把电压U₂降低到允许界限内的措施，可以有两种方法。

1）为了使线路末端的电压达到期望值U_2жел，要降低线路首端的电压。

2）并联电抗器连接到线路末端或者是距离末端较近的其中间点上。

第一种方法可以在线路计划内投切时使用。当本线路由远方发电厂及其中的部分发电机供电时，可以保证发电机端的电压。如果线路通过自耦变压器连接到系统的电压不变母线上，必须改变自耦变压器的变比（通过有载调压开关）。

在上述情况下，线路首端的电压可以被确定为

U₁=U_2жел cosλ （7.14）其中，电压U_{2 жел}可以取为等于U_{нб раб}或者U_{кр доп}。

代入到式（7.14）的U₁中，线路首端的无功功率由方程（7.5）确定

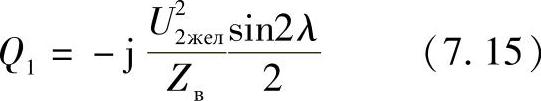
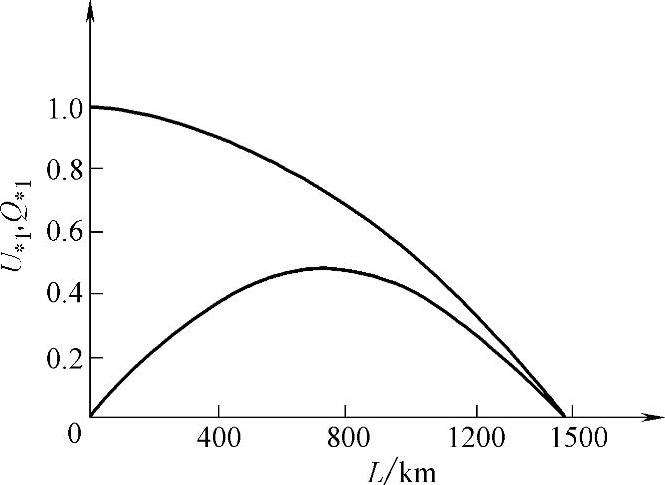
图7.6 在给定断开侧电压时，电压U_*1（1）和无功功率Q_*1（2）与线路长度的关系

当U₂=U_{2 жел}时，U_*1和Q_*1与线路长度的关系如图7.6所示，U_{2 жел}和Р_нат可以取为基准值。

对于发电机—变压器—线路的接线方式（见图7.4a），可以得到由线路流向发电机的无功功率

Q_г=Q₁-ΔQ_т （7.16）

其中

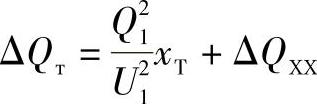
为变压器中的功率损耗。

发电机输出端的电压为

其中k_т——变压器变比。

发电机输出端的电压不能低于0.8U_{г ном}，即按照自动励磁控制系统的工作条件，必须使U_г≥0.8U_гном。

如果线路与系统的电压不变母线通过自耦变压器连接，线路首端电压U₁的降低程度可以由自耦变压器的变比调节范围来决定（有载调压开关的调节范围）。

应该注意，当线路首端电压降低时，Q_г不能被用于按照P-Q曲线校验此状态下发电机的工作能力。因为P-Q曲线是按照发电机的额定电压建立的，此时与U_г＜<U_ном的情况相类似。在此，必须确定发电机的定子电流I_{ст г}，以校验下列条件是否满足

I_стг≤I_{стг ном} （7.18）

换句话说，此状态下发电机的定子电流不应该超过其额定值。

在此，I_{ст г}可以按照下列表达式确定

对于水轮机组，在线路单向连接状态下，所允许的无功功率吸纳可以由下式确定：

其中 x_*d——以标幺值表示的水轮机的纵轴阻抗；

S_гном——水轮机组的额定功率（MVA）。

如果条件（7.18）和（7.20）没有被满足，必须分析在本线路上两个发电机组协同工作、或者使用分流电抗器的可能性。

作为标准化的手段，线路首端电压的降低不可能在所有情况下被推荐使用。尤其是，当本线路断开侧的母线还连接有其他不带负荷的线路，或者这些母线是系统母线、电压只是在不大的范围内变化时，均不允许使用这种方式。

最后，为了使一侧断开线路的状态符合标准，必须使用并联电抗器。