中间变电站补偿装置接线方式简介

在教学实践过程中，通常分析的是带有一个中间变电站的输电线路。

由这个变电站的中压母线对没有自备电源或者是与其他发电机节点无联系的负荷节点供电，此输电线路可能的接线方式如图6.12所示。图6.12a显示了具有相同额定电压的两个分段输电线路示意图。在图6.12b显示了具有不同额定电压分段的输电线路示意图。它们状态的计算方法稍微有些差别。

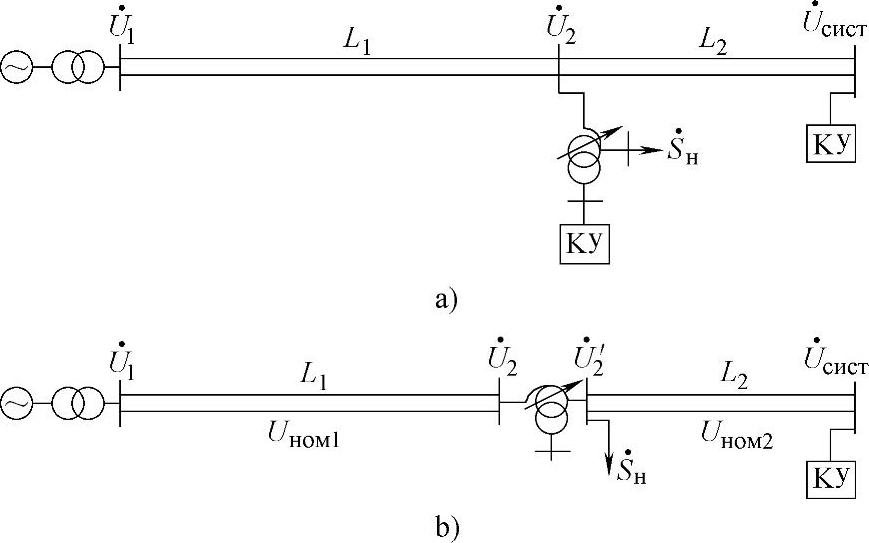
图6.12 具有一个中间变电站的输电线路示意图

a）两个分段额定电压相同 b）分段的额定电压不同

下面分析具有相同额定电压分段的输电线路。

假设，在中间变电站上装设有保证高压母线无功功率平衡的补偿装置（SC、SVC等）。输电线路的两个分段都可以表示为等值电路或者二端口网络的形式，其参数按照第4章所述的方法来确定。此时，应该考虑线路各分段中的回路数和变电站连接的自耦变压器数量。输电线路的等值电路如图6.13所示。送端发电厂和受端系统的接线在此并没有显示，因为它们与在6.2节中分析的相同。重载状态计算的目的是，确定中间变电站补偿装置的功率。给定的原始数据是送端发电厂母线的电压U₁和受端系统母线的电压U_сист，同样还包括输电线路第一分段首端的有功功率Pн1。

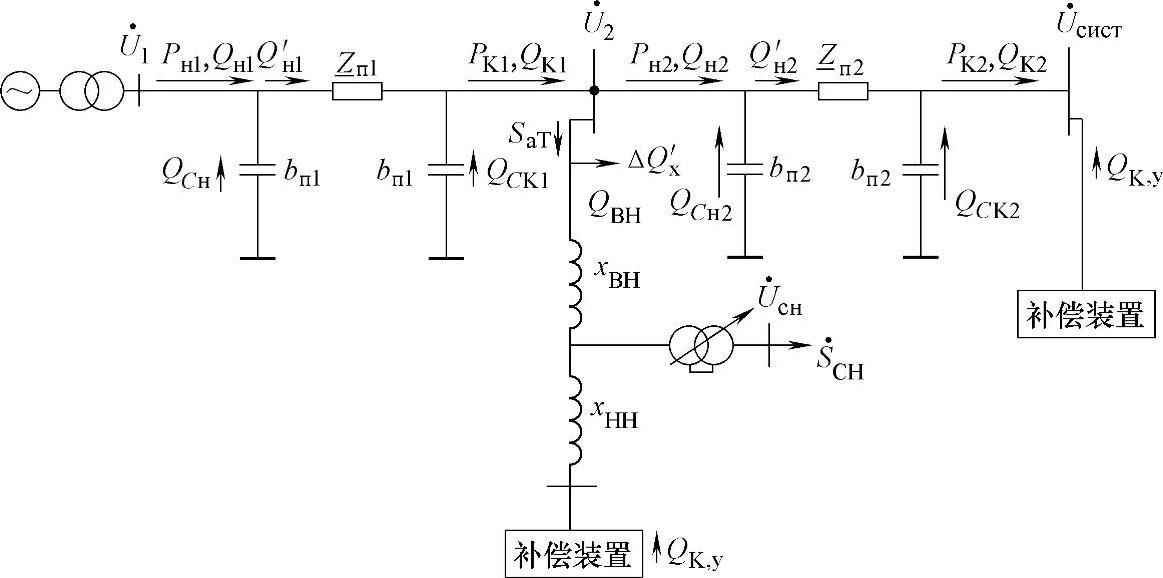
图6.13 具有相同额定电压分段的输电线路等值电路

给定中间变电站母线的电压，并且假设是不变的。下面在给定电压U₁和U₂以及分段首端功率P_н1=P₁的情况下，将输电线路第一分段作为独立线路来分析其状态。然后，按照6.2.3节中所介绍的算法，计算第一分段末端的状态参数P_к1和Q_к1。

从变电站母线有功功率平衡方程中，可以得到第二分段首端的有功功率P_н2：

P_н2=P_к1–P_{н пс} （6.39）

其中 P_к1——线路第一分段末端的有功功率；

P_{н пс}——连接到变电站超高压母线上的负载有功功率。

根据第二分段首端的数据U₂、P_н2和给定的系统电压U_сист，来分析线路第二分段的状态，以确定第二分段首端的无功功率Q_н2以及末端的状态参数P_к2和Q_к2。

根据无功功率平衡方程，确定变电站超高压母线上的所需要的无功功率：

Q_пс==Q_к1–Q_н2 （6.40）

在此，需要注意与变电站相连线路末端无功功率的符号。这些符号取决于线路各分段的长度和其传输的有功功率值（在式（6.40）中，正号与有功功率方向一致）。

进一步地，可以按照已知的方法来确定自耦变压器高压绕组中的无功损耗。根据等值电路零点处的无功功率平衡条件，在计及变电站中压母线负载功率时，计算得到低压绕组末端的功率，并最终得到连接于低压母线上（可能是10kV或者38.5kV母线）的补偿装置功率。超高压自耦变压器低压绕组的功率比其额定功率低很多（通常与额定功率相差30%～50%）。因此，应该校验所需要的补偿装置功率和设在此变电站上的自耦变压器低压绕组功率。如果补偿装置连接在中压母线上，其功率将由这些母线的无功平衡方程确定。

如果使用同步调相机，那么在输电线路的状态计算方法中应该考虑其功率和电动势。在Q_СК≤0.3P_нб时，可以只考虑同步调相机的功率，而不考虑其电动势。当同步调相机的功率较大时，在P_СК≈0时可以作为同步发电机来对待。与励磁控制的类型有关（比例、强励等），在计算中同步调相机可以被表示成输出端电压和功率恒定不变、或者是附加在相应阻抗后面恒定不变的电动势形式。从而，具有单个中间变电站、装设大功率同步调相机的输电线路应该以具有三相同步发电机的电路来分析，使得计算变得复杂很多。

在6.2.4节中，通过计算得到第二分段末端参数P_к2和Q_к2，可以确定输电线路接收端所需要的补偿装置功率。在此，也可以应用该方法。

所分析的输电线路的典型特征是：在电压U₂变化时，第二分段的状态（两端的无功功率，以及中间变电站和系统受端变电站补偿装置功率，有功功率的总损耗等）发生变化。

如果计算不包括选择最优的电压U₂值，那么计算过程到此就结束了，算法如图6.14所示。按照此算法也可以实现输电线路轻载状态下的计算，此时的原始数据是P₁=Pнм，U₁，U₂，U_сист。其中，输电线路所有节点的电压被认为是等于U_ном，或者是出于降低线路充电功率的目的略小于U_ном。

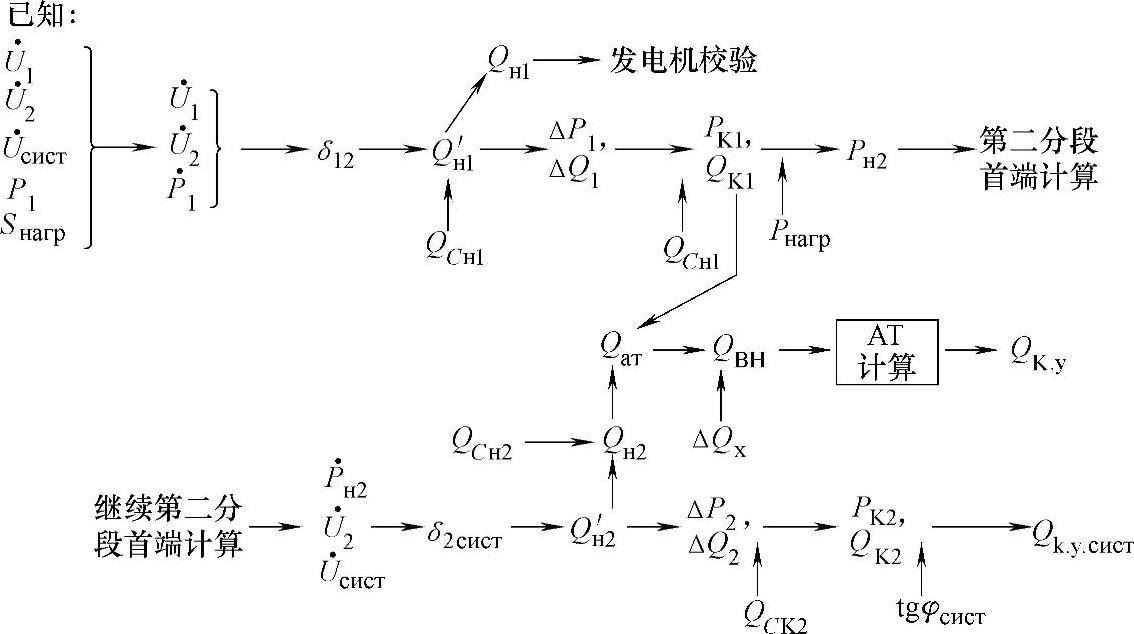
图6.14 具有相同额定电压分段的输电线路状态计算方法

如果需要确定第一分段最优的电压降落，则需要计算一系列的电压U₂值。对于其中的每一个值，要确定第一和第二分段上的有功功率损耗、以及中间变电站和系统受端变电站补偿装置的功率。

在贴现成本计算中，应该考虑线路第一和第二分段的电能总损耗，以及中间变电站和系统受端变电站补偿装置的损耗。

在这两个变电站中的补偿装置总投资以及其运行成本为：(www.xing528.com)

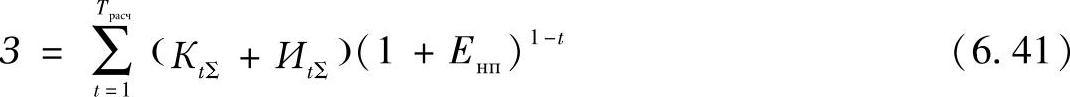
其中 К_tΣ——中间变电站和系统变电站补偿装置的年投资成本，等于：

К_tΣ=К_t1+К_t2

И_tΣ——年运行费用，等于

И_tΣ=（К_t1+К_t2）a+З_Δэ1+З_Δэ2

其中 a——折扣系数；

З_Δэ1，З_Δэ2——线路第一和第二分段的电能损耗成本。

然后，建立К_tΣ、З_ΔэΣ、Q_КУпс、Q_КУсист、З与U₂的关系，以确定U_{2 опт}和相应的功率Q_КУпс以及Q_Кусист。进一步地，确定补偿装置的型号和数量，并且校验其连接到自耦变压器相应绕组上的必要性。

如果线路的部分分段有不同的额定电压，或者它们是通过具有有载调压开关的自耦变压器连接的（图6.12b），那么计算方法与上面所述的稍微有点区别。主要的区别在于，当电压U₂变化时，考虑到有载调压开关的作用，第二分段首端的电压U₂′是不变的。因此，状态参数的变化只是发生在第一分段，并且反映在无功功率平衡计算中。

应用于输电线路等值电路（见图6.15）上，可以写成：

P_н2=P_к1-P_пс （6.42）

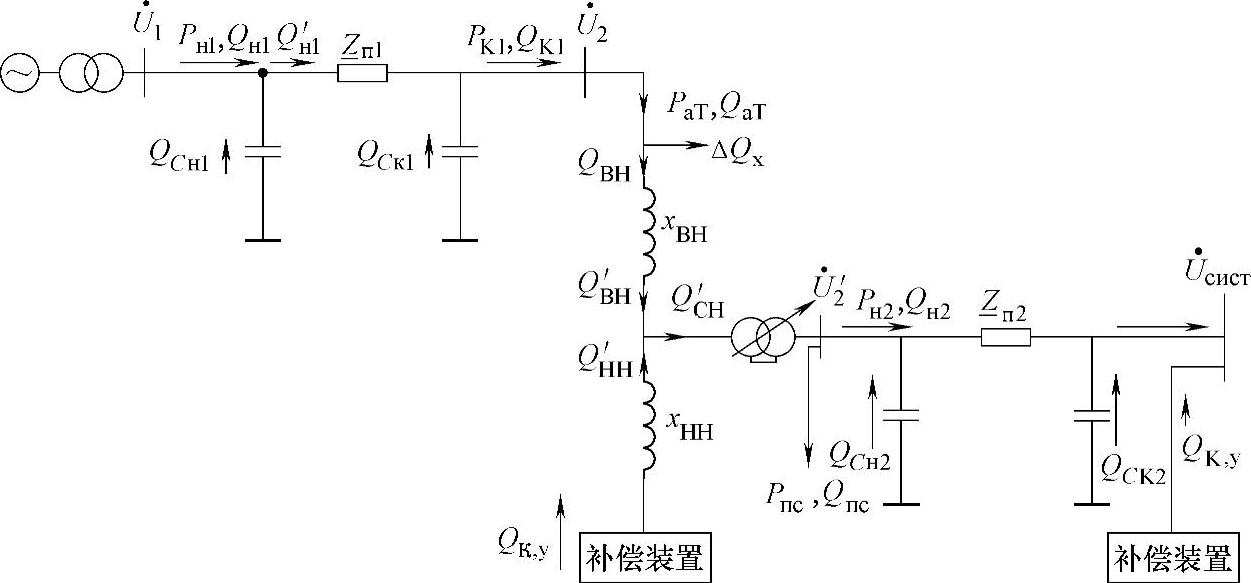
图6.15 具有不同额定电压的输电线路等值电路

进一步地，按照已知的P_н2、U′₂和U_сист表达式，可以得到第二分段首端的无功功率Q_н2。进而确定高压绕组中的无功功率损耗ΔQ_ВН，以及这个绕组末端的无功功率值Q′_ВН：

Q′_ВН=Q_к1-（ΔQ_хх+ΔQ_ВН）

然后等值电路零点处的无功功率平衡方程可以写成：

Q_ВН′+Q′_НН-Q_СН=0（ 6.43）其中

Q_СН=Q_н2+Q_пс

从平衡方程中得到Q_НН′，然后按照得到的Q_НН′确定ΔQ_НН。

连接到自耦变压器第三绕组的补偿装置的功率等于

Q_КУ=Q_НН′+ΔQ_НН

在此情况下，当已知Qк2和Qсист时，可以按照上述算法确定系统受端变电站补偿装置的功率。

当必须确定第一分段的最优电压降落时，电压U₂的变化是在自耦变压器有载调压开关调节的允许范围内，此时电压U₂′是不变的，第二分段的状态参数同样是不变的。电压变化导致的只是第一分段状态参数和中间变电站中补偿装置功率的变化。因此，在确定贴现成本时，应当排除恒定不变的部分。

在轻载状态下，应当使用前面介绍的算法分析输电线路，评价按照最大负荷条件选择的补偿装置过剩无功功率的可能性。如果补偿装置不足以吸收过剩无功功率，在所采取的变电站电压下、为了保证无功功率平衡，不需要这么多过剩的无功功率，则必须使用连接于线路末端的并联电抗器。如果电抗器直接连接到变电站母线上，需要进行额外的论证。电抗器的功率是按照输电线路每个节点的无功平衡条件来确定的，包括发电厂、中间变电站和系统受端变电站的点。

受端系统变电站补偿装置的选择应当按照6.2.4节中所述的方法进行。

降低线路充电功率的方法之一是：降低输电线路和系统母线上的电压，使其比额定电压低3%～5%。尽管是在轻载状态下，输电线路和系统母线上的电压降低也不能对与此输电线路相连的系统静态和动态稳定性产生影响。

利用发电厂中的发电机也可以降低汇集在线路上的无功功率。当输电线路是发电厂和系统之间的联络线时，减少发电厂所发出的无功功率，可以降低线路电压降。显然，此时必须检验线路接收端——中间变电站和受端系统吸纳额外无功功率的可能性。