【摘要】:因为线路的功率圆反映了线路首端和末端的状态参数,可以合理地使用等值二端口网络模型来表示带补偿线路。在计及所有连接于线路上的集中参数元件情况下,方程(5.2)使用了等值二端口网络参数,方程的第一项是圆心坐标g,第二项是半径——向量r,r的位置随着角度d的变化而改变。
因为线路的功率圆反映了线路首端和末端的状态参数,可以合理地使用等值二端口网络模型来表示带补偿线路。此二端口网络的坐标是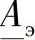 、
、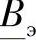 、
、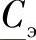 、
、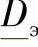 ,其中计及了所有线路所连接的补偿装置。
,其中计及了所有线路所连接的补偿装置。
补偿线路首端的电压和电流与线路末端参数的关系可以表示为:
由式(5.1)的第一个方程可以得到:
代入式(5.1)的第二个方程中,并计及:
简单变换后得到:
线路首端的复功率由下列方程确定:
将电流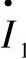 的共轭复数代入到上述方程中,有:
的共轭复数代入到上述方程中,有:
其中,电压相量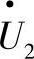 与横坐标轴一致(
与横坐标轴一致(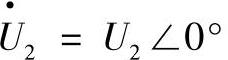 ),则
),则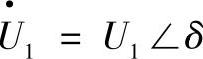 ,并最终得到:(https://www.xing528.com)
,并最终得到:(https://www.xing528.com)
这个方程就是补偿线路首端的功率圆方程,如果二端口网络系数反映的只是线路本身参数的话,它同样是无补偿线路的功率圆方程。
在计及所有连接于线路上的集中参数元件情况下,方程(5.2)使用了等值二端口网络参数,方程的第一项是圆心坐标g,第二项是半径——向量r,r的位置随着角度d的变化而改变。圆心的位置和向量半径的值是线路补偿元件设置地点和参数的函数。
也可以得到补偿线路末端功率圆方程。
解方程(5.1),得到相应的线路末端电压和电流:
代入到第二个方程中,经过变换,可以从(5.3)的第一个方程中得到电流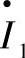 。与上述过程相类似,可以得到:
。与上述过程相类似,可以得到:
修正后,如上所述,电压向量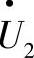 与横坐标轴一致,得到
与横坐标轴一致,得到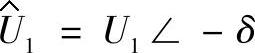 。最终有:
。最终有:
这个方程是补偿线路末端功率圆方程。在此,方程的第一项同样决定了圆心的位置,第二项是向量半径。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




