在计算复杂输电线路状态时可以使用等值的二端口模型,装设带有中间功率输出的各种补偿装置的线路都属于复杂输电线路,与П-型或者Т-型等值电路相比,符值二端口模型具有一定的优势。这些优势更多地体现在确定输电线路的自阻抗、互阻抗和输入阻抗时,不需要经过电路变换或者使用其他的复杂而繁琐的计算方法。
此模型不仅可以得到等值二端口网络输入和输出端参数之间的关系,同样可以确定输电线路任何一个中间点上的状态参数。作为等值模型的一部分,此中间点是子二端口网络输入和输出的端点。
在输入端参数给定时,二端口网络输出端的状态参数可以通过联立求解方程(4.1)得到:
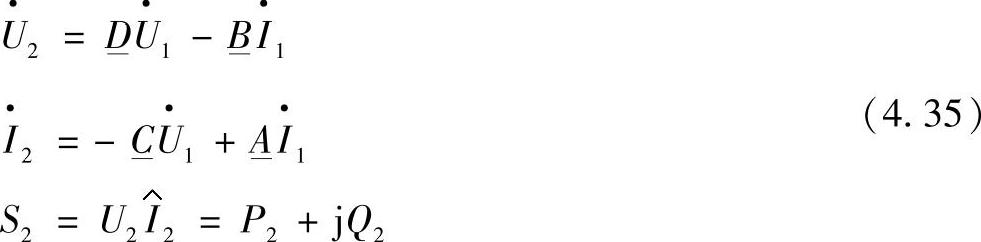
在输入端参数给定时,也可以得到输电线路任何一点的状态参数。
在输电线路的等值电路中,子二端口网络可以被串联,也可以被并联。在串联时,等值二端口网络的参数矩阵可以通过各个子二端口网络的参数矩阵累乘得到,此时计算产生中间矩阵,代表了输电线路其他一些点上的状态参数。
在双回输电线路情况下,必须使用并联二端口模型。尤其是在分析不均匀网络时,输电线路各个回路不相同、较低电压等级线路被并联于此线路,以及其他的一些情况下,也必须使用并联二端口网络模型。
下面分析两个不同的二端口网络并联,系数A、B、C、D是不同的(见图4.7)。
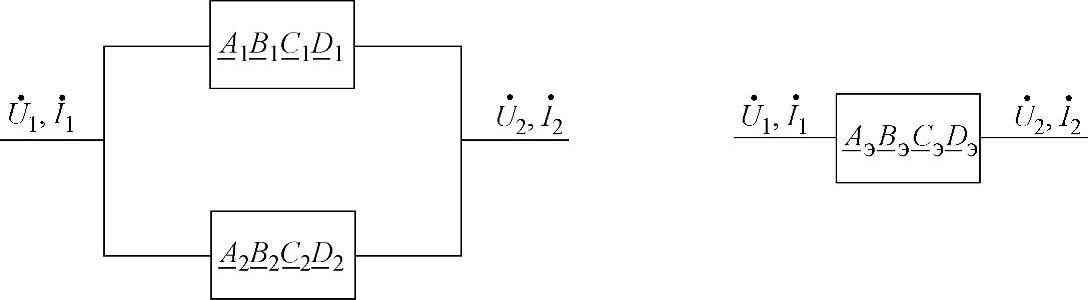
图4.7 二端口网络并联
由电工理论基础知识可以得到,等值二端口网络的自导纳和互导纳与子二端口网络导纳间有如下关系:
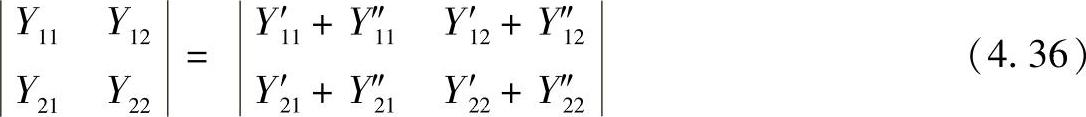
式中,Y11,Y12,Y22,Y21——子二端口网络的自导纳和互导纳(上标′表示第一个二端口
网络,上标″表示第二个二端口网络)。
通过二端口网络参数表示的导纳为:
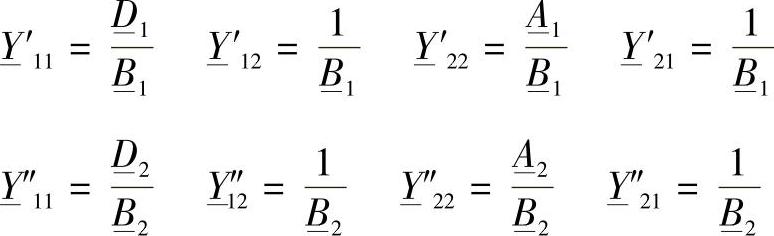
将这些导纳代入到原始方程(4.36)中,变换后得到:
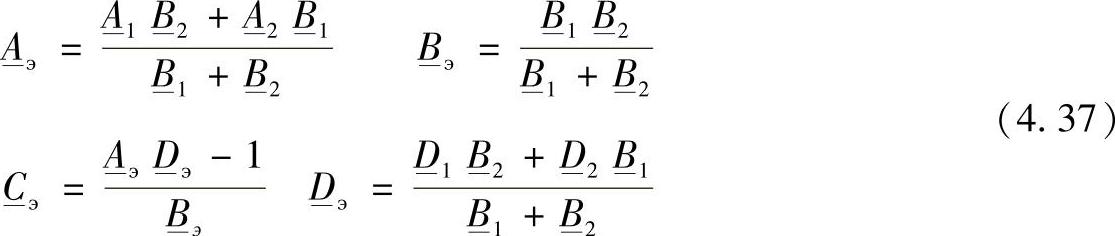
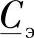 同样可以通过每个二端口网络参数得到:
同样可以通过每个二端口网络参数得到:
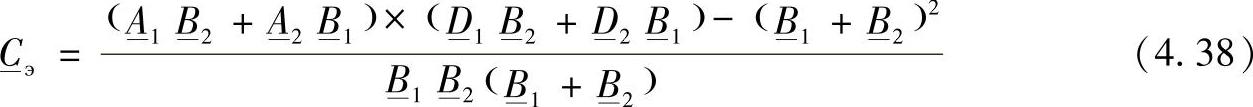
当并联的二端口网络相同时(一条线路具有两个相同的回路、两个相同的并联工作变压器或者自耦变压器),等值二端口网络的参数将是相等的:
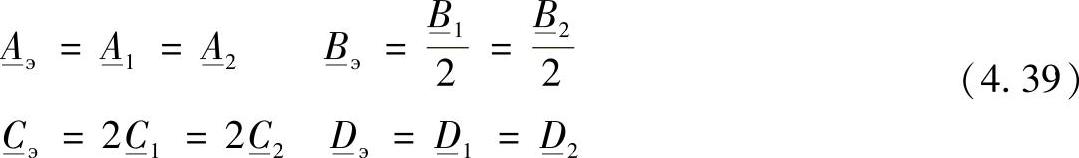
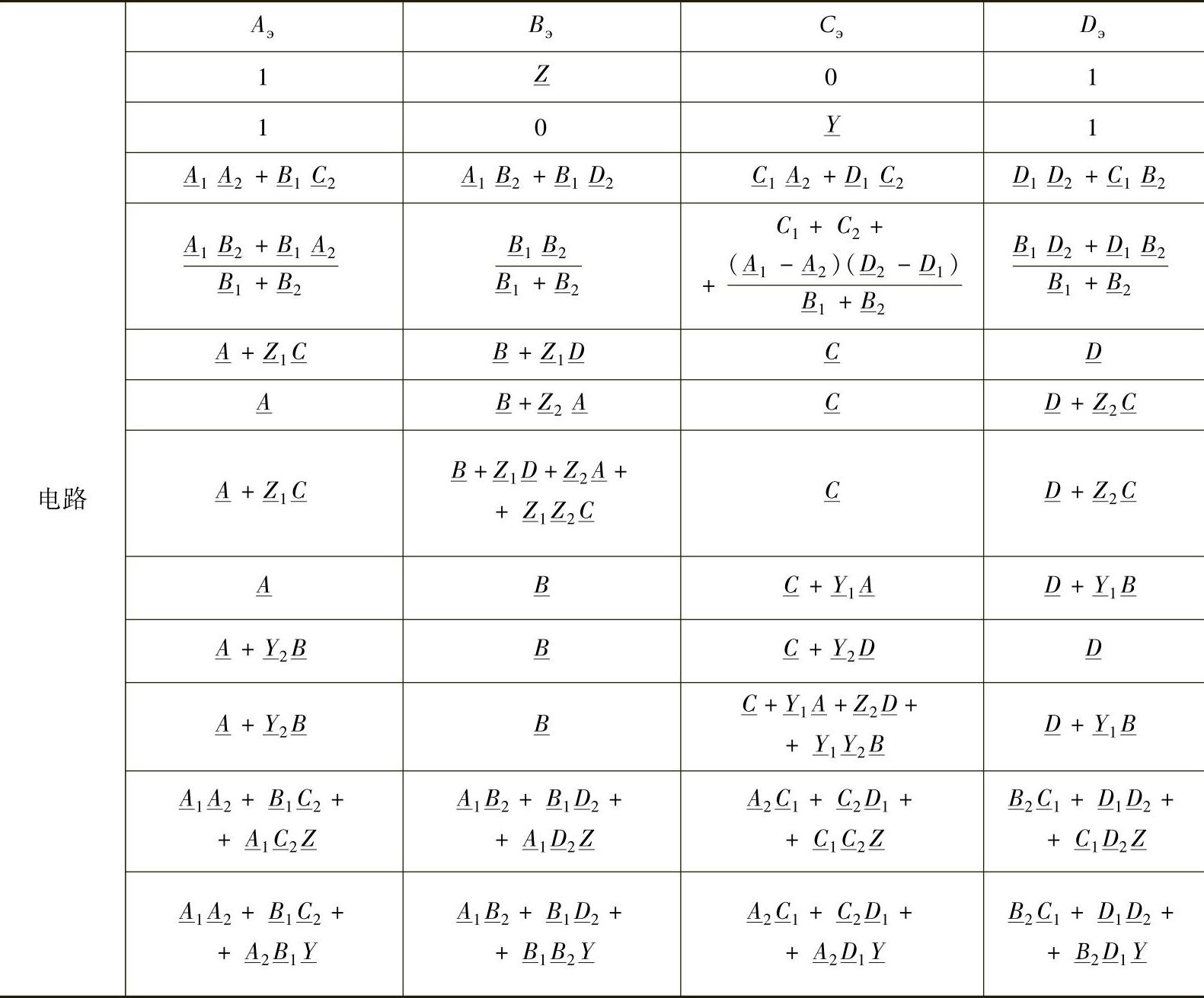
输电线路其他元件的各种二端口网络连接方案如表4.2所示。
下面分析等值二端口网络模型在最典型情况下的应用。
发电机—变压器—线路示意图如图4.8所示。整个输电线路的等值二端口网络参数矩阵通过其中的子二端口网络参数矩阵的乘积确定:
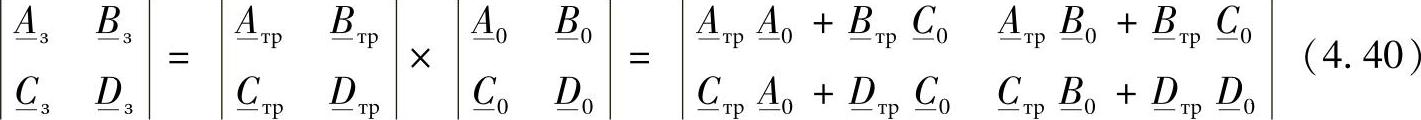
在此和以后的下标符号“0”表示“自然”线路的等值二端口网络参数,即没有中间变电站以及没有任何集中参数装置的线路。
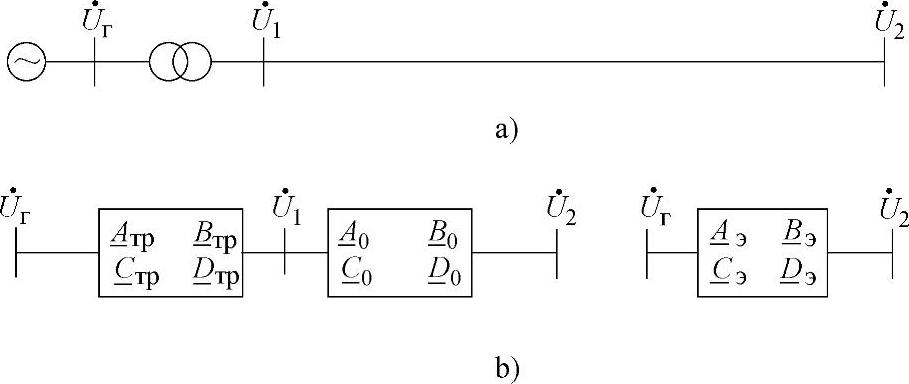
图4.8 发电机—变压器—线路示意图(a)以及等值二端口网络表示(b)
如果变压器只是以泄漏阻抗来表示,那么等值的二端口网络参数被确定为:
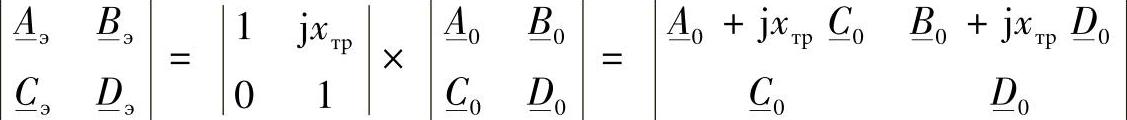
表4.2 等值电路参数之间的关系
对于理想线路,考虑式(4.3),有:
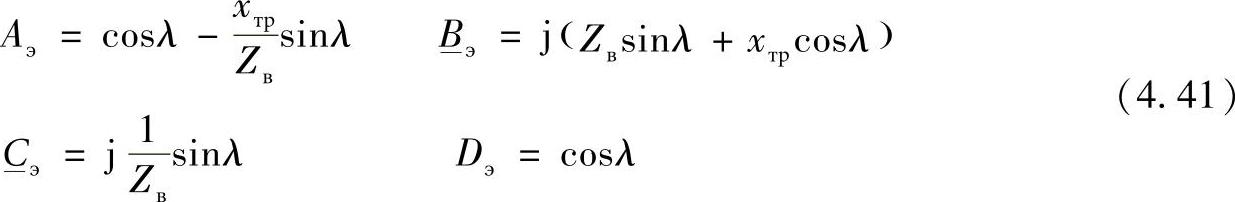
在发电机状态参数(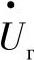 ,
,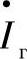 )给定的情况下,线路首端的状态参数以如下方式确定:
)给定的情况下,线路首端的状态参数以如下方式确定:
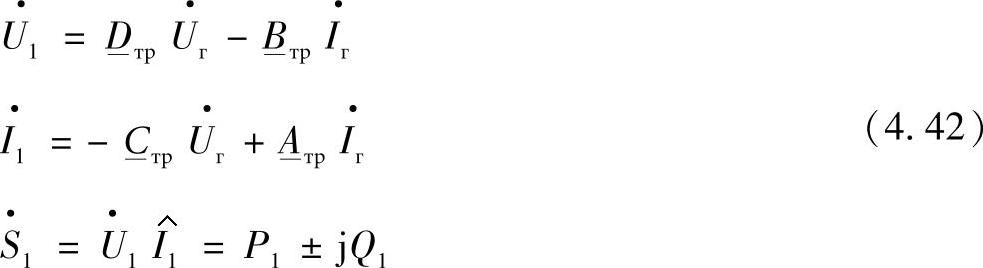
或者,计及Aтр=Dтр=1,Bтр=jxтр,Cтр=0,可以得到:
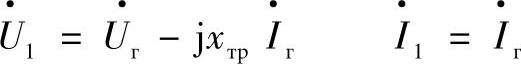
中间点上装设一个电抗器的线路如图4.9所示。等值二端口网络参数为:
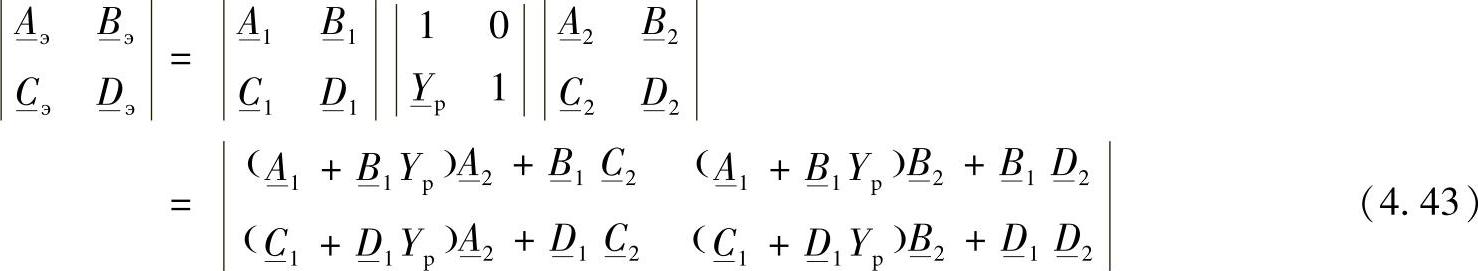
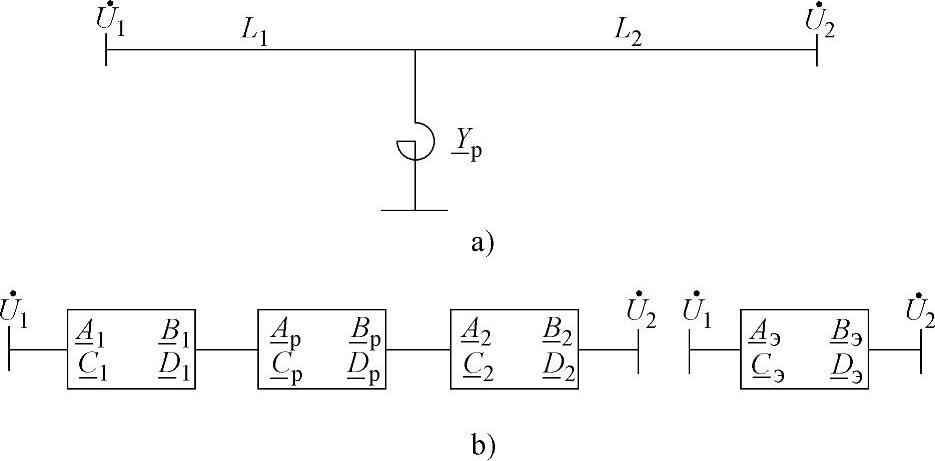
图4.9 装设一个电抗器的线路a)以及其等值二端口网络b)(https://www.xing528.com)
将等值二端口网络参数的表达式展开为:
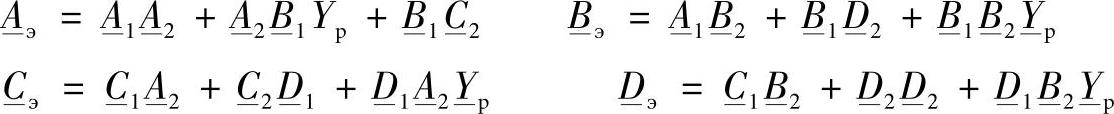
将理想线路子二端口网络参数的表达式代入,并且计及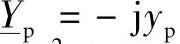 ,变换后得到:
,变换后得到:
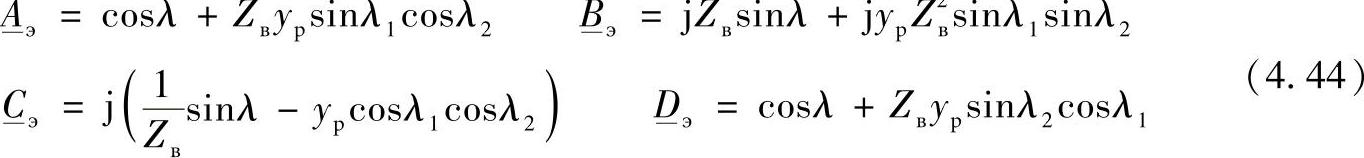
注意到,当输电线路中间某点上连接电抗器时,Bэ>B0,说明线路的输电能力降低;而当电抗器连接于任何一个端点上时,Bэ=B0,此时的输电能力并没有减小。这可以作如下解释,由于未考虑电源的内部阻抗,线路首端和末端的电压是不变的。
当电抗器的容量较大时,等值二端口网络的参数由表4.2所列出的电路确定。
中间点上装设纵向的容性无功补偿装置(没有电抗器)的线路(如图4.10所示)。等值二端口网络的参数:
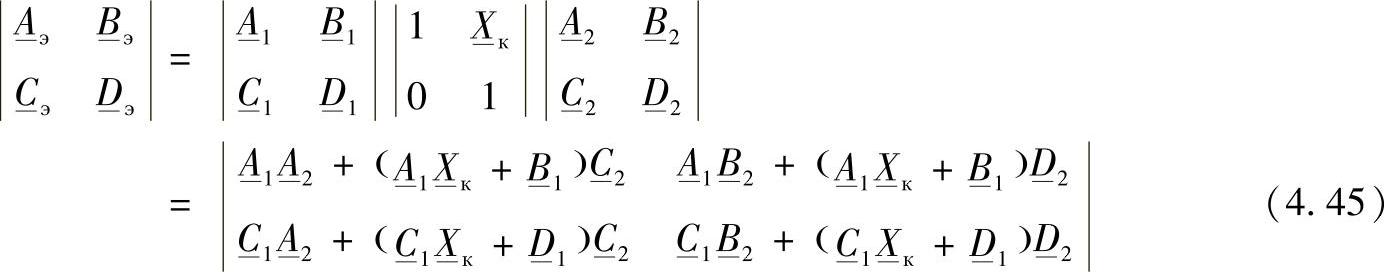
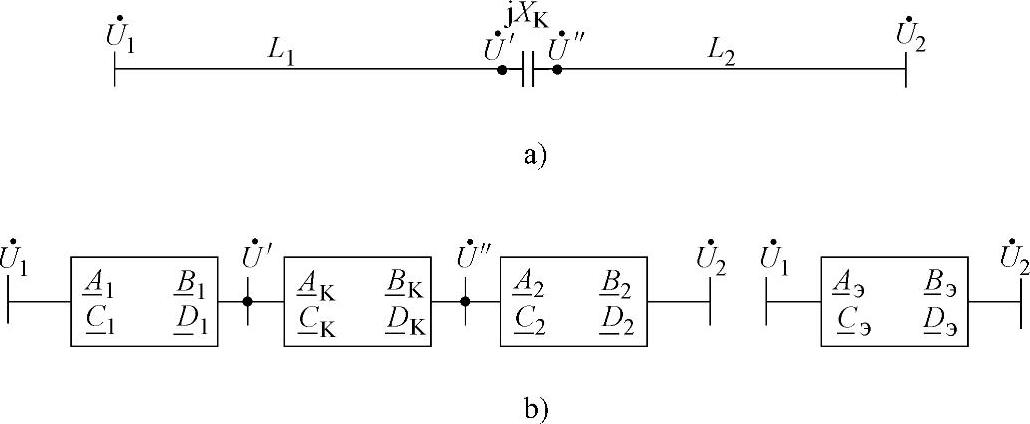
图4.10 无电抗器的可控补偿装置线路a)以及等值二端口网络b)
将各个二端口网络参数表达式代入,并且计及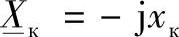 ,对于理想线路最终得到:
,对于理想线路最终得到:
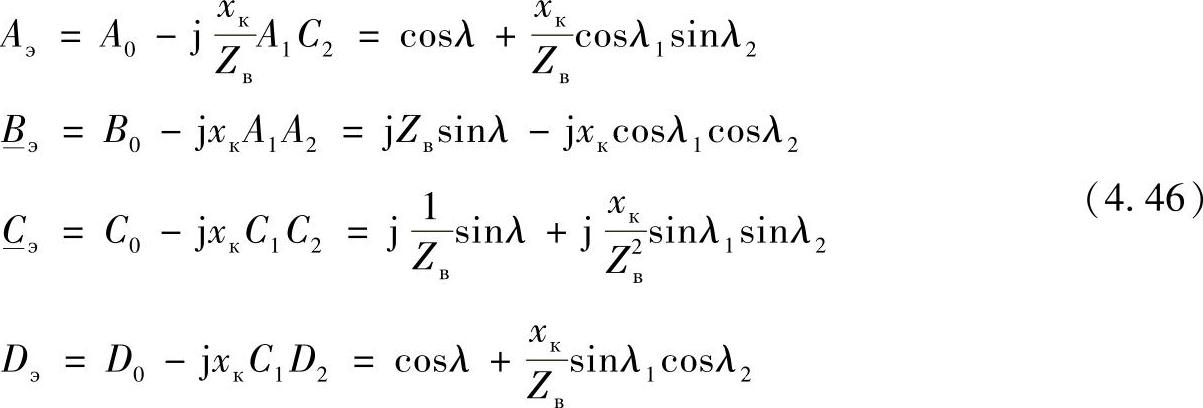
在此不同于上述Bэ<B0的情况,说明输电能力增大。如果计及λ2=λ-λ1,将此值代入Bэ表达式(4.46)中,并且针对l1求导,变换后可以得到:
λ1=λ/2 (4.47)
这说明Bэ取得最小值,换句话说,当xк给定时,最大输送能力将发生在线路的中心点上设置可控补偿装置的情况下。
可以看出,当集中参数元件连接到线路上时,所有的等值二端口网络系数分为两个分量。其一是,相应“自然”线路的常数;其二是与此元件参数(阻抗、导纳)和连接地点有关的附加项。这同样适用于连接了几个集中参数元件的情况,分量数量增加,其中之一对应于“自然”线路,而其他的分量将反应元件参数和连接地点。
图4.11a表示在第一分段带有中间变电站和纵向补偿装置的输电线路图。输电线路的子二端口网络和等值的二端口网络如图4.11,b所示,图中也同样列出了可以得到输电线路中间点状态参数的组合二端口网络的边界。
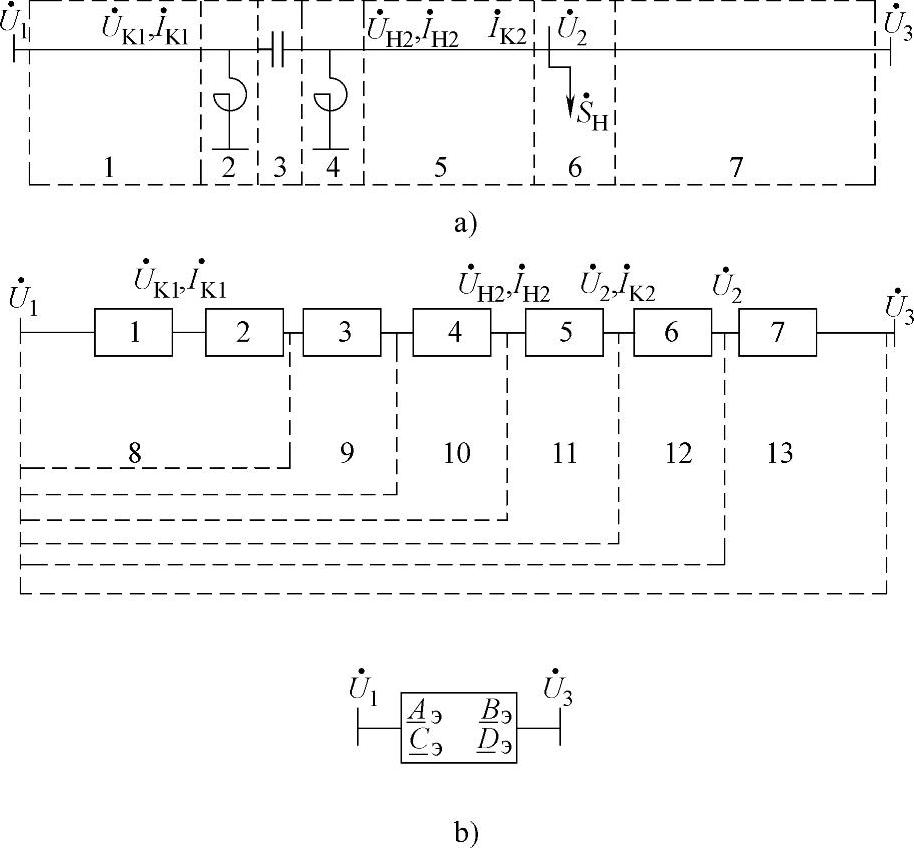
图4.11 带一个中间功率输出的补偿输电线路
a)输电线路示意图 b)等值二端口网络及其构成
在此情况下,等值二端口网络的参数可以由下式确定:

为了检验计算结果的合理性,利用已知的二端口网络方程:
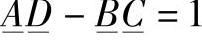
在给定输电线路末端状态参数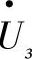 ,
,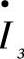 的情况下,首端的状态参数被确定为:
的情况下,首端的状态参数被确定为:

如果输电线路首端的状态参数被给定,那么末端的状态参数可以按照下式确定:

用于求解输电线路中间点状态的组合二端口网络参数,可以通过这些二端口的矩阵累乘积确定。例如,第一条线路(可控补偿装置前面的)第一段终端的电压、电流和功率表示为:

第一条线路(可控补偿装置后面的)第二段首端的电压和电流为:

其中,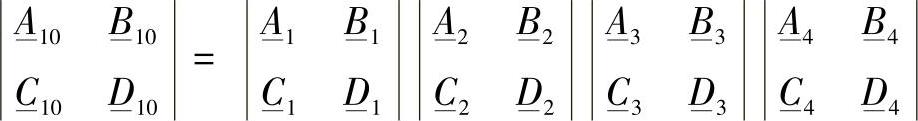
中间变电站母线上的电压、第一条线路末端的电流和功率将等于:

其中,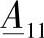 、
、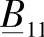 、
、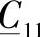 、
、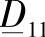 为相应矩阵的导数(见图4.10)。
为相应矩阵的导数(见图4.10)。
输电线路其他所有点上的状态参数都可以以类似的方法得到。在任何一个开关断开的情况下,利用这种方法可以很简单地得到输电线路同步状态参数。当第一条线路首端开关断开时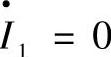 ,由式(4.50)可以得到此开关上线路侧的电压。
,由式(4.50)可以得到此开关上线路侧的电压。
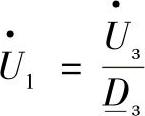
在受端系统开关断开的情况下,即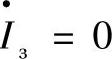 ,此开关线路侧的电压可以由式(4.49)
,此开关线路侧的电压可以由式(4.49)
得到:
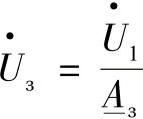
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




