探究Горев方法的有效性

本方法对于确定长度250km～1500km线路等值电路的参数都是适用的。其本质在于，用三角函数替代了复变量的双曲函数表达式，给出了比修正系数法更准确的结果。

Горев方法的主要假设是忽略了电晕电能损耗（g₀=0）。这个假设是合理的，实际上电晕损耗是通过其他方法确定的。

在上述假设下，电磁波的传播系数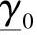和波阻抗Z_в可以写成如下的形式：

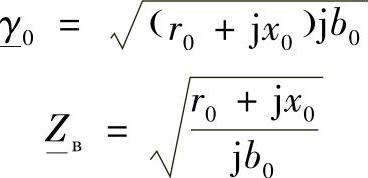
简单的变换后，这些表达式可以被表示为如下的形式：

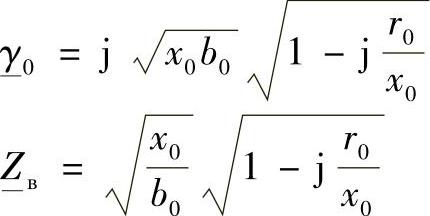
可见，上述两个方程的第一个因子分别对应于理想线路的相位系数和波阻抗，上述两个方程中的第二个因子是相同的。

当x≤1时，为了消掉上述表达式中的根号，将第二个因子表示为幂级数的形式：

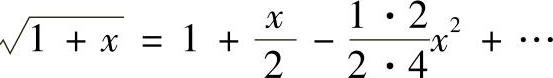
其中

x=-j （r₀/x₀）

如上所述，对于超高压线路r₀<x₀，因此满足x≤1条件。因为较小而忽略二次以上的级数项，得到：

考虑到

因此，此时γ—₀L有如下形式：

其中

表示为两个自变量的函数形式，将有：

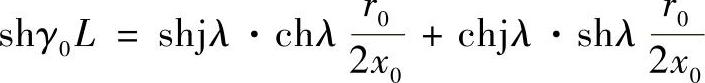
因为λ（r₀/2x₀）≪1，可以采取chλ（r₀/2x₀）≈1以及shλ（r₀/2x₀）≈λ（r₀/2x₀）。除此之外，考虑到shjλ=jsinλ，有chjλ=cosλ。

对ch g₀L做类似的变换，得到：

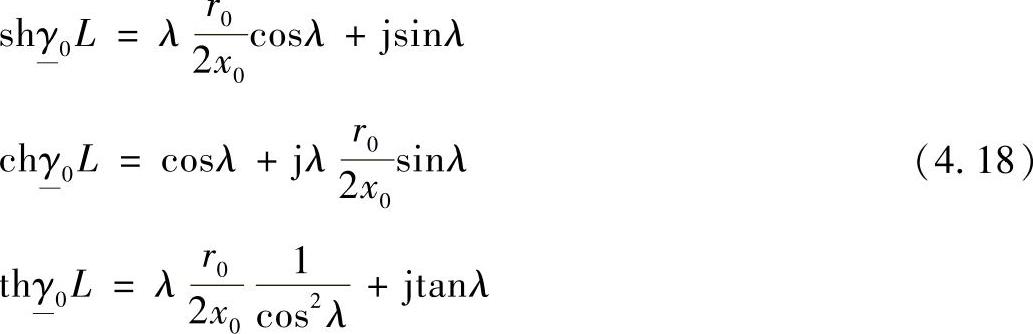
计及式（4.7）、式（4.17）和式（4.18），实际线路П-型等效电路纵向支路的阻抗可以写成：

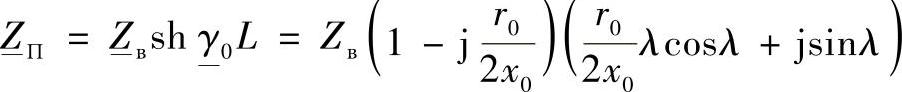
变换后将有：

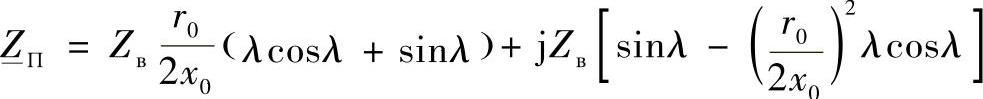(www.xing528.com)

其中

为理想线路的波阻抗。

在得到的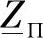表达式中，因为r₀较小，虚部第二项很小，在实际计算中可以忽略。

则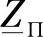表达式被简化为：

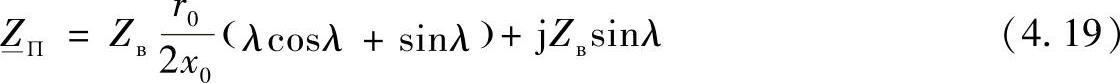
同样，对于П-型等效电路的横向导纳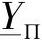可以采取类似的方式确定。省略中间的推导过程，得到—YП的计算表达式为：

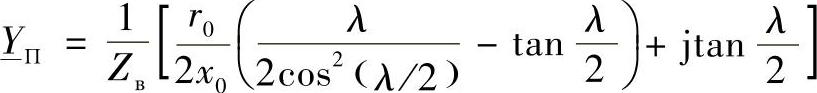
或

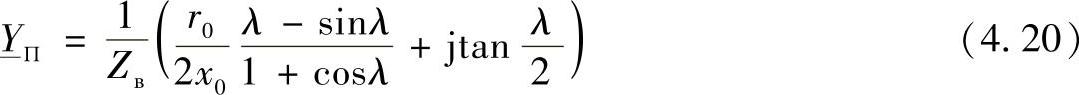
使用此方法也可以得到Т-型等效电路的计算表达式。

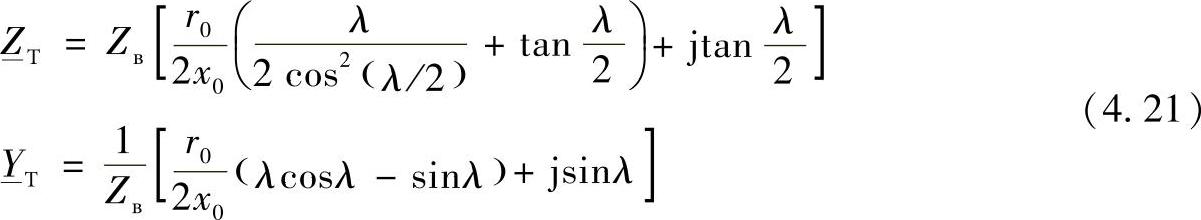
值得注意的是，尽管在按照Горев方法得到确定等效电路参数的方程时，采取了忽略电晕损耗的假设（g₀=0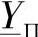），和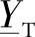表达式中仍存在实数分量。对于相对较短的线路（500～600km），这个分量是很小的，并且在实际计算中是可以被忽略的。但是，随着线路长度的增加（达到1000km或者更长），这个分量增大并必须被考虑。随着线路长度的增加，这个分量补偿了等效电路电阻的不均衡变化，以及此电阻中有功功率损耗的降低。在计算等效电路元件总的功率损耗时，与实际线路中的情况相同。

在设计计算中常常不考虑由于周围环境温度变化导致的导线电阻变化。与参考值相比，电阻的变化在1年当中的不同季节可以达到10%～12%甚至更大，同样引起线路上相应的有功功率和电能损耗的变化。因为超高压输电线路上的损耗较大，应该考虑其电阻的变化。根据要解决问题的不同，可以采取线路敷设地点的年平均气温、一月平均气温、七月平均气温等。

当考虑输电线路电阻的变化时，其单位长度电阻值的变化为：

r₀^t=r₀⁺²⁰（1+0.004（t-20°）） （4.22）

式中 t——计算所采用的、单位为摄氏度的气温。

上面所得到的长线路等值电路参数表达式（4.7），建立了这些参数与线路长度之间的关系，对于使用3×АС—400/51导线的500kV线路，在不计电晕的情况下这些关系如图4.2所示。从中可以看出，等值电路纵向支路的感抗按照正弦规律变化。当线路长度较短时，感抗的增长与线路长度是近似正比关系；当线路的长度接近1500km左右时，感抗的增长变缓并最终停止。当线路的长度进一步增加时，感抗降低并在2930～2980km附近时达到0。同时，容纳急剧增长，当线路长度达到2850km时达到最大值，然后急剧下降，并且在感抗过0时的那个长度上容纳经过0点。所有的这些可以以线路中的波过程来解释。理论上，半波长对应线路的长度为3000km，相应的b₀=0.06°/km。但是，实际上这个值要稍微大一点（β₀=0.0605～0.0615°/km），由此电磁波的长度要稍微小一点。

图4.2 П-型等值电路参数与线路长度的关系

a）电阻rП和电抗xП b）电导gП电纳bП

纵向支路的电阻开始是非线性增长的，并在长度1000km时达到最大；然后降低，并在1900～1950km范围内时过0，并且变为负的。负电阻是违反自然规律的，这意味着线路上不仅无电能损耗，而且还将产生电能，这是不可能的，因为对此并不消耗任何的外部能量。这可以做如下解释。

上面已经表明，在此所介绍的数学模型，只是以与线路两端状态参数相关的方程为基础建立的。因此，此数学模型同样应该给出等值电路或者是二端口网络输入和输出端的准确关系。电阻的降低被横向电导gП实部的增大和其中有功功率损耗的增加所抵消。

在表4.1中列出了gП值的变化与线路长度关系的数据，也同样列出了等值电路两个电导上的总功率损耗。

表4.1 不同长度500kV线路等值电路横向电导和功率损耗

当线路长度为1000km或者更长时，横向电导中的功率损耗变化明显，必须在线路的总功率损耗中考虑。