修正系数法：优化线路参数计算的方法

在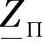表达式（4.7）中，通过线路的单位长度参数表示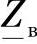，对根号下的值同时乘以和除以Z₀L²，将有：

或

其中

为计及线路参数分布特性的修正系数。

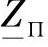当自变量的值较小（线路较短）时，shγ₀L≈γ₀L，。因此，此时等值电路纵向支路的阻抗可以简单地通过单位长度参数与线路长度L的乘积来确定，实际上通常就是这样处理的。但当线路非常长时，的值将明显不等于1，并且这个差别随着线路长度的增加而增大。因此，对于足够长线路，一定要计及系数—k_s。

在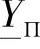表达式（4.7）中也可以做类似的变换，对此表达式的第一项乘以和除以γ—₀ （L/2），并且计及Zв和γ₀的表达式（3.17）和（3.20），变换后得到：

或

其中

为修正系数。

在实际计算当中，如果使用系数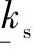和，则计算过程仍十分复杂。因此，可以通过级数分解来简化这些表达式。

双曲正弦函数的级数分解有如下形式：

可以看出，这个级数是不变号的，与正弦函数sin x的级数不同。考虑到x=γ₀L，得到(www.xing528.com)

或

双曲正切函数的级数分解有如下形式：

计及

并且将其代入到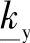的表达式中，有：

或

将表达式（4.13）和（4.14）的实部和虚部分开，忽略二次以上较小的级数项，可以得到为了确定П—型等值电路电阻、电抗和电纳的修正系数：

对于确定电导g_п的修正系数k_g表达式在此没有被列出，因为不是通过线路等值电路电纳的方式来考虑，电晕的电能和功率损耗，而是通过其他方式。

应用这些系数，П—型等值电路的参数被确定为：

在实际的计算过程中，长度为200～250km的线路，修正系数接近于1，因此修正系数被忽略。此时误差不超过1%～2%，对于工程计算是完全允许的。对于更长的线路，必须计及修正系数。应该强调的是，在计算机计算输入支路（长度超过250km的线路）原始数据时，修正系数也是必须被考虑的。

对于长度超过600km的线路，应该使用其他方法确定修正系数，因为在得到表达式（4.15）时（级数分解以及忽略二次以上项）所采取的假设导致明显误差。也就是说，在长度250～600km范围内的线路可以使用此修正系数法。