在第3章中,利用长线路方程已经分析了电力传输的一些特性。根据这些方程可以得到线路在电力传输过程中的一些主要规律,确定主要状态参数的分布,得到一些计算表达式以及建立线路的功率圆图。
但如果应用这些复变量的双曲函数方程去计算复杂电力系统的状态,实际上会使问题更加复杂化。除此之外,在计算复杂电力网络状态时,同样需要得到线路两端的状态参数和电压。为了解决上述问题,可以采用其他的方法,使用另外的线路数学模型:等值电路或者二端口网络模型(见图4.1)。
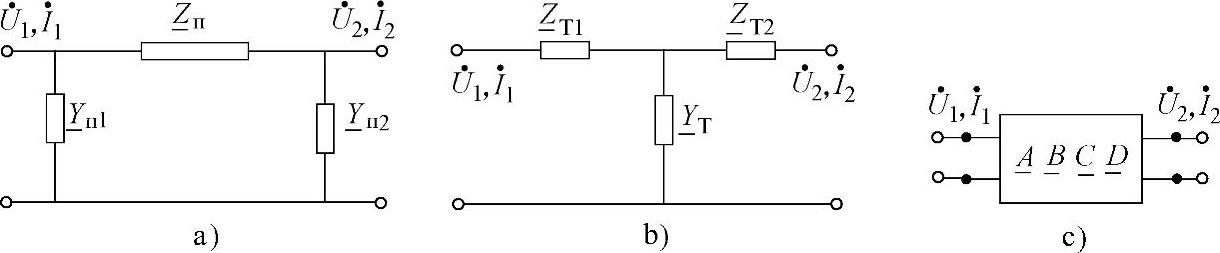
图4.1 可能的输电线路模型
a)П—型等效电路 b)Т—型等效电路 c)二端口模型
现在已有的输电线路等值电路模型包括:П—型等效电路,Т—型等效电路,Г—型等效电路。在实际的电力系统计算过程中,使用最多的是П—型等效电路,其次是Т—型等效电路和Г—型等效电路。
在实际的复杂电力网络状态参数计算过程中,二端口模型同样没有被广泛使用,但是在远距离输电的计算过程中,除了分布参数线路以外还必须考虑电抗器、纵向补偿装置和其他一些集中参数元器件时,采用二端口网络比等效电路的计算更快、更简单。
应该注意到,等值电路和二端口网络都是数学模型,只能得到这些模型输入和输出端点上的值,任何中间点上的功率和电流均不是状态参数的映射,也不能用任何仪器测量,因此这种模型的使用仅仅是一个计算的手段。
因为长线路方程是所有线路状态计算方法的基础,所以这些方程和所使用的线路模型参数之间的关系是很重要的。
与结合线路两端状态参数的无补偿线路方程相对照,二端口网络方程可以描述为:
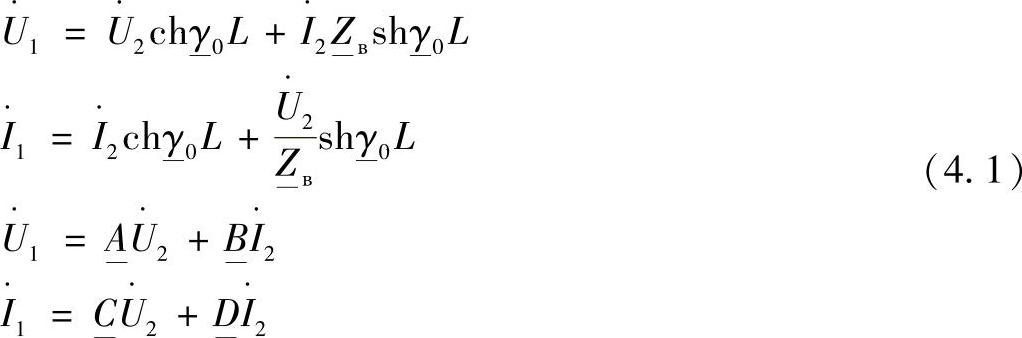
由此,对于实际的线路有:
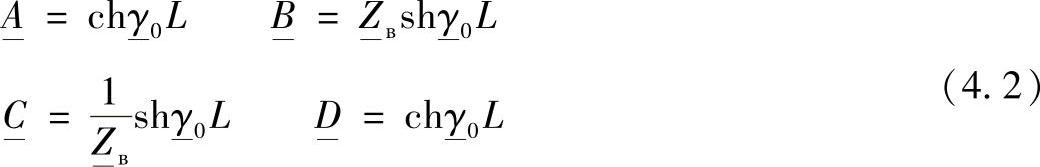
对于理想线路有:
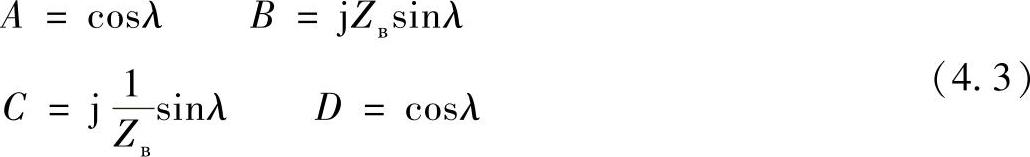
下面分析二端口网络参数与П—型和Т—型等效电路参数之间的关系。考虑通用性,在此对不对称的П—型等效电路和Т—型等效电路进行分析。即:对于П—型等效电路,其两个横向的电导不相等(—YП1≠—YП2);对于Т—型等效电路,其纵向支路的两个阻抗不相等(Z—Т1≠Z—Т2)。这种参数之间的关系不只是在线路的等效电路中被碰到,对其他各种集中参数元件的等效电路同样适用。包括输出端带不同电抗器的纵向容性补偿装置等效电路,具有不同绕组阻抗的自耦变压器等效电路等。那么,对称等效电路可以作为不对称等效电路的一个特例。
对比不对称的П—型等效电路和二端口网络,在空载(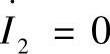 )情况下可以得到:
)情况下可以得到:
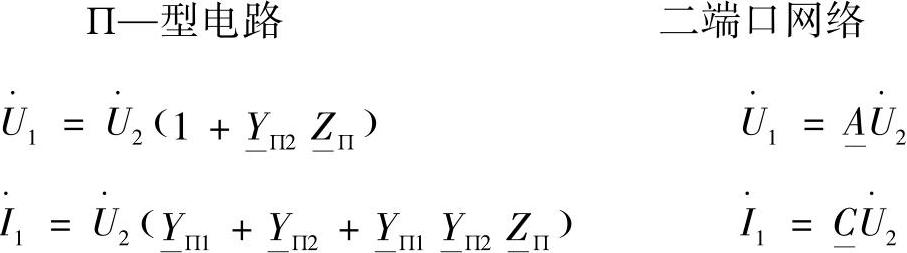
在短路情况下(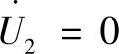 ),可以得到:(https://www.xing528.com)
),可以得到:(https://www.xing528.com)
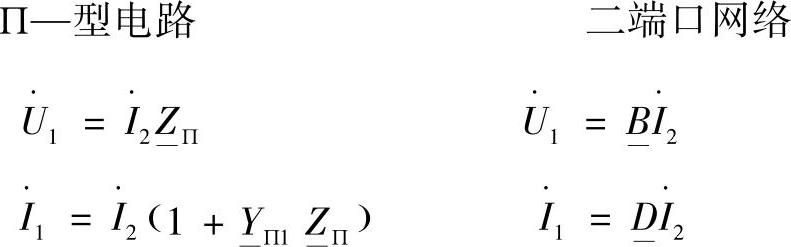
对比结果,可以得到以不对称П—型等效电路参数表示的二端口网络系数
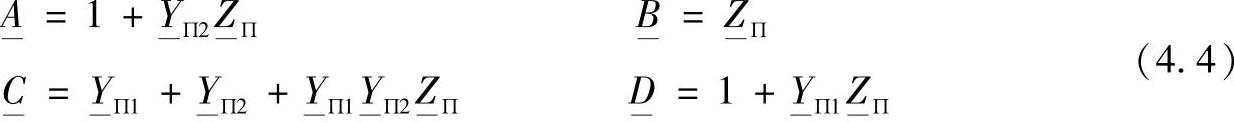
对Т—型电路进行类似的短路和开路试验,可以得到:
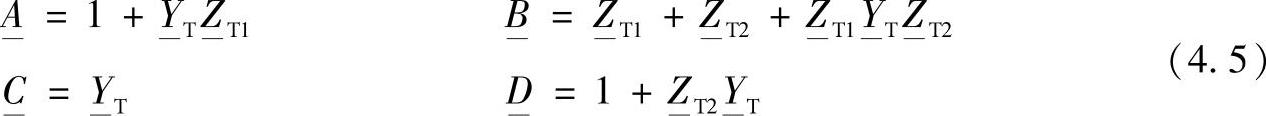
对对称的线路П—型等效电路,令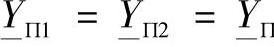 ,在式(4.4)基础上得到:
,在式(4.4)基础上得到:
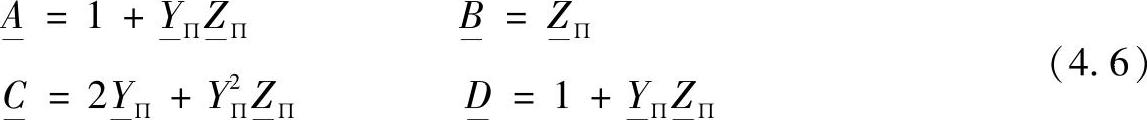
计及式(4.2)和式(4.6),实际线路П—型等效电路的纵向电抗和横向电导有如下的形式:
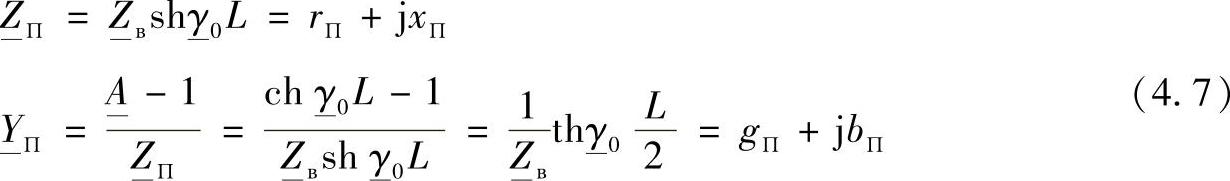
对于理想线路有:

根据表达式(4.7)和式(4.8)得到的集中参数等效电路考虑了线路参数的分布特性。
计及式(4.2)和式(4.5),对称的T—型等效电路线路参数在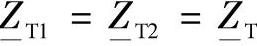 时可以确定如下:
时可以确定如下:
实际线路
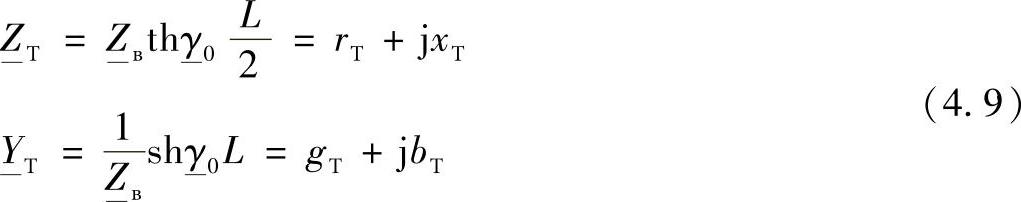
理想线路

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




