如何优化电力线路的无功功率？

上面得到了按照理想线路两端数据确定的无功功率Q*1和Q*2方程，根据这些方程只能得到无功功率的近似值。

在理想线路中，导线的电阻，不管有多么小，都将给线路的状态参数带来显著的影响，特别是最终的无功功率值。为了对此影响进行评估，必须得到计及线路电阻的线路两端无功功率方程。

在上面得到的方程组（3.11），将其中的第一个方程重新列出：

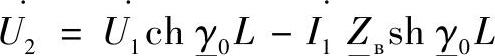
在这个方程中，乘积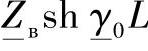是线路П型等值电路^[3]的纵向支路阻抗，可以表示为

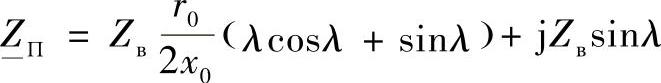
电流I·₁的复数值按照与上述相类似的过程确定

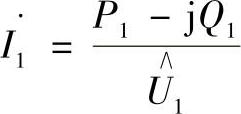
将Z—П和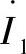代入到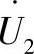中，忽略二次项，变换后得到实际线路首端的无功功率方程：

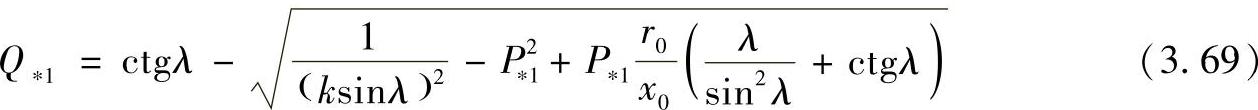
式中，P_*1和Q_*1是标幺值；基准值为。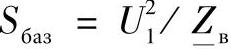

代入Q_*1后，从式（3.69）和式（3.37）中可以得到线路中间点上状态参数的复数值，并且得到以实际线路首端数据表示的参数分布。

类似的变换同样可以应用于式（3.13）第一个方程：

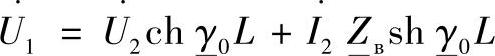(https://www.xing528.com)

其中

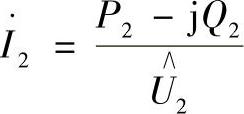
将Z_П和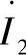带入到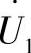的方程中，进行变换后得到实际线路末端的无功功率方程：

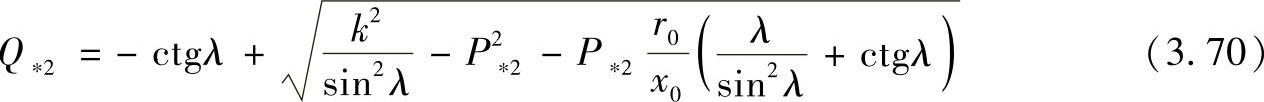
其中，基准值采用S_баз=U²₂/Zв。

得到实际线路的Q_*2值，并代入到式（3.40）中，可以得到状态参数在此线路上的分布。

当在结论中采取一系列的假设后，根据式（3.69）、（3.70）进行工程计算可以保证足够的精度，与实际中其他被核准的方法相比较，误差不超过1%～2%。

对于500kV、500km长度的实际输电线路，在没有考虑电晕情况下的无功功率Q*1和Q_*2与r₀/x₀的关系如图3.11a、b所示。自变量（r₀/x₀）变化的范围可以由零（对于理想线路）到220kV及以上电压等级线路所使用导线型号具有的r₀/x₀值。例如，对于330kV线路，当所使用导线2×АС-240时自变量的值为0.18；对于220kV线路，使用导线型号为АС-400时也具有同样的值。也就是说，被例举的r₀/x₀值（0.18）是单芯导线和分裂导线之间的边界，比它小的值对应分裂导线，比它大的值对应单芯导线。

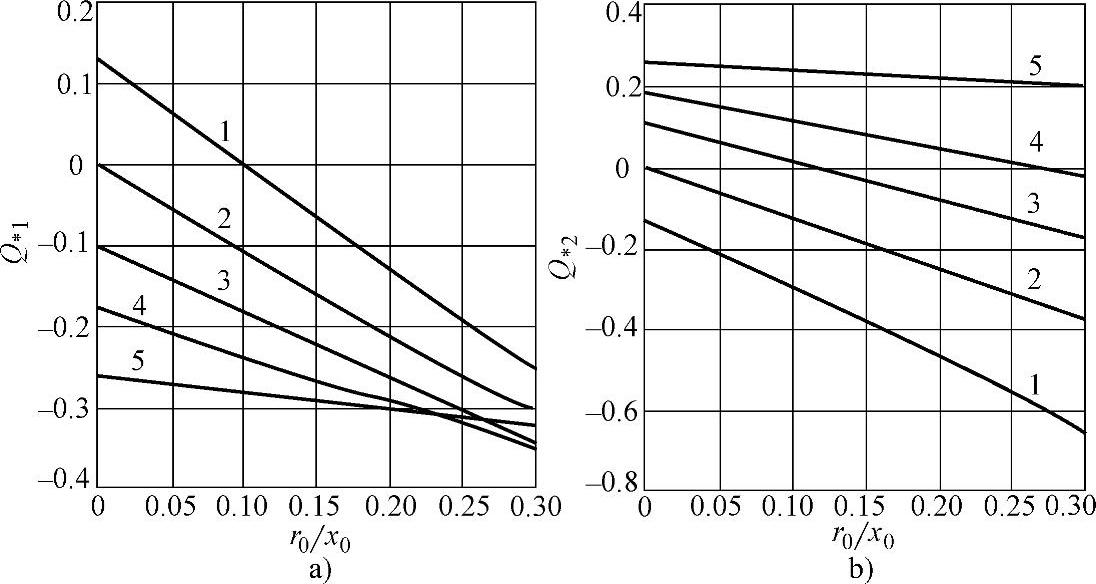
图3.11 当L=500km，U₁=U₂=500kV，x₀=0.308Ω/km， b₀=3.62×10^–6 s/km：1—1.2Р_нат；2—Р_нат； 3—0.8Р_нат；4—0.6Р_нат；5—0.2Р_нат 线路首端无功功率Q_*1 a）和末端无功功率Q_*2 b） 与r₀/x₀的关系

图3.11中所示的关系曲线证明了，导线的电阻对线路末端的无功功率产生了较明显的影响，影响的程度取决于传输功率：大负荷运行方式下影响也较大，在小负荷运行方式下影响也较小。这可以由图3.11中关系曲线的斜率说明。

只有通过输电线路的波特性才能解释这个结果，可以通过线路分段的等值电路（见图3.2）给出比较接近的解释。

线路分段的纵向分支由串联阻抗构成：电阻r₀和电抗x₀。当有功功率由左到右流过电阻时将产生电压损耗，并且点3上的电压降低，结果是在感抗中产生了电压降，点3上的电压比点2上的大，产生无功通流，这与有电压降时理想电路的情况相类似（k＜1）。无功通流与有功功率流相向，即总是负的，这个解释可以被实际线路电压、电流和无功功率分布的曲线图证明（图3.12～3.14）。