理想线路的无功功率计算

线路末端的无功功率与其他状态参数有关，可以由式（3.44）得到线路末端无功功率的计算表达式，将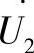移到第一个方程的左侧，得到

将上述方程的左侧和右侧同时进行平方，有：

k²=（cosλ+Q_∗2 sinλ）²+（P∗sinλ）²由此可以得到Q_*2的值。

从式（3.39）的第一个方程中，可以得到计算线路首端无功功率的表达式，进行类似的变换后，有：

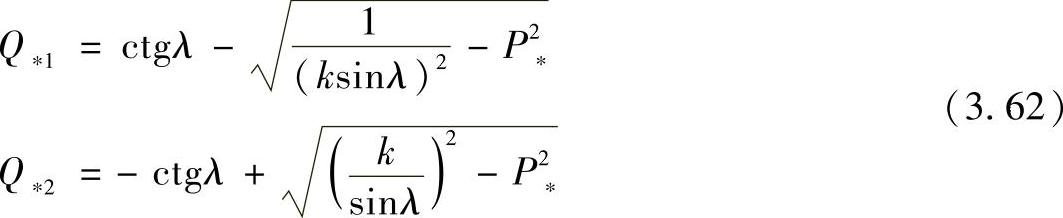
上面已经提到了，对于每个功率圆上的功率P都有两个Q值，因为方根的符号是一正和一负的（±）。在方程（3.62）中，方根成立的条件是δ<90°，两个方程都被表示成标幺值的形式。值得注意的是，两个方程所对应的基准值是不同的，第一个方程的基准功率按照U₁确定，而第二个方程的基准功率按照U₂确定。

在实际的计算中，使用统一的基准功率更加方便，特别是按照线路末端电压U₂确定的统一基准功率。为了得到根据线路末端基准功率确定的Q*1的表达式，可以使用式（3.25）和式（3.56）。

线路末端电流可以被表示为

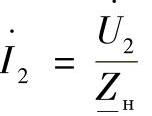
式中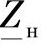，——线路末端的等值负荷阻抗；

将上述电流表达式代入到式（3.25）的第一个方程中，有

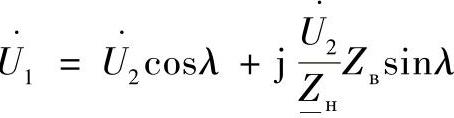
将Zв/Z—н的关系表示为

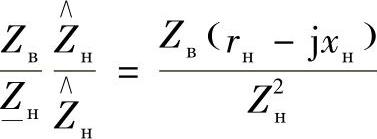
将其代入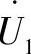的方程中，得到

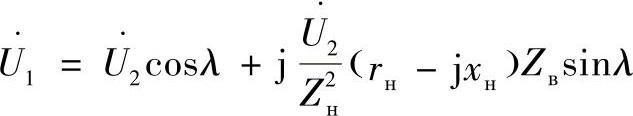
以上述表达式替换功率圆方程（3.56）的，变换后得到：

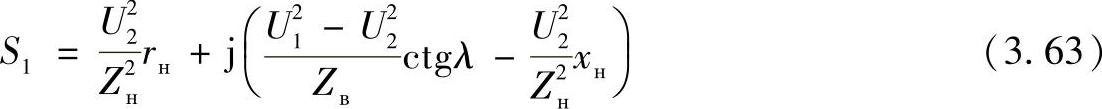
在这个方程中，实部是线路末端的有功功率，等于负荷功率，因为在此分析的是理想线路，所以也等于线路首端的功率，即P₂=P₁。方程的虚部是线路首端的无功功率Q₁，有两个分量，其中第二个分量是负荷的无功功率，即线路末端的无功功率Q₂。

由此线路首端的无功功率可以表示为：

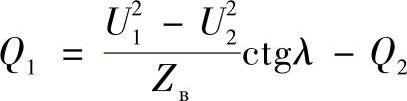
或者(www.xing528.com)

在标幺制下，这个表达式有如下形式：

Q_∗1=（k²-1）ctgλ-Q_∗2 （3.65）将式（3.62）中的Q_*2代入，最终得到

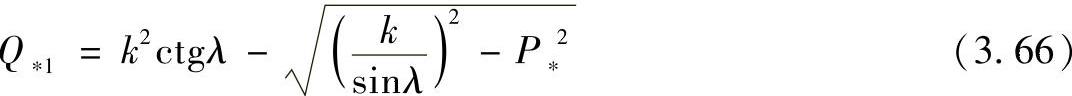
其中，方根符号“-”成立的条件是δ＜90°。

式（3.64）和式（3.65）右侧第一项不是无功功率，是由线路本身内部流程所确定的所谓的“无功通流”，只是当k¹1时才能产生，即线路两端存在电压降的情况，它的产生取决于两个因素。第一个、也是基本的因素是，无功功率由线路外部的电源产生，发电机和同步补偿器等，结果是提高了线路首端节点的电压，也因此产生了无功潮流，例如由远方发电厂的发电机到受端系统。此时线路中产生了额外的有功功率损耗。关于此潮流的合理性问题，应当单独考虑其技术经济指标。

第二个、也是次要的因素是，对邻近更高电压等级节点的线路分段上所产生的容性无功功率升高了。

电压降对理想线路无功功率分布的本质影响如图3.10所示。当k＞1时，与k=1时的情况相比，通流使无功分布曲线图的位置向上移动了，结果是当Р＞Рнат时Q₁的值增大了，Q₂的值减小了；而当Р＜Р_нат时，Q₁的值减小、Q₂的值增大；当k＜1时，通流的方向改变，它的符号也改变了，与k=1时的情况相比，随着Q₁和Q₂的变化无功功率分布曲线图的位置被向下移动。

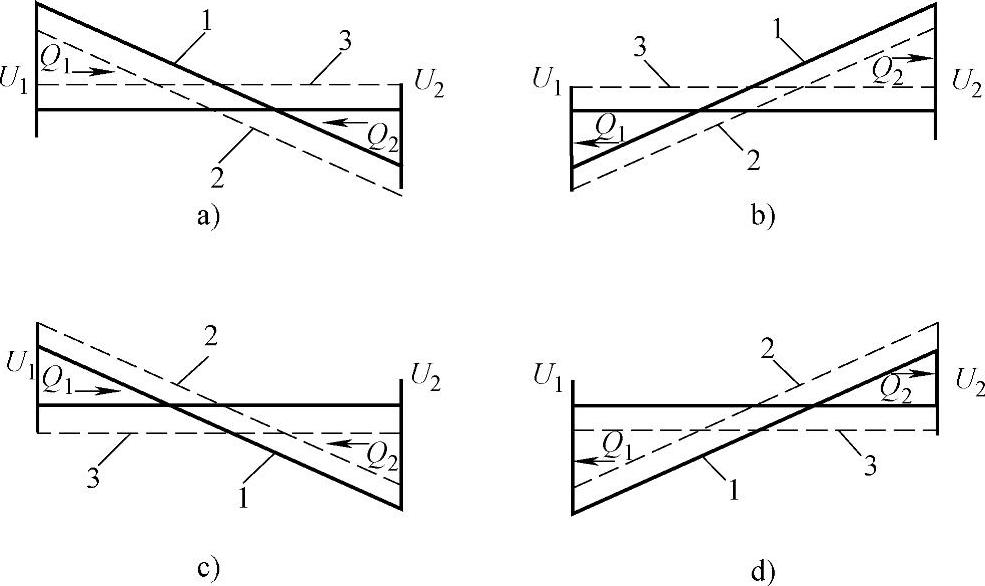
图3.10 电压降对理想线路无功功率分布的影响

a）P＞Pнат，k＞1 b）P＜Pнат，k＞1 c）P＞1，k＜1 d）P＜Pнат，k＜1（1—k＞1时Q分布的曲线图；

2—k=1时Q分布的曲线图；

3—Q通流）

由上述方程可以看出，通流是线路长度的函数。在相对较短的线路上，当ctg l足够大时，很小的电压降都将导致较大的无功通流。例如，对于100km和300km长的线路，当k=1.05时无功通流值分别是0.975和0.315。在第一种情况下，通流实际上等于线路的自然功率，它引起线路有功功率损耗的急剧增加，并且可能破坏线路受端节点的无功功率平衡。对于更长的线路也同样存在这些影响，但是影响的程度较小。所有的这些不利影响都要求通过最优电压降值的选择，并采取相应的措施来使线路正常工作。

式（3.66）和式（3.62）可以变换成如下形式。将右侧第一项移到左侧，两侧进行平方并变换后得到：

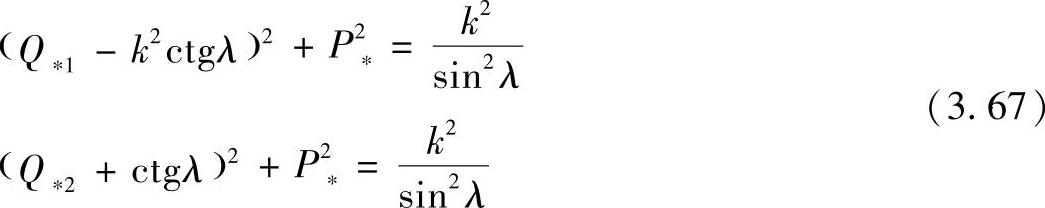
式（3.67）同样也是理想线路的功率圆方程，被描述成与上面方程不同的形式，说明如下。

分布在x-y轴上第一象限的标准圆方程有如下形式：

（x-x₀）2+（y-y₀）2=R² （3.68）

式中 x₀和y₀——圆心坐标；

R——圆的半径。

对比式（3.67）和式（3.68）可以发现，在式（3.67）中，圆心并没有沿横轴方向移动，只是沿纵轴方向移动，并且负号对应于纵坐标正半轴的移动，正号对应纵坐标负半轴方向的移动。换句话说，线路首端功率圆的圆心向上移动，而线路末端功率圆的圆心由坐标原点向下移动，正如之前所阐述的那样。