理想线路功率圆图优化

可以使用功率圆图来说明线路主要状态参数之间的相互关系。对于输电线路的状态计算来说，由于图解法的精度较差而不被使用；但是当线路长度和所传输的功率发生变化时，利用图解法可以方便地解释整个过程的物理本质。除此之外，利用圆图方程可以得到一些有实际应用的计算表达式。

在直角坐标系下的复平面P-Q上，线路首端和末端的有功和无功功率与角度δ的关系被称为功率圆图。在方程（3.25）中，从第一个方程中得到电流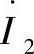，代入到第二个方程中，变换后得到电流相量I·₁：

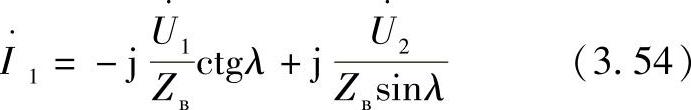
I₁的共轭电流相量为：

线路首端的全功率等于：

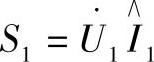
或者

设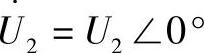，将有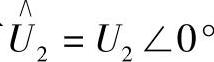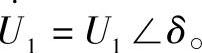，此时线路首端的功率圆方程为

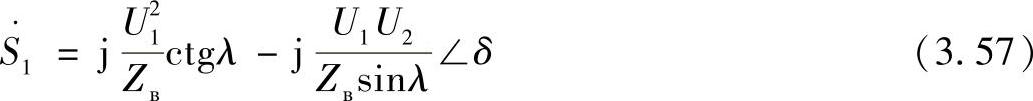
如式（3.57）所示，全功率相量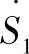是两个向量的差

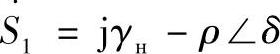
功率圆如图3.8a所示。

向量γн的末端是圆心，对于理想线路来说圆心分布在虚轴上，其坐标由式（3.57）第一项确定。上式第二个向量的模取决于线路末端的电压和线路长度，这个向量是圆半径，其起点是圆心，位置由角度δ确定，它同样也是向量半径ρ，当δ=0°时是沿着虚轴分布的，终点指向下；随着角度的增加、在0～360°范围内变化时，这个终点描绘出一个圆，其中因为向量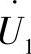是电压相量，半径的旋转是在正方向上进行的，即与时针的选取方向相反。

在实轴和虚轴上，向量半径的投影决定了线路首端的有功和无功功率值。线路可以传输的极限功率对应的δ=90°，所以向量半径的数值决定了P_max。

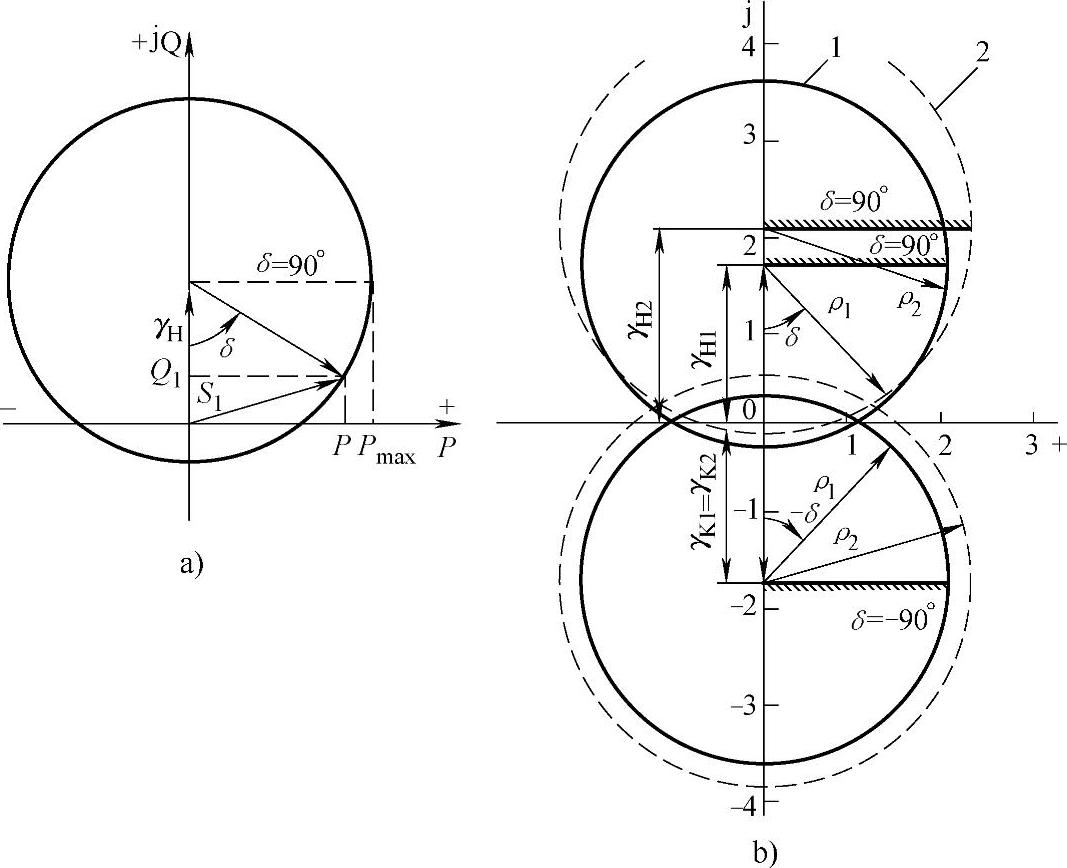
图3.8 无补偿线路功率圆图

（a）线路首端 （b）不同电压降落时线路首端和末端的合成图：1-k=1；2-k=1.1

可以看出，功率圆上的每个有功功率值对应两个无功功率值，但只有在范围0≤δ≤90°变化的那个点对应的无功功率值是有效的。

利用式（3.23）以及运用如上所示的变换，可以得到线路末端的功率圆方程：

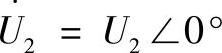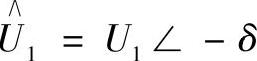在和时，有

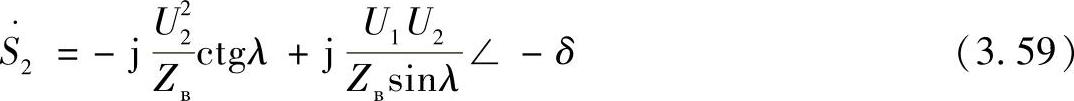
或者(https://www.xing528.com)

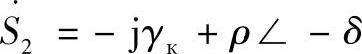
线路的功率圆也可以写成标幺值的形式，为此提出电压跌落度k·，为

通常，k·是复数的形式，但是在常规的计算中被取为电压U₁和U₂模的比值：

k=U₁/U₂考虑到，U₁=kU₂和U²₂/Zв=Pбаз=Рнат，得到：

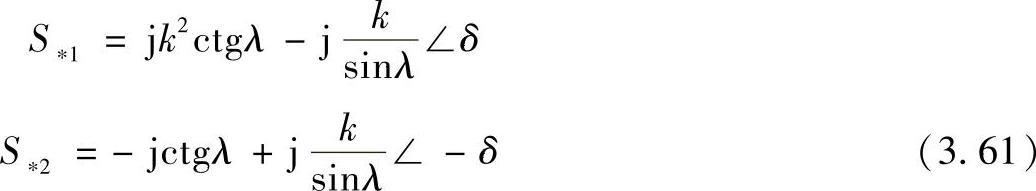
在不同电压跌落度k下、500km长的500kV无补偿线路首端和末端的组合功率圆如图3.8b所示。在此图上功率圆是以标幺值的形式给定的，标记“1”对应k=1时的值，标记“2”对应k=1.1。

线路末端功率圆与首端功率圆的区别如下：

1）线路两端功率圆的圆心γ_к1和γ_к2坐落在虚轴的负半轴上，其坐标由线路长度决定；

2）对于线路末端功率圆，角度δ的计算是在反方向上进行，即按照时针旋转的方向；

3）在线路两端电压相等的情况下（k=1），线路首端和末端功率圆的圆心与线路首端的距离是相等的（γ_н1=-γ_к1），向量半径的值也是相等的（ρ₁=ρ₂）。

当线路的电压降落度k>1时，线路首端功率圆的圆心γ_н2沿着纵坐标轴向上移动，线路末端功率圆的圆心γк2的位置不变（在U₂=常数时）。同时线路首端和末端向量半径的值发生变化，但它们仍然是相等的。

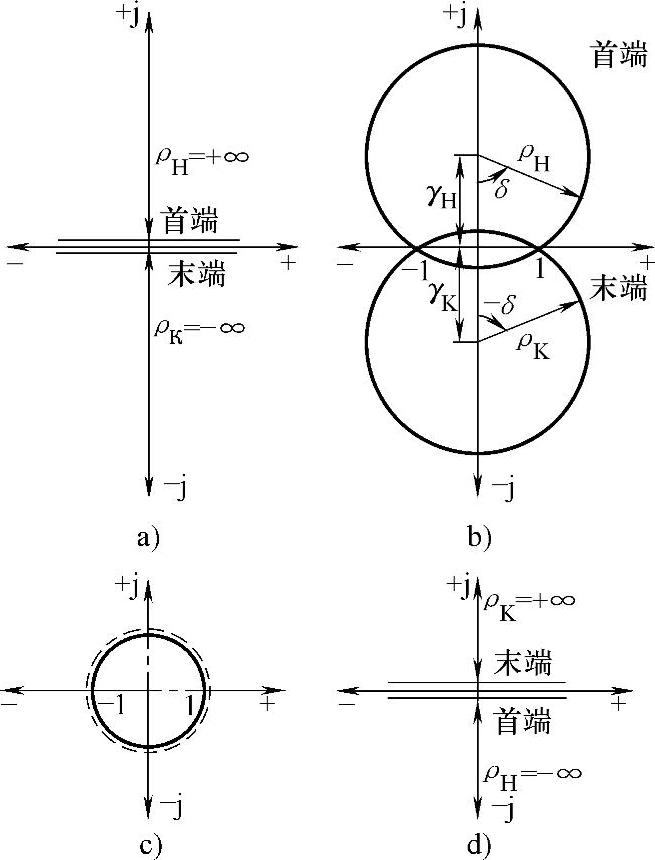
图3.9 长度由0～3000km变化时线路的功率圆

a）L=0 b）L<1500

c）L=1500 d）L=3000km

由此可以得出结论，电压降的变化只是对线路首端功率圆的圆心位置产生影响，对线路末端功率圆的圆心位置不产生影响。除此之外，电压降的变化还影响线路首端和末端功率圆向量半径的值，也同样对线路的传输能力产生影响。

应该说明的是，两个功率圆在k=1时交叉于横坐标轴的点P_*=1上，此时Q_*1=Q_*2=0，所传输的是自然功率。

下面分析当线路长度由0增加到3000km时功率圆的变化。两个功率圆的参数——向量半径和圆心位置，取决于线路长度。当线路长度为0时（λ=0；ctgλ=∞；sinλ=0），两个圆的圆心的位置分别趋向于±∞，向量半径的值同样也是无穷大的。因此两个功率圆退化为横坐标轴上直线（见图3.9a）。

随着线路长度的增加，功率圆的圆心向坐标原点移动，而向量半径的值逐渐减小，说明线路传输能力降低（见图3.9b）。

当线路长度为L=1500km时（线路的1/4波，λ=p/2），两个功率圆的圆心重合于坐标原点，向量半径由电压跌落度k的值确定。当k=1和δ=90°时，两个功率圆交叉于坐标横轴的点P*=1上，这就证明了之前得到的结论，即在此长度上P_max=Pнат（见图3.9b）。

当线路长度继续增加到1500km<L<3000km时，功率圆的圆心继续向坐标原点方向移动，因为在此长度范围内ctgλ<0。此时线路首端和末端的功率圆图发生了变化：线路首端功率圆的圆心向负半平面转移，而末端功率圆的圆心向正半平面转移。值得注意的是，每个圆上的工作区域并没有被改变，因为在指定的长度范围内sinλ>0，并且功率圆方程（3.57）和（3.59）的第二项并没有改变符号。这将使得线路状态与长度小于1500km线路的状态相比变化很大。

当线路长度达到3000km时，两个圆的圆心都向无穷大方向移动（线路首端功率圆的圆心向-¥方向移动，线路末端功率圆的圆心向+¥方向移动），两个圆的向量半径同样等于无穷大，而圆周本身变成了横坐标轴上的直线。就是说，长度为3000km线路的输电能力等于零长度线路的输电能力，即理论上可以达到无限大。

下面详细阐述长度超过1500km线路的状态。