11500公里长距离线路相量图

根据方程（3.44）可以在复平面坐标下建立线路的相量图，如图3.4所示，此时令。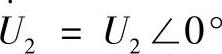

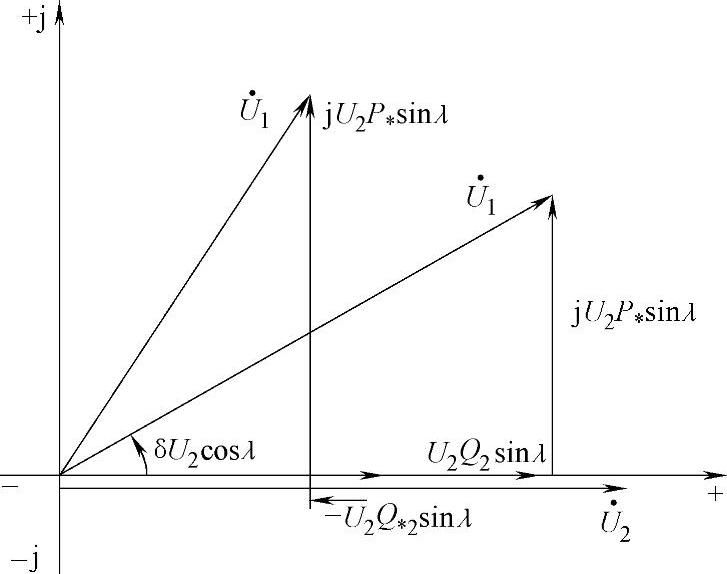
图3.4 理想线路的相量图

此时对应于线路末端无功功率的正方向，所有的实数分布在实轴上，包括Q∗2 sinλ（上图中L≤1500km）。由图3.4，得到

考虑到有功功率的标幺值为

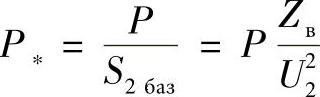
变换后得到

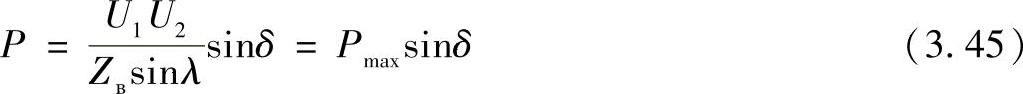
式中 P_max——由线路的电磁特性决定的、线路可能传输的最大功率。最大功率被确定为

从中可以看出，因为交流线路的电抗绝对占优，在电压U₁和U₂模相等的情况下，只有当U₁和U₂之间的相角差为δ时，线路中才能传输有功功率。此时有功功率从超前相量的一侧传输到滞后相量侧。

在式（3.46）中，如果取U₁=U₂=U_ном（此时S_2баз=Р_нат），左侧的第一项除以P_нат，可以得到

传输功率与线路长度的关系如图3.5所示。P_∗max值随着线路长度的增加而降低，当λ=π/2时，相应的L=1500km，极限传输功率等于1，也就是自然功率。当线路长度超过1500km时，极限传输功率也增加了，但是正如下文中所述的那样，功率的增加伴随着一系列不利的现象，使得线路长度为1500～3000km范围内的功率输送变得困难。

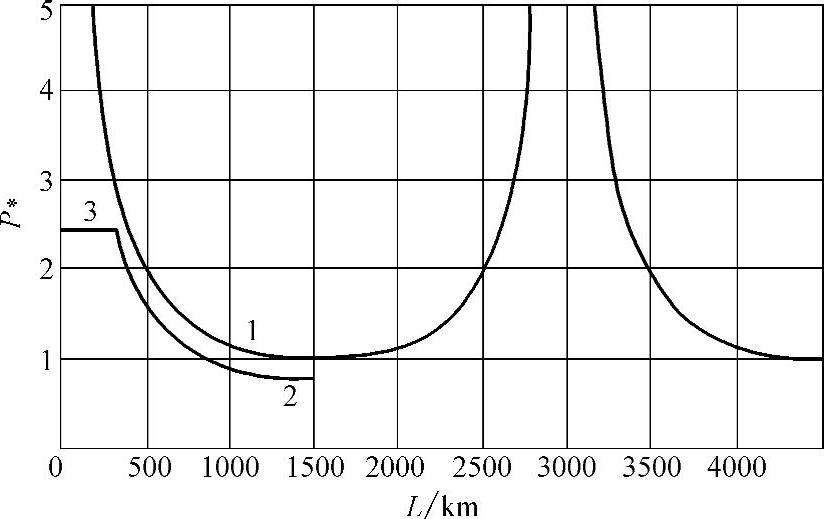
图3.5 极限（1）和最大（2）传输功率与线路长度的关系；导线发热限制（3）

就像在第1章中所表明的那样，针对P∗max，线路的传输能力存在一系列的限制，其中最主要的是导线发热和互联系统的稳定性限制。如果取静态非周期稳定的额定储备系数等于20%，按照这个储备系数，线路可以传输的最大功率Pнб将要略微降低。

稳定储备系数可以按下式计算：

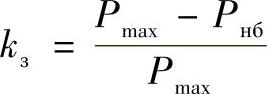
由此，在保持互联系统稳定的情况下，线路可以传输的最大功率为：

Р_нб=P_max（1-kз）

考虑到式（3.47），可以得到

同时，这个最大功率与线路两端电压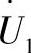和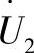之间的角度δнб相对应

Р_нб=Р_max sin_δнб

由此得到

sinδ_нб=1-kз

或者

δ_нб=arcsin （1-kз）=53.1°(www.xing528.com)

δ_нб值与线路的长度无关，上述δ_нб的值只有当U₁=U₂=常数时是适用的，有时角度δ_нб也被称为线路角。

利用上面所得到的表达式和δ_нб，可以建立P∗_нб和线路长度之间的关系（见图3.5），从中可以看出，只有在线路长度为855km时才能传输自然功率（P_∗нб=1），而当线路长度为1500km时，P_∗нб=0.8，也就是说最大功率小于自然功率。而实际上，按照动态稳定性相关要求所确定的线路最大传输功率还要小些。

当线路长度减小时，作为极限传输功率的最大传输功率还将增大，当线路很短时甚至可以达到无限大。但是在实际中，存在导线发热和开关开断能力等方面的限制。对于导线发热限制，其依赖于导线型号和周围环境的温度，最大传输功率通常是在（2.3～3.0）P_нат范围内。

对于短线路，当可以采取sinλ≈λ时，考虑式（3.46）将有如下常用的公式：

早先已经阐明，超高压输电线路的无功功率是其运行状态的最重要指标之一。根据相量图（见图3.4），可以得到无功功率Q₂和角度δ之间的关系，由图可得：

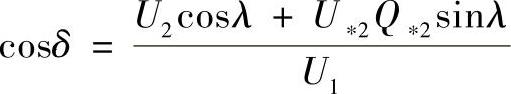
由此确定Q_∗2值后，并考虑到

Q_∗2=Q₂Z_в/U²₂结果是得到了作为δ函数的Q₂表达式

按照线路首端数据及式（3.39）建立相量图后，对于Q₁也可以得到类似的表达式，可以在按照线路首端数据计算状态参数时使用

应该说明，Q₁和Q₂是线路本身直接产生或者消耗的无功功率。

在图3.6中，列出了线路长度小于1500km的关系式Q_∗1=f（δ）和Q_∗2=f（δ），有两个主要特点。其一是这些曲线过0点，与自然功率的传输相对应，此时δ=l（如下所述），可以确定线路的长度；其二是δ=180°的点，此时电压U₁和U₂的相位相反，电流达到了这个线路的最大可能值。但是在正常条件下这个状态是不可能的，只有在互联电力系统异步运行时才是可能的。

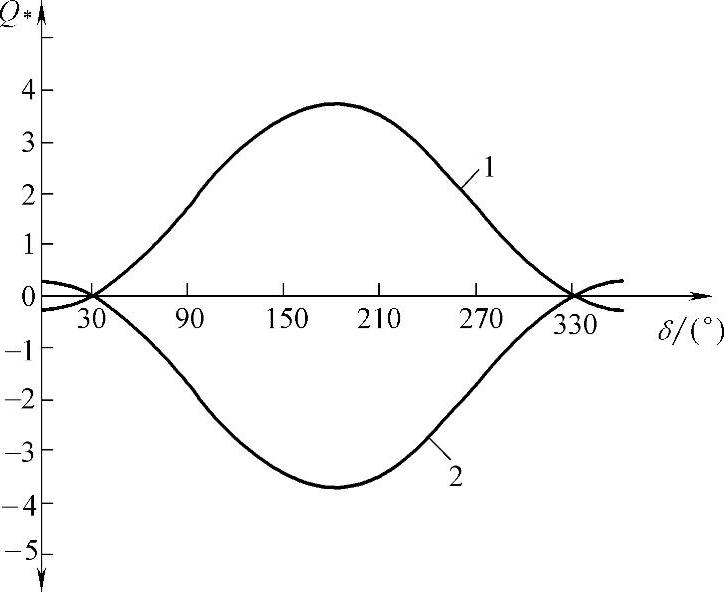
图3.6 线路首端无功功率Q_*1（1）与末端 无功功率Q*2（2）与角度δ的关系

当线路的长度为0时，由式（3.50）可以看出，Q₁=Q₂=0，符合物理意义。

当L=1500km（λ=p/2）时，无功功率为

式（3.50）的第二个分量在此不存在，即ctgλ=0。

当线路长度超过1500km时，式（3.50）的余切符号改变了，Q₁和Q₂已经不是两个分量的差值，而是它们的和，因为L>1500km，δ＜90°（如下所述）。这说明，与L＜1500km时的情况相比较，无功潮流增加了。

根据长度小于1500km线路的相量图（见图3.4），可以找到角度和线路波长之间的关系，取两个直角边的比值，有：

由此可以看出，线路两端电压之间的相角不只与传输的有功功率有关，也与无功功率有关。如果P_*=1，则Q_*2=0，并且此时tanδ=tanλ，或者δ=λ。

那么，当按照理想线路传输自然功率时，角度δ总是等于线路的波长，这可以用来校核最大负荷方式下、当被传输的功率接近自然功率时的状态计算结果。在实际线路的状态计算中，计及导线电阻对δ的影响较小，δ可以增加几个电角度。

当与线路传输自然功率的状态差别较远时，例如在最小负荷方式下，无功功率的影响开始显现出来。不同P*值下角度与线路波长的关系如图3.7所示。

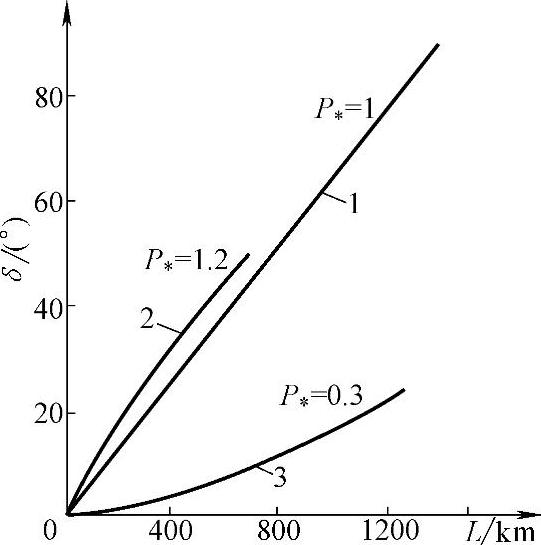
图3.7 P_∗=P∗HaT（1），P_∗＞P∗HaT（2），P_∗＜P∗HaT（3）情况下角度与线路波长的关系