求解3.5长线路的标幺制方程

在上面所得到的方程中，无论是线路首端和末端的状态参数，还是中间点的状态参数中都包含电流相量。同时，在电力系统的状态计算和远距离输电线路的实际计算中，使用的都是功率值。因此，为了计算方便和增加通用性，通过变换到标幺制的方式将功率值代入到式3.10～式3.13中。

首先要规定有功和无功功率的正方向：采取由线路首端指向末端的方向作为有功功率的正方向，而无功功率的正方向与有功功率的正方向是一致的。这说明，在送端，无功功率的正方向是由送端变电站母线指向线路的方向；在受端，无功功率的正方向是由线路指向受端变电站母线的方向。而在一些情况下，线路首端和末端无功功率的方向可能是相反的，此时无功功率的符号变成负的。

接下来推导理想和实际线路状态参数计算的标幺制表达式。

按照实际线路的首端数据计算。

线路首端的复功率在其无功分量是正数的情况下，可以表示为

由此电流相量I₁

将上述电流表达式代入电压方程（3.11）中，对其第二项同时乘以和除以相量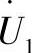，得到中间方程

下面推导线路首端的基准功率。对于实际线路，基准功率是复数值，因为Zв是复数形式

中间方程的第二项除以S₁баз，变换后得到：

将由式（3.32）得出的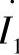代入到电流方程（3.11）中，将这个方程的第一项同时乘以和除以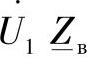，变换后得到

在式（3.34）和式（3.35）中，线路首端功率分量的标幺值等于：

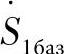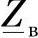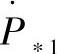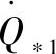应该注意的是，在这些方程中使用的是复数、、γ₀，因此功率和也是复数。

线路末端的功率被确定为

乘以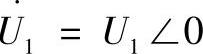，得到

当给定线路首端状态参数P₁、Q₁、U₁时，当前坐标l_x同样表示距离线路首端的长度，则线路某中间点х上的状态参数被确定为

按照理想线路的末端数据计算。与上面的推导过程相类似，通过式（3.22）和式（3.23）的变换可以得到下面的结果。(www.xing528.com)

对于距离线路首端λ_x的某中间点，可以描述为：

其中，P_∗=P_∗1=P_∗2。

对于线路末端有

注意到，P_∗1=P_∗2=P_∗，由于假设r₀=0、g₀=0，线路中没有有功功率损耗。对理想线路，基准功率是实数，且Zв同样是实数

S_1баз=U²₁/Z_в

按照实际线路的末端数据计算。在给定线路末端状态参数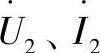时，类似的方程同样可以得到。

以线路末端的电压和功率表示电流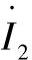后，在式（3.12）中，与按照线路首端数据计算的推导过程相类似，对于距离线路末端l_x距离的某点，有：

对于线路首端有

在式（3.40）和式（3.41）中，功率P*2和Q*2的标幺值按照线路末端的基准条件确定：

式中，。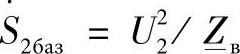

按照理想线路的末端数据计算。对于距离线路末端l_x的中间点，方程（3.40）被写成：

对于线路首端，方程（3.43）则是如下的形式：

在按照线路末端数据计算状态参数时，将相量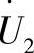作为实轴是较方便的

并且由此可以确定所有量的角度

式（3.37）～式（3.44）确定了线路参数和状态参数之间的关系，从中可以看出，在给定线路参数和电压的情况下，只有当线路两端的无功功率严格确定时，线路中才能传输所需的有功功率。