线路自然功率传输状态详解

线路的自然功率是其最重要特性之一，在此详细阐述这个概念。

对于三相线路中长度为dl的分段，和上面的分析相类似，忽略电阻r₀和电导g₀（见图3.3a）。在某个流过此分段的电流I下，这个分段导线中的无功损耗为：

ΔQ_L=I²x₀ dl

分段产生的无功功率为：

QС=-U²b₀ dl

在上述表达式中，电流是线电流，电压是线电压。

此分段的总无功功率为：

QΣ=ΔQ_L-Q_C（3.27）

上述各个无功功率分量与电流的关系如图3.3b所示。在I=IНαТ时，分段的总无功功率值恰好过0并且符号开始发生改变。这说明在此电流下，这个分段上无功功率是平衡的。线路容性无功功率的产生补偿了感抗中的无功损耗。也就是说，在整个线路的每个分段上，无功功率是相互补偿的。这样的状态被称为自然功率传输状态。在Q_S=0条件下被传输的有功功率被称为自然功率。

与此状态相对应的电流值，当Q_S=0时可以由式（3.27）得到

I²x₀ dl-U²b₀ dl=0

由此

这个电流是线电流，被称为自然电流。相应的相电流可以由下式确定：

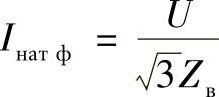
方程（3.28）的左边和右边同时乘以U，得到功率

应该注意到，因为此时Zв是实数值，那么与每相的电压U相对应的电流I同样也是实数值，而S为有功功率。

这个状态是当线路有负载时、等值阻抗等于波阻抗（Zн=Zв）时产生的。此时，线路中无反射波。

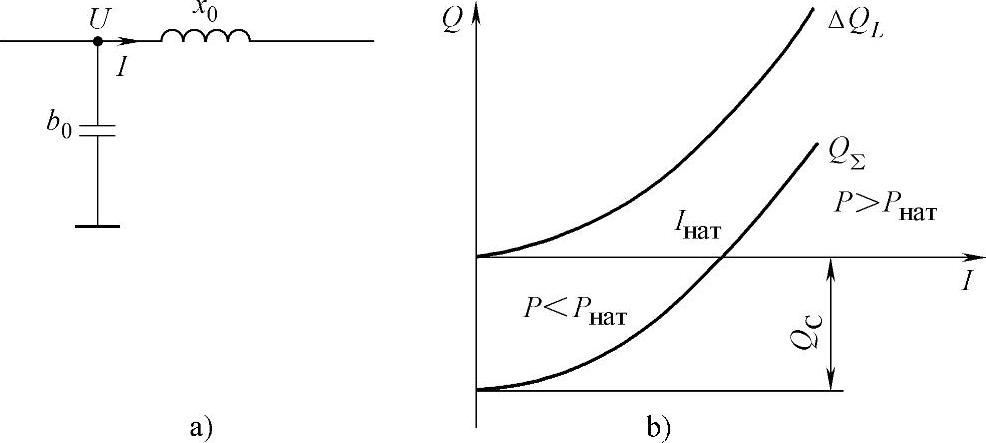
图3.3 理想线路分段上的无功功率

a）分段示意图 b）无功功率分量与电流的关系

如果取线路末段的电压为

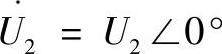(www.xing528.com)

那么线路末端的电流可以由下式确定：

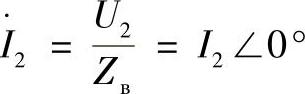
线路末端的功率只是有功功率

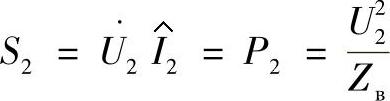
由式（3.24），此状态下中间点的电压和电流为

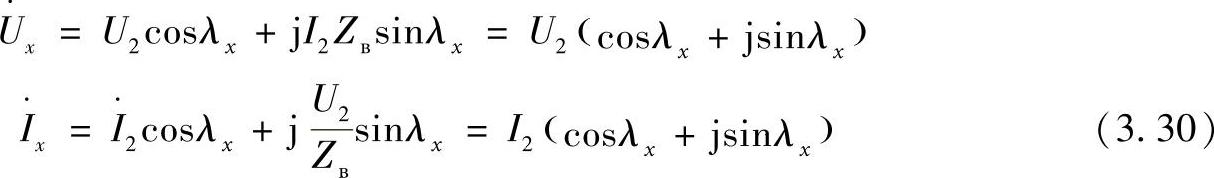
上述方程的右侧第二个因子是相同的，是复平面上的单位圆方程。这说明，在线路的任意一点上，电流相对于此点电压的相位移同样是相等的，并且等于0。也就是说，线路上没有损耗、被传输的只是有功功率，而无功功率在线路所有点上都等于0。

从上述方程中同样可以看出，线路任意一点上电压和电流的模与线路末端电压和电流的模相等，它们只是被向后移动了一个角度，此角度等于λ_x。

由此可以得到两个重要的结论：

1）当按照理想线路传输等于自然功率的有功功率时，在线路任意一点上的无功功率（包括首端和末端）都等于0。因此，不需要任何的补偿装置。

2）电压和电流沿线路是均匀分布的，在线路的中间点上没有任何形式的、需要采取一定措施去消除的过电压。

应该说明的是，这些结论只是对于理想线路完全成立^[2]。当电压U变化时（见图3.3b），线路产生的无功功率也发生改变，因此无功功率的平衡状态被改变，这种情况将在另外一种电流状态下产生，也就是说，线路中传输的是不等于自然功率的有功功率。因此，应该区别对待不同电压下的自然功率值。

在计算过程中，可能使用的是额定电压U_ном、受端系统的电压U₂、最大的计算电压U_{нб расч}或者是最大的工作电压U_{нб раб}，对于所有的这些电压值，其自然功率都是不同的。例如，Р_{нат ном}=U²_ном/Z_в，Р_{нат нб}=U²_{нат нб}/Zв等。

在实际线路上传输的有功功率不是常数，而是在很宽广的范围内随着系统负荷的变化而随时变化的，其变化是由该线路在系统中的作用决定的。在任何一种情况下，线路传输的功率都可能从某个最小值达到最大，此时线路的无功功率平衡条件被破坏。

当线路传输的功率小于自然功率时（Р＜Рнат），即I＜Iнат，在线路上将产生过剩的无功功率，引起线路中间节点电压的升高，此无功功率由线路末段流向邻接的系统（节点）。这将导致一系列不利的影响，因此必须采取措施限制无功潮流和降低线路中间点的电压。其中一种措施是，采用吸收过剩无功功率的电抗器。

当Р＞Рнат时，即I＞Iнат，线路上将产生无功功率缺额，导致线路中间点和线路被连接的系统节点上电压降低，此时需要额外的无功功率电源。因为输电线路传输功率的变化范围是很宽广的，为了保证无功功率平衡，就必须采用不同类型的无功补偿装置。

自然功率表明了线路的输送能力，在波阻抗取平均值的情况下，不同额定电压等级线路的自然功率有如下值：

当然，具体的线路由于长度、结构和一些其他因素上的区别，其输送能力与上述值会有一些差别，这些数值表明的只是输送能力的数量级。

在得到长线路方程时，并没有限定线路的最终长度。因此，这些方程对于任意长度的线路都是适用的。当线路的长度比电磁波的长度小很多时，这些方程也可能有其他的形式。例如，在λ较小的情况下可以认为sinλ≈λ和cosλ≈1，这对于100～150km长的理想线路是正确的，那么以线路末端状态参数表示的方程（3.25）将有如下形式：

同样，短线路是长线路的特殊情况。