理想线路分析：如何确定中间点的状态参数？

当超高压线路使用分裂导线时，每相电阻是随着导线数量的增加成比例下降的，同时每相电抗也减小到了较小的程度。因此，关系式x₀/r₀是随着每相导线数量的增加而增大的，对于目前已经被使用的导线型号和标准的相结构（见表3.1），这个关系式的值在5.5～24.5的范围内。换句话说，对于超高压输电线路，其感抗是占据主要地位的（x₀>>r₀），特别是对于500kV及以上的线路。而对于110～220kV线路，在某些特殊情况下，其电阻和电抗是大致相等的，或者是它们的比值非常的小。

还应该注意到，g₀值主要是由产生电晕时的功率损耗和电能损耗决定的。但是，电晕损耗的计算是采用统计线路首末端功率的方法进行的。这些损耗实际上不影响线路本身的状态参数，包括一些状态下的电压极值。因此，在超高压输电线路的简化计算中可以忽略r₀和g₀，即取r₀=0和g₀=0。此时，衰减系数α₀=0，电磁波的传播系数和波阻抗具有如下的形式：

这使得长线路方程得到了简化，消掉了复变量的双曲函数（双曲函数的计算存在一定的困难），而被三角函数所替代。

在采取上述假设的情况下，双曲函数的变换有如下的形式：shjβ₀L=jsinβ₀L，chjβ₀L=cosβ₀L，同样当α₀=0时，有shα₀L=0，chα₀L=1。由此可以得到：

shγ₀L=sh （α₀+jβ₀）L=shα₀L·chjβ₀L+chα₀L·shjβ₀L=jsinβ₀L

类似地：

chγ₀L=ch （α₀+jβ₀）L=chα₀L·chjβ₀L+shα₀L·shjβ₀L=cosβ₀L

当应用到理想三相线路时，式（3.10）～（3.13）可以被描述成下面的形式。

在现有的线路首端数据基础上，线路中间点上的状态参数可以由下列方程确定：

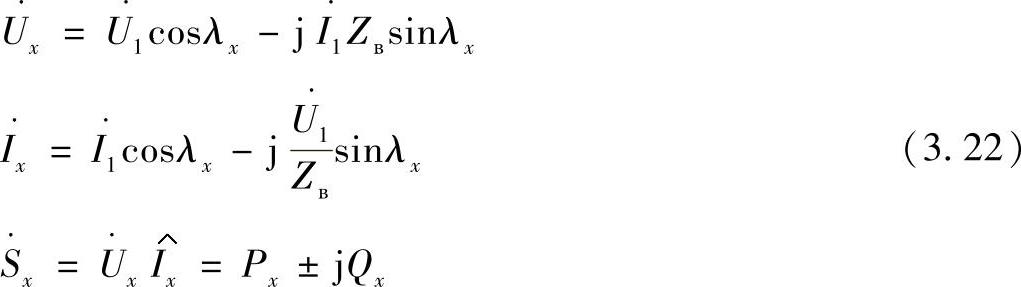
式中 λ_х——距离线路首端的值。(www.xing528.com)

按照首端数据，线路末端的状态参数为：

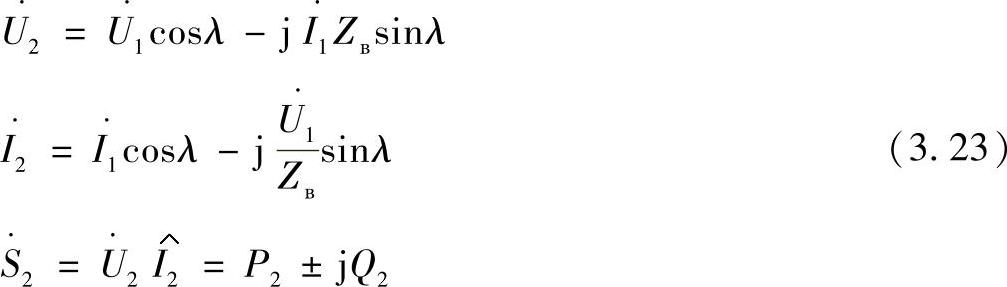
在给定线路末端参数的情况下，线路中间点的状态参数由下列方程确定：

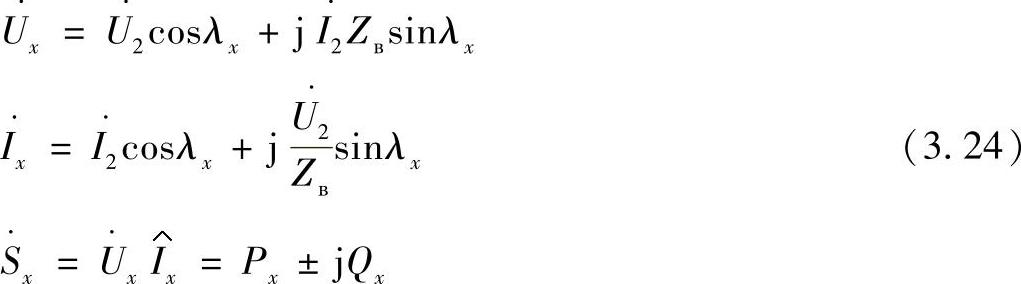
式中 λ_x——距离线路末端的值。

按照线路末端的数据，线路首端的状态参数为：

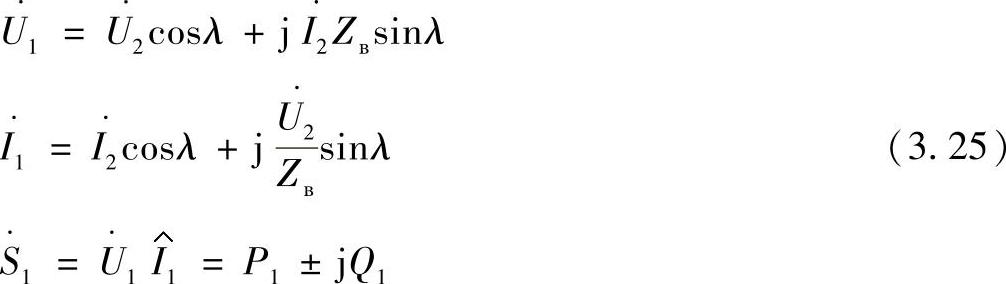
对于理想线路，有功功率在所有点上都是相等的：

P₁=P₂=P_х （3.26）

线路中间点的电压和电流取决于被传输的有功功率值。