长线路分段等值电路对电磁场的描述及其应用

交流线路上的电能传输，实际上是建立线路电磁场的电磁波沿线路的传输。此电磁场有两个组成部分：由导线中流过电流产生的磁场，以及线路相间电压和相对地电压建立的电场。

因为线路的电流和电压是交变的，电磁场的两个组成部分同样也是随时间变化的。电场和磁场的描述如图3.1所示。线路的电气参数——导体的电阻、电感和电容，是沿线路均匀分布的。沿线分布的交流电压导致导线之间以及导线与地之间电容电流的出现。在线路的每个分段，电容电流累加到由传输功率决定的工作电流上，引起线路总电流不断地变化，结果使得每段导线的自感和互感电动势及沿线电压发生了变化。所有这些导致沿线电流、电压和功率值变化规律的复杂性。

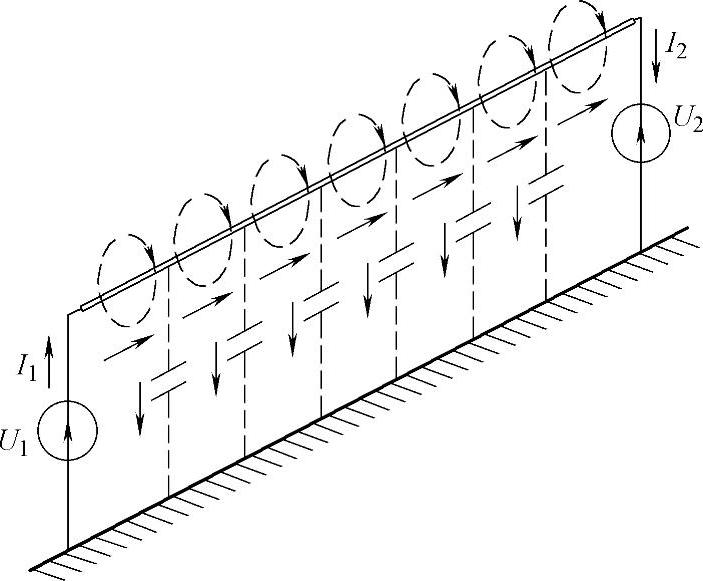
图3.1 沿线电磁场描述

为了确定这些规律性，以长度为dl的一个线路分段为例，此分段距离线路首端的距离为l_x（见图3.2а）。在复杂电力网络中有大量的节点和电源，确定线路的“首端”和“末端”是很困难的，同时为了研究单条线路的特性，这又是必须了解的。因此，在本章及以后章节中规定，有功功率从线路的首端流向线路，再从末端流出。也就是说，线路的首端和末端分别对应有功功率流出和流入的系统节点。

分段的等值电路如图3.2b所示，这个等值电路对于单相和三相线路都是适用的。对于单相线路，通常使用相电压和相电流；而对于三相线路，则使用线电压和线电流。

在分段的边界，电流和电压的关系式可以表示为：

此时考虑到

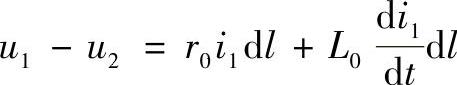
对于节点2，等值电路可以描述为：

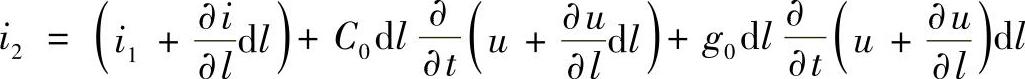
在简单的变换之后，忽略二阶导数，得到：

在方程（3.2）中，所使用的线路电流和电压瞬时值是两个变量的函数：时间和线路的长度。这些方程对于电流和电压随时间的任意变化都是成立的，即对于稳态和暂态都是成立的。

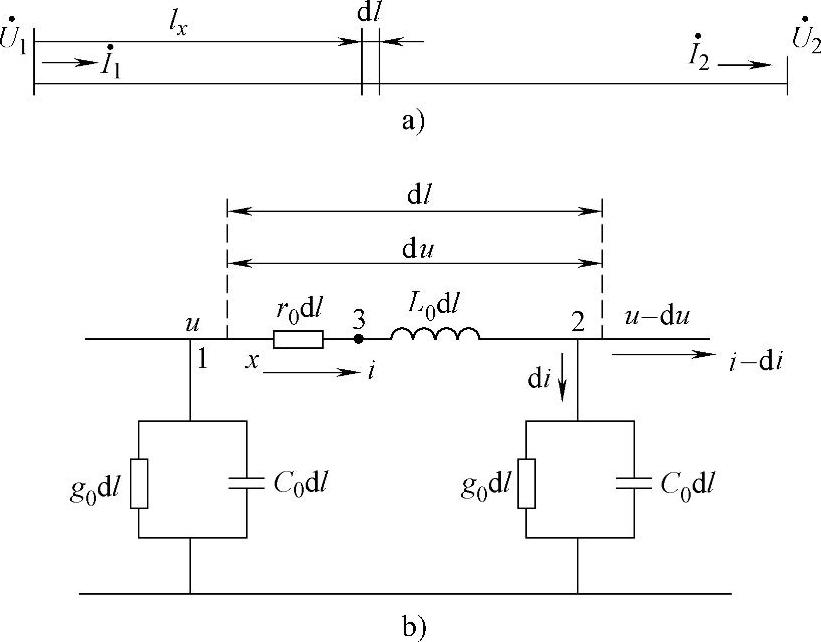
图3.2 线路分段 a）及其等值电路 b）示意图

在电源电压为正弦的情况下，稳态可以描述为：

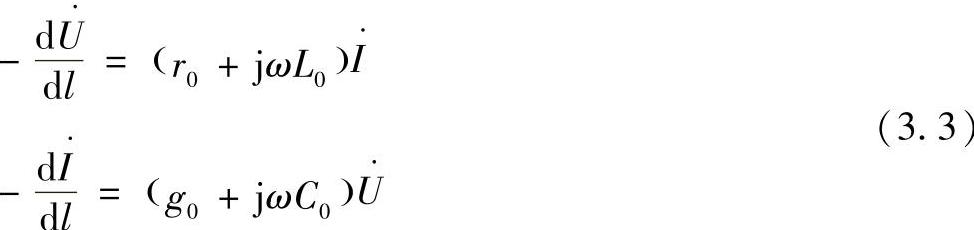
式中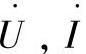——电流和电压相量；

r₀，g₀——电阻和电纳；

L₀，C₀——线路分段的电感和电容。

在此，分段的长度被取为1km是比较合适的。

设线路的单位纵向阻抗为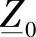及横向阻抗为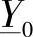，有

式中 x₀、b₀——线路单位长度的感抗和容纳x₀=ωL₀，b₀=ωС₀；

r₀——导线的电阻；

g₀——计及电晕损耗和绝缘泄露时的电纳。

此时方程（3.3）有如下的形式：

将电流和电压对l求导，得到：

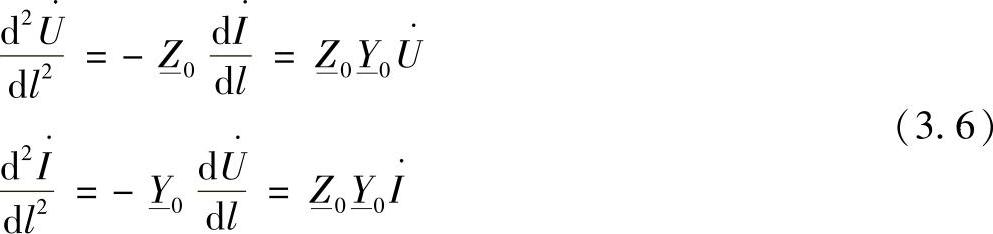
这些方程说明电流和电压是沿线路变化的。

对于距离线路首端为l_x的某点x电压和电流，这些方程的解有下列形式：

电压

考虑式（3.5），电流

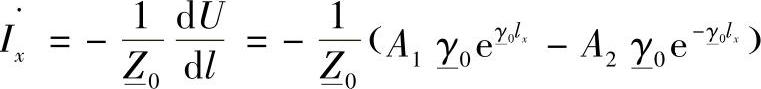(www.xing528.com)

或者

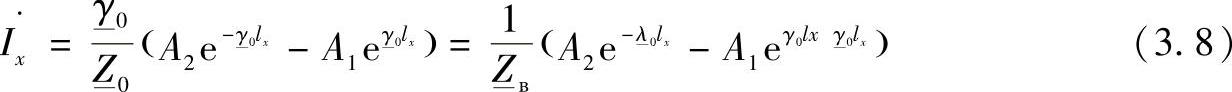
式中 γ₀——方程组（3.6）特征方程的根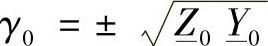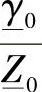；的值可以表示为

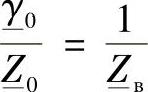
式中 Zв——线路的波阻抗，。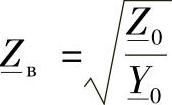

下面解释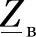和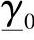的物理意义，在此变量为l_x——当前坐标，积分常数A₁和A₂由初始条件确定。

下面推导计算线路状态参数的表达式。线路首端状态参数的计算。此时，l_x=0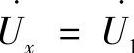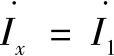，，，或者

解上述方程组，得到：

将A·₁、A·₂的值代入到式（3.7）和式（3.8）中，计算得到

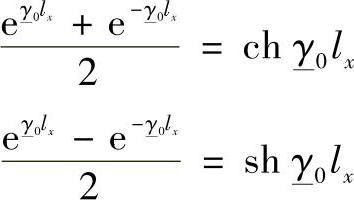
变换后，得到线路中间点х上的状态参数计算表达式：

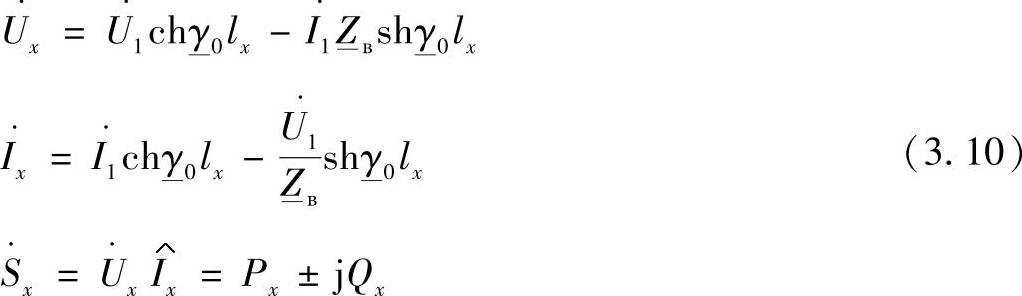
线路末端的状态参数，是当l_x=L以及首端状态参数已知时，按照下列方程确定：

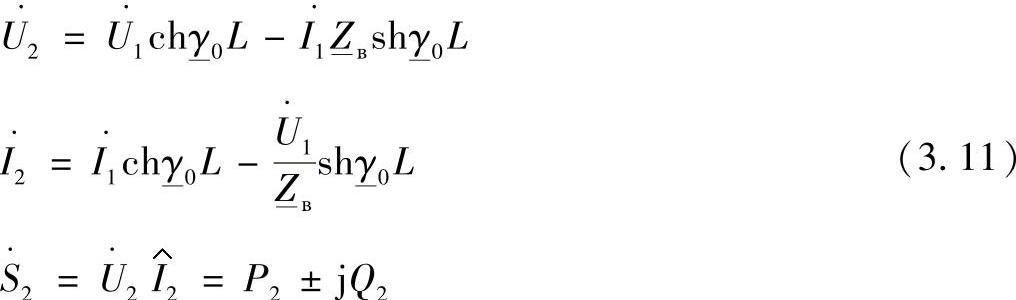
式中 L——线路的总长；

线路末段状态参数的计算。

线路末端的状态参数U·₂、I·₂同样可以被作为初始条件，其中I·₂=S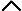2/U₂。此时，当前坐标l_x是在相反方向上展开的，即从线路的末端开始，l_x符号也变成负的。

忽略中间变换过程，在中间点х上的方程可以写成：

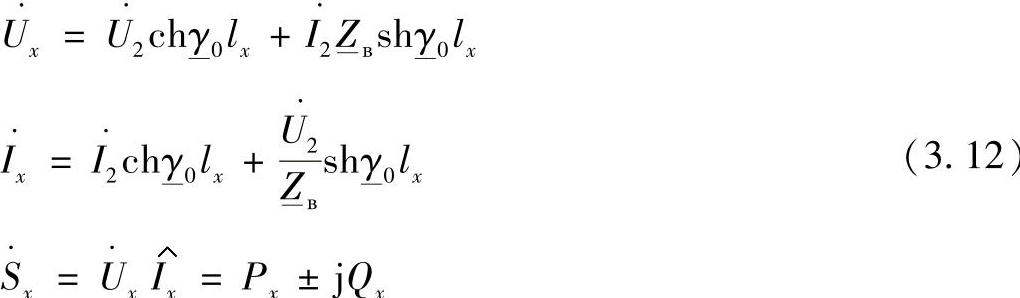
线路首端状态参数与末端状态参数之间的关系，当l_x=L时有如下形式：

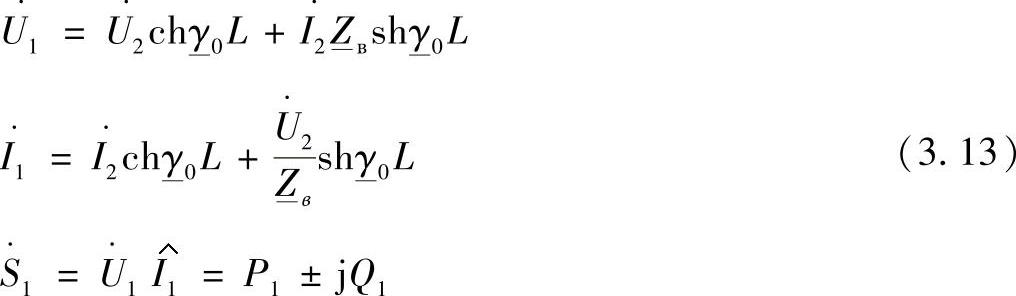
式（3.10）～（3.13）对于单相和三相线路都是适用的。区别只是在于，对于单相线路使用的是相电压和相电流值。而三相线路使用线电压和线电流。除此之外，利用线路单位长度参数x₀和b₀确定波阻抗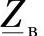和电磁波传播系数γ₀，因为在单相线路中不存在互感和相间电容。

式（3.10）～式（3.13）应用于三相线路时，使用的是线电压和线电流相量，线电流等于

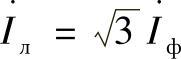
此时中间点x上三相线路的复功率表达式为

式中 I_x——线电流的共轭相量。

在使用三相线路的线电流和线电压时，中间点上的方程（3.10）和式（3.12）有如下形式。

三相线路首端

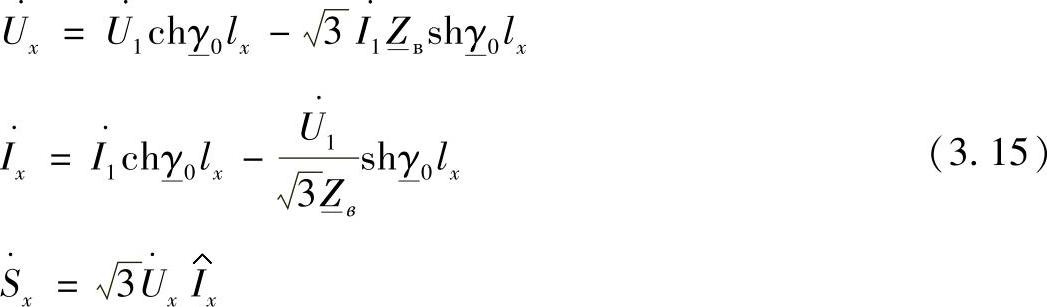
三相线路的末端

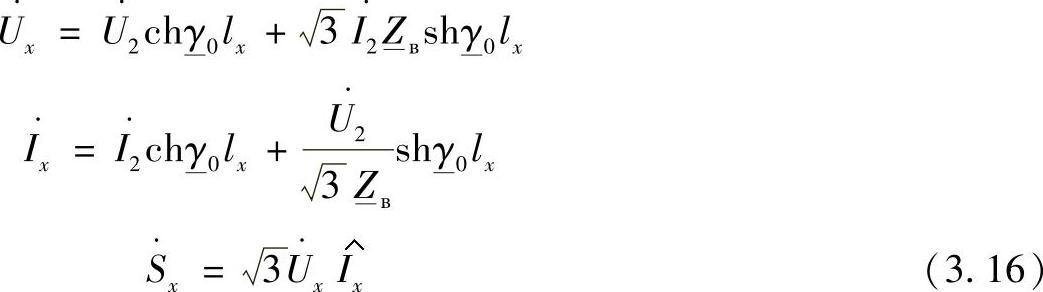
按照式（3.15）和式（3.16），令l_x=L，可以求出线路首、末端的相电流、相电压和功率。

上面得到的式（3.7）和式（3.8），是在将线路任一中间点电流和电压作为互为相反方向注入的两个波（入射和反射）的基础上推导而来的。这个方程右面部分的第一项是入射波，第二项是反射波。此理论可以用来对线路的不同状态进行分析，包括暂态。但是，当解决实际的工程问题时通常将电流和电压作为一个统一值，而没有将它们分成不同的分量。