相结构参数的优化选择方案

通常所使用的描述相结构的参数包括：导线数量及其间距。

首先，相结构参数的选择是按照设计电流确定单相导线的总截面积（设计电流是以线路运行5年的电流值为基础计算出来）；其次，在满足总截面积要求的情况下，确定几种标准型号的导线数量组合。例如，当总横截面积为2000mm左右时，可以有以下几种组合：4mm×500mm，5mm×400mm，7mm×300mm等等。对于已选择的导线，在假设的线路敷设区域环境温度下，按照一定顺序进行短路电流热稳定校验。

然后，每一个方案确定最优的分裂间距a，并计算最大的电场强度E_max。E_max要与电晕产生针对的初始电场强度和无线电干扰条件下的电场强度允许值相比较，如果已选择的方案满足上述条件，再确定导线的热损耗、挂冰及风载荷。

对所有方案进行类似的计算，在经济技术比较的基础上选取最优的方案。

以n个按照正多边形顶点分布导线（见图2.5）构成的相结构为例，其具有以下参数：

Rр为分裂半径，是正多边形外接圆的半径，正多边形的顶点对应导线的中心；

a为分裂间距，是每相相邻导线中心之间的距离；

rэ为等值导线的半径。

分裂半径和分裂间距之间的关系可以由图2.5得出

严格地说，在每相n根导线的情况下，还应该考虑线路其他相所有导线的影响，这样将使数学描述非常复杂。因此，以一个半径为rэ的等值导线来描述分裂相是更方便的，这样可以假设每相所有导线的电流相等。这个假设是有根据的，首先相间间距是每相导线之间距离的10倍，因此可以认为其他相电流在本相各个导线上所感应的电动势是相等的；其次，每相的各导线是按照正多边形的顶点均匀分布的，可以认为它们之间的相互影响也是相同的。

等值导线的半径可以认为是一根导线到其他所有导线之间距离的几何平均值，即

式中 Пd_1i——每相第一根导线到其他所有导线之间距离的乘积。

上述计算表达式还有如下的形式：

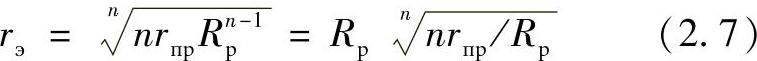
因为每相所有导线的工作电压、电流是相同的，每相的总电荷在所有导线中是均匀分布的，所以每根导线的电荷为

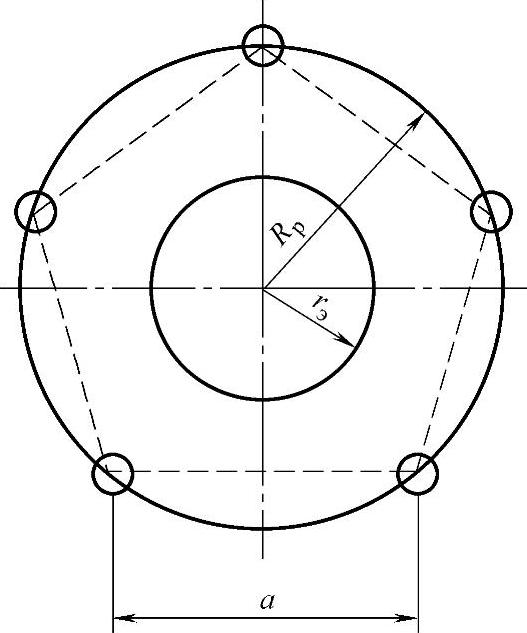
图2.5 常规的相结构

因为所有导线上的电荷符号相同，由于这些电荷的相互作用，每根导线所产生的电场将是不均匀的。每根导线最大电场强度是在多边形外部方向的表面上，最小电场强度位于导线内部方向的表面上。不同导线数量的分裂相电场分布如图2.6所示。在图2.6所列出的各种情况下，每根导线的电场都是非常不均匀的，但是随着导线数量的增加，每相的总电场是越来越均匀的。

图2.6 分裂导线电场结构示意图

导线表面（见图2.7）的电场强度可以描述为3个分量：最大电场强度E_max、最小电场强度E_min和平均电场强度Eср，平均电场强度是按照式（2.1）确定的对应单芯导线的电场强度。

如果计及真空和空气的介电常数，导线的电容以单位_μF/km表示，电压为经常使用的线电压值，每相导线平均电场强度的幅值可以按照式（2.9）计算

式中 С_р^ср——中间相电容（μF/km）；

U——经常使用的线电压值（kV）；

n——每相导线数；

r_пр——导线半径（cm）。

当导线水平排列时，应该考虑中间相与两个边相之间的电容比边相之间的电容大，中间相的工作电容比边相的电容大5%～7%。由此，中间相的电场强度越大，导线的电晕电能损耗和无线电干扰的程度越大。因此，所有计算都是以中间相为基础的。

中间相的工作电容，μF/km，可以表示为

式中 Dсг——输电线路相间的几何距离，Dсг=

当输电线路水平排列时D_сг=1.26d₁₂。

导线外部表面的最大电场强度为

式中 k_н——电场的不均匀系数，对于在此被研究的分裂导线相结构按照如下表达式确定

图2.7 分裂导线电场强度的构成

对于常规相结构，电场的不均匀系数总是大于1的，实际当中取为k_н≈1.1～1.15。因为每相导线之间的相互影响取决于其间距，那么导线表面的电场强度同样是此距离（分裂间距）的函数。

分裂间距的变化导致每相导线相互作用程度的变化，最终使得每根导线表面最大电场强度发生变化，但此过程也存在两个因素之间的反作用。分裂间距的增加增大了等值导线的半径，因此相电容也增大了，E_ср值也增大了。从另一个角度来说，此时电场的不均匀系数降低了（k_н→1）。

图2.8 750kV线路不同导线数量时最大 电场强度与分裂间距的关系

当一相的导线数量增加时（保持总截面积不变），因为相电荷分布在了更大的表面积上，最大的电场强度降低了，不同导线数量时最大电场强度与分裂间距的关系E_max=f（a）如图2.8所示。此导线之间间距的最小值、也是最优值a_опт的表示并不清晰。

为了消除总电晕，必须在a=a_опт时满足式（2.4）。对于每相三根导线的500kV线路，通常a_опт=22～25cm。因为在a_опт上最小电场强度表示得不清晰，很难精确地确定其具体数值，因而允许a_опт存在一些偏差。

在选择分裂导线结构时还必须考虑其气体动力学特性。在水平阵风时，在线路附近的垂直方向上附近，每根导线后面都产生一个空气涡流区域，如果相邻的导线落到这个区域，就会产生不利的振动，导致其部分金属丝的断裂。因此，要求导线间距不小于（10～12）d_пр，d_пр为导线直径。

对于分裂导线来说，术语“总电晕”的产生是有条件的，因为电晕只是出现在每根导线的外部表面，而不是占据导线的全部表面。(www.xing528.com)

按照上面的表达式可以得到电晕产生时的允许电压Uдоп кор，并可以将之与电场强度计算点的线路工作电压相比较。

当电晕刚好发生时，将式（2.5）、式（2.10）、式（2.12）代入到式（2.9）中，U_{доп кор}=0.9U_кор，其中U_кор为总电晕产生时的电压，有

工作状态下的最大的电场强度被确定为

式中 U_раб——工作状态下的电压。

综合这两个表达式，得到

或者

按照上述表达式可以确定计算点在线路不发生电晕情况下的电压裕度。当最大负荷状态下的变电站母线电压等于最大工作电压时，线路的起点和终点可以被作为计算点；当最小负荷状态下线路中间点的电压可能超过其端点电压时，则选取线路中间点作为计算点。

在上面已经阐述过了，超高压输电线路的电晕放电往往伴随着不间断的脉冲电流，导致高频电磁辐射的产生，电磁辐射的强度与电场强度直接相关，此电磁辐射在很宽广的频带内也是无线电干扰源。

输电线路上的电晕干扰可以分为如下两种类型：

1）由输电线路辐射产生的无线电干扰，并作用于输电线路附近的收音机、电视机和无线电台的天线；

2）沿输电线路传播的干扰，将破坏通信、遥测和继电保护高频通道的正常工作。

对于330～500kV和750kV架空线路，根据允许的无线电干扰水平，可以按照下列公式确定电场强度：

E_доп=31.1-17.4lgr_пр

E_доп=32.2-17.4lgr_пр （2.16）

在上述电场强度下，波段为0.15～30MHz、在距离最边缘的超高压输电线路导线投影100m范围内、一年中不少于80%时间内的无线电干扰水平不应该超过允许值。

在相关设备的设计和制造过程中，包括在恶劣气候条件下通过使允许的信号干扰超过一定的量（包括恶劣天气情况），来保护输电线路高频通道免受干扰。

在大学的教学实践过程中，存在如何按照电晕和无线电干扰校验输电线路相结构的问题，此时需要提供所有的原始数据，包括导线数量、分裂导线的半径、分裂间距、相间间距、导线的光滑系数（在相应的天气条件下）和相对空气密度。在计算中所使用的状态量——电压值，是按照所要解决问题的要求而设置的（计算点、计算所要求的运行方式），也可以是额定电压、最大的计算电压或者最大的工作电压，以及最小负荷下线路中间点的电压。最后，分别按照电晕产生时的条件（2.2）～（2.4），以及无线电干扰条件（2.16）确定允许的电场强度。

最大电场强度Е_max（需提供的数据：导线数量n、分裂间距a、导线半径rпр、相间几何间距Dсг）的计算算法如图2.9所示。

图2.9 最大电场强度计算和按照电晕及无线电干扰校验相结构的算法

下面阐述分裂导线最佳导线数量的确定方法。如上所述，对于通常的相结构来说，电荷的分布是不均匀的。随着导线数量的增加，不均匀的程度也增加，电荷被排除到导线的外部表面，导线的利用率降低，最终使得线路的自然功率增量降低。线路的自然功率是度量其输电能力的量，当导线数量从4根增加到5根时，自然功率增量是5%左右；进一步增加导线数量——从5根增加到6根，自然功率增量也仅仅为2.5%。（见表2.1）。因此，在达到一定的限值之后，进一步增加导线的数量是低效率的。

表2.1 750kV分裂导线数量对其参数的影响

（续）

当导线数量确定后，还需要考虑导线重量、挂冰载荷和风载荷的增加，以及与此相关的塔架和基础要求，这些都需要增加线路的投资。除此之外，输电线路电气参数的改变会导致补偿设备功率的变化，这同样被反映在输电线路的经济性指标中。

分裂导线的使用：一方面降低了电晕损耗；另一方面增加了线路的投资，同时增加了补偿设备的成本。因此，只考虑上述两方面中的一个是不对的。采用对一系列相结构进行经济技术比较的方法以及根据在实验场地的试验和实际敷设的经验来解决这个问题。最佳相结构的确定常常是针对重新确定电压等级或者是与传统相结构有偏差的线路进行的。

对于在俄罗斯已经使用的330～750kV电压等级超高压输电线路，每相的导线数量为

注：对于1150kV输电线路相结构没有被最终确定，因为其建造和运行的经验不足。

只有在特殊的情况下才会减少每相导线的数量：330kV线路每相减少一根导线，500kV线路每相减少2根导线。例如在挂冰载荷和风载荷很大时，在山区还要考虑设备运输和安装困难等因素。

如果相间距离增加到1m左右，可以忽略分裂相各导线电磁场之间的相互影响，认为电荷在导线表面的分布是均匀的。此时输电能力与每相导线的数量成正比，可以以下面的示例来解释。

对应自然功率下的相电流可以表示为

I_ф=qv

式中 v——电磁波在线路中的传播速度；

q——电荷。

q=Е_доп2pε₀εr_прпk_исд

式中 k_нсл——每根导线表面电荷分布的导线利用率， （2.17）

由此，线路的自然功率可以由下式确定：

P_нат=3U_cpI_Ф=3U_Ф2πE_лои ε₀ εr_пpnk_исп （2.18）

在此k_исп≈1，并且自然功率（输电能力）正比于导线数量。

图2.10表示了功率与每相导线数量的关系。从图2.10和式（2.18）可见，通过增加分裂导线的数量，使得采用非传统结构的导线线路输送能力提高了。但是，这些线路还有一系列结构上的缺点，目前处于研究阶段。

在超高压输电线路上，考虑到导线的机械强度及其工作的可靠性，不推荐使用。截面积在240mm²以下的线路。除此之外，不管是否为分裂导线，其截面积都需大于按照电晕产生条件所限制的最小导线截面积。