共轭凸轮打纬机构设计原则与步骤

共轭凸轮打纬机构的设计，包括根据打纬工艺的要求，确定筘座的动程βmax，在后死心处筘座的静止时间φt，设计从动件的运动规律，然后根据运动规律、空间条件、机构最大压力角αmax等要求设计凸轮机构，包括凸轮基圆半径、摆杆长度及主副摆杆之间的夹角、凸轮转动中心与摆杆摆动中心之间的距离等。当筘座运动规律设计好后，就要根据实际情况确定主、副摆杆的长度l1、l2及主、副摆杆之间的夹角γ，然后在保证最大压力角在许用范围之内的条件下确定凸轮转动中心至摆杆摆动中心之间的距离a，最后设计出凸轮轮廓曲线。

（一） 确定凸轮和摆杆的中心距a

如图10-20 所示，设O1为凸轮转动中心，O2为摆杆摆动中心，A 点为主从动杆转子中心。当凸轮绕O1点转动时，转子中心A 点受到凸轮的作用力F12，该力沿凸轮理论廓线的法线方向。A 点的速度v2则垂直于摆杆O2A。F12与v2之间所夹的锐角就是此时凸轮机构的压力角α。另外，根据三心定理，凸轮与摆杆的速度瞬心P12是凸轮理论轮廓线在A 点的法线与O1O2连线（或其延长线）的交点，分别如图10-20（a）和图10-20（b）所示。连接AP12，并过O1点作AP12的平行线，交于O2A（或其延长线）于B 点。则有以下关系存在：

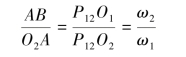
因此：

由机械原理知，当ω2、ω1转向相反时，瞬心P12在O1O2的连线上，B 点应在O1A 的延长线上[图10-20（a）]；而当ω2、ω1转向相同时，瞬心P12应在O1O2的延长线上，B 点应在O1A 的上[图10-20（b）]。因此，在式（10-52）中引入“-”号，表示AB 与O2A 的方向之间的关系，则（10-52）转化为：

图10-20　凸轮和从动件转向与瞬心位置的关系

由式（10-52）可知，AB 线段长度等于从动杆上滚子转动中心线速度vB与凸轮角速度ω1的比值。若给定凸轮机构的许用压力角为[α]，在机构运动的某一时刻，根据ω2、ω1的转向关系，自A 点在O2A 或O2A 的延长线上量取线段AB，使其大小等于上述瞬时速比，可得到B点。再自B 点作两直线，使其与O2A 分别成90°-[α]和90°+[α]（称为边界线），如图10-21 所示。如果凸轮转动中心就设在此两条直线上，则凸轮的压力角均等于[α]。而在此两直线所夹区域内，凸轮压力角将小于许用压力角[α]，此区域即为该时刻凸轮转动中心的理想设置区。将凸轮机构一个运动周期内各时刻所对应的两根边界线都绘出，这一系列边界线所包围的共有区域就是满足α＜[α]要求的凸轮转动中心理想设置区，叫作凸轮转动中心的可行域。且如图10-21 所示，若凸轮转动中心O1设在摆杆O2A 的下方，则边界线取下半部分（O1下所在区域），反之，若凸轮转动中心O1设在摆杆O2A 的上方，则边界线取上半部分（O1上所在区域）。

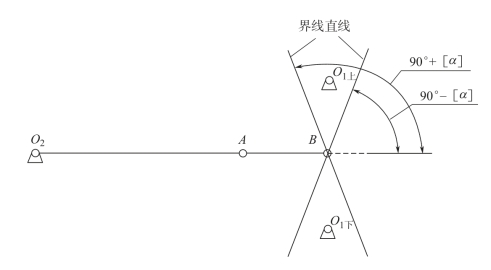
图10-21　凸轮转动中心可行域边界线

由于共轭凸轮机构的主从动杆与副从动杆固结在一起，它们的运动规律完全相同，因此，通过上述方法所求出的主、副凸轮转动中心可行域图形完全一致，如图10-21（a）中所示，左一区域与右一区域的线条族所围区域为主凸轮可行域；左二区域与右二区域的线条族所围区域为副凸轮可行域。图中右二与左二区域内线条族分别为左一与右一区域内线条族绕中心O2顺时针旋转γ 角所得。为清楚起见，只画出四个曲线族的包络线，如图10-21（b）所示，结合图（a）（b）可知，求解共轭凸轮转动中心可行域时，只需绘制主凸轮可行域边界直线族所围区域，即图10-21（b）中曲线1、4 和曲线2、3 所围区域，再将曲线2、3 绕O2点顺时针旋转γ 角（主、副从动杆夹角）得曲线2´和3´，2´、3´两曲线所围区域即为副凸轮转动中心的可行域。两边界直线族所围共有区域[图10-21（c）中阴影区域]即为满足许用压力角要求的共轭凸轮转动中心可行域。

图10-22（c）中四条曲线的求解方法如下。

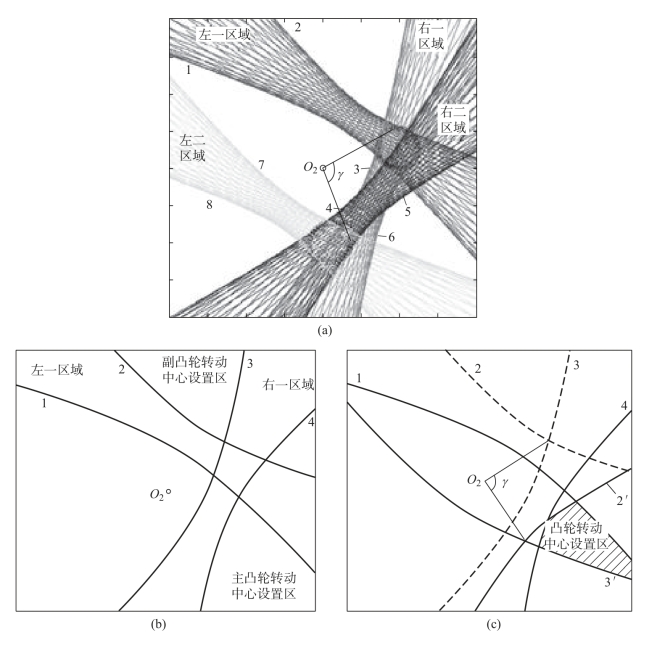
图10-22　凸轮转动中心可行域求解

如图10-23 所示，将从动件转动中心O2设为极点，从动杆起始位置O2A0为极轴。设从动杆任意位置O2A 摆角为φ，此时对应的边界线为UU´，Q 为此直线上任意一点，该点的向径为ρ，极角为λ。取O2A＝1，由式（10-53）得，。作O2D⊥UU´，则：

图10-23　凸轮转动中心的可行域

在ΔO2QD 中，

无限接近直线方程为

其中，φ´＝φ+dφ，e´＝e+de。

将式（10-54）与式（10-55）相减，得：(www.xing528.com)

将式（10-54）和式（10-56）两边平方后相加得：

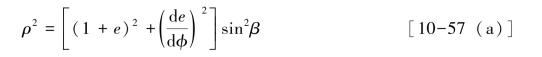
将式（10-54）和式（10-56）相除得：

而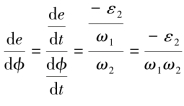，代入式（10-57），可求得凸轮转动中心可行域边界包络线方程式为：

在上式中，ε2为从动件角加速度，β 取90°-[α]或90°+[α]（选取规则在后文讨论）。

分别将推程和回程从动件运动参数（角位移φ、角速度ω2和角加速度ε2）代入式[10-58（a）]和式[10-58（b）]，即可求得极坐标下凸轮转动中心设置区。

在利用计算机求解式[10-58（a）]和式[10-58（b）]及绘图求解转动中心可行域时，应注意以下几个问题。

（1）在推程或回程起始和终止时刻摆杆角速度ω2为零，但sinβ 不为零，因此由式[10-58（a）]得ρ 为无穷大。为了提高计算机绘图的效率，可将起始时刻摆杆摆角设为φb+ξ，终止时为φe-ξ（其中ξ 为大于0 的一个很小的数据），从而避免因ω2为零而引起ρ 无穷大现象。

（2）因ω1恒定，β 不变，由式[10-57（a）]可得ρ 为常量，所以此时4 条包络线为4段以O2为圆心的圆弧，无法求出凸轮转动中心的设置区。解决办法是，先通过式[10-58（b）]求得λ，再代入式（10-53）求得ρ，问题得到解决。

（3）通过式[10-58（a）]和式[10-58（b）]或式（10-54）和式[10-58（b）]计算图10-22（c）中4 条包络线时，β 的取值见表1。

表10-2　β 取值表

注 当凸轮转向与从动件推程运动方向相同时η＝1，反之η＝-1。

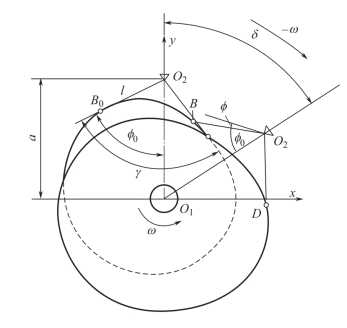
图10-24　共轭凸轮廓线求解示

（4）因图10-22（c）中曲线2、3 由图10-22（b）中曲线2、3 顺时针旋转γ 角获得，实际计算机计算时ε 值应取ε-γ。

（二） 共轭凸轮廓线方程

下面采用反转法推导凸轮廓线方程。如图10-24 所示，取凸轮转动中心O1为原点建立直角坐标系，y 轴经过凸轮转动中心O1和从动件转动中心O2。O1到O2的距离为a，从动件杆长为l，主、副从动杆夹角为γ，凸轮以ω 逆时针旋转，从动杆O2B 起始角为φ0。在反转运动过程中，当从动件相对凸轮转过δ 角时，从动件处于BO2D 位置，此时其角位移为φ（规定构件逆时针转为正，顺时针为负），则B、D 点坐标分别为：

式（10-59）、式（10-60）即为共轭凸轮理论廓线方程。设滚子半径为R，则共轭凸轮工作廓线方程为：

式中，

计算主、副凸轮工作廓线时，求得凸轮理论廓线坐标x、y 及对应dx/dδ、dy/dδ，联立式（10-61）和式（10-62），即可求得共轭凸轮工作廓线方程x´、y´。