凸轮机构从动件运动规律解析

凸轮机构中组合式运动规律是由基本形式运动规律（三角函数运动规律、多项式运动规律）根据边界条件组合设计而成的，在《机械原理》《机构学》的书籍中都有论述，这里不再详细介绍，只是给出各种运动的表达式和特点。本节主要介绍组合式运动规律的设计过程。

（一） 三角函数运动规律

1.简谐运动规律（余弦加速度运动规律）

当一点沿圆周做等速运动时，该点在圆周直径上的投影运动称为简谐运动。若从动件运动规律为间歇运动，则其位移、速度和加速度与凸轮转角的关系表达式为：

式中：h 为直动从动件的动程；φ0为与h 相应的凸轮转角；φ 为某一时刻凸轮的转角；ω 为凸轮的角速度（常数）；s 为从动件的线性位移；v 为从动件的速度；a 为从动件的加速度。

以下关于凸轮从动件的运动规律方程中，如没有特别说明，各个符号的含义同上。

从式（10-38）可以看出，从动件做简谐运动时，其加速度按余弦规律变化，所以简谐运动又称为余弦加速度运动。

图10-13 为余弦加速度运动规律的位移、速度和加速度曲线。当凸轮角转过φ0角度，从动件从起始位置上升一个动程h，其加速度曲线相当于余弦曲线的半个周期。若将此运动规律用于“停—升—停”型运动，则从动件的加速度在起始和终止时刻不连续，机构将产生柔性冲击，故该运动规律仅适用于中低速。若将该运动规律用于“升—降—升”型运动，即两个运动周期之间从动件没有停歇过程，则加速度曲线成为连续曲线，如图10-14 所示，不存在柔性冲击，可用于高速。

2.正弦加速度运动规律

这种运动规律的加速度方程式为整个周期的正弦曲线，其位移、速度和加速度的表达为：

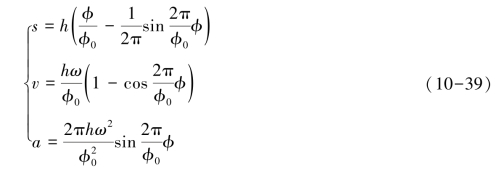
图10-15 为正弦加速度运动规律的位移、速度和加速度曲线。将其用于“停—升—停”型运动，从动件在起始和终止位置的加速度无突变，即无柔性冲击，运动平稳。

图10-13　简谐运动曲线

图10-14　简谐运动用于“升—降—升”型运动

（二） 多项式运动规律

多项式运动规律的位移方程式一般表达为：

图10-15　正弦加速度运动曲线

式中，C0、C1、C2、…Cn均为系数。常用的多项式运动规律有等速运动、等加速运动、等减速运动和五次多项式运动。

1.一次多项式运动（等速运动） 规律

一次多项式运动规律的速度曲线是一条水平直线，故又称为等速运动规律，曲线如图10-16 所示。这种运动规律用于“停—升—停”型运动，从动件在始、末位置分别有正、负无穷大的加速度，产生理论上无穷大的惯性力，出现所谓刚性冲击。所以单纯采用等速运动规律以实现“停—升—停”型运动是不合适的，需要在此基础上进行改进。

2.二次多项式运动（等加速、等减速运动） 规律

二次多项式运动规律由两段组成，即等加速段和等减速段，其中，等加速段的位移、速度和加速度表达式为：

图10-16　等速运动规律曲线

等减速段的位移、速度和加速度方程式为：

二次多项式运动规律曲线如图10-17 所示。等加速等减速运动规律。

在起始点和终止点虽然没有速度突变，但在这两点及中点仍有加速度突变，即存在柔性冲击。在高速条件下，振动、冲击仍较剧烈，因而在一定程度上限制了这种运动规律的应用。

3.五次多项式运动（等速运动） 规律(www.xing528.com)

五次多项式运动规律的表达式为：

图10-18 所示为五次多项式运动规律的运动曲线，由图可见，其加速度变化比较缓和，因而常在较高速度的凸轮机构中应用。

图10-17　等加速等减速运动规律曲线

图10-18　五次多项式运动规律曲线

用同样的方法，可以得到从动件回程时的运动方程为：

对于更高次方的运动规律，如七次多项式运动规律，再添两个系数，可相应增加两个边界条件，以控制从动件在始、末位置的跃度（加速度的导数）。推导方法与上述相同。

（三） 组合式运动规律

为了消除上述单一运动规律中存在的刚性冲击或柔性冲击，将两种或两种以上的单一运动规律按照一定的原则进行组合，可得到组合运动规律。为了消除冲击，在两种运动规律的连接点处，要保证它们的位移、速度和加速度分别相等，这就是两种运动规律进行组合时应满足的边界条件。

下面以正弦加速度与等速运动规律的组合为例进行分析。

等速运动规律的从动件在运行的过程中速度平稳，加速度为0，故对机构的运行有利，但其在运动的始、末存在刚性冲击。如果单一采用该运动规律，将会在运动的起始和终止时产生巨大的惯性冲击，对机器极其不利，所以须进行改进。改进的方法是，在运动的始、末两端用正弦加速度曲线、余弦加速度曲线或其他曲线进行光滑连接。

下面介绍用正弦加速度运动规律对其进行修正的方法，其他的组合方式可参考此方法进行。

正弦加速度与等速运动规律组合的位移、速度和加速度曲线如图10-19 所示，φ1、φ3为正弦加速度对应的凸轮转角，φ2为等速运动规律对应的凸轮转角。通常，取φ1＝φ3＝φ0/4，即升程运动的一半时间为正弦加速度运动，且分布在前四分之一和后四分之一段。因为这种组合运动规律在始、末两点处的加速度均为零，可用于工作行程需等速的“停—升—停”运动。

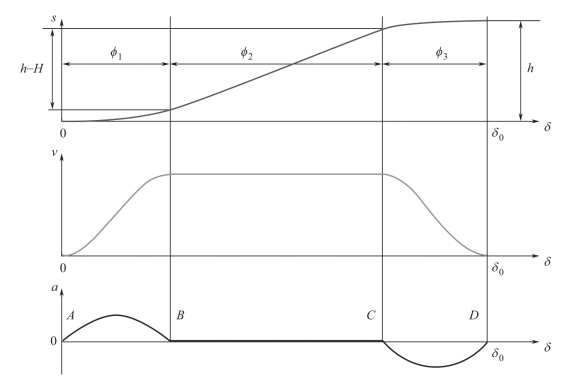
图10-19　正弦加速度与等速运动规律组合

设正弦加速度运动所对应的从动件位移（AB 段和CD 段位移之和）为H，则以φ0／2 和H分别替换式（10-39）中的φ0和h，有：

在B 点处，φ＝φ0／4，带入式（10-46），可求得B 点处从动件的位移、速度和加速度：

对于BC 段，可直接应用式（10-40），并用上述相同的方法确定：C0＝H／2，C1＝4H／ φ0。这样，等速运动的规律可写为：

当凸轮转过整个升程运动角的一半，即φ＝φ0／2 时，从动件也运动到升程的一半，即s＝h／2，把这个对应关系带入代入式（10-46）得H＝h／3。依次代入式（1-46）和式（10-48），就可以得AB 段和BC 段的运动方程式。

AB 段：0≤φ ≤φ0／4

BC 段：φ0／4≤φ ≤3φ0／4

根据对称关系进一步导出与AB 段对称的CD 段的运动方程式。

CD 段：3φ0／4≤φ ≤φ0

各种单一运动规律及组合型运动规律的最大速度vmax和最大加速度amax如表10-1 所示，表中还列出了各种运动规律的荐用范围，供选择从动件运动规律时参考。

应注意的是，上述各种运动规律方程式都是以直动从动件为对象来推导的，如为摆动从动件，则应将式中的h、s、v 和a 分别更换为动程角βm、角位移β、角速度ω 和角加速度ε 。

表10-1　各种运动规律特性比较