针织机的三角实际上就是一个个凸轮,而织针是做直线往复运动的从动件,因此,三角的设计也就像设计凸轮廓线一样,在满足工艺要求的基础上,织针的速度变化率(加速度)尽可能小,从而使织针运行平稳,避免惯性力引起的冲击,使机器运行平稳并延长织针的寿命。常用的三角廓线为曲线,可以是单一的多项式曲线,也可以是组合式曲线。
图8-17 为一组三角的位移曲线,与图8-14 相同,AB 段为挺针三角,高度为HB,宽度为dB;BC 段为压针三角,高度为HK,宽度为dK;CD 段是起针三角,高度为HP,宽度为dP。其中:
![]()
采用多项式运动规律时,必须分别设计AB、BC、CD 段,且B、C 和D 三个衔接点处,要保证织针的位移、速度和加速度曲线都光滑连接。
(一) AB 段(挺针三角) 的运动规律
建立如图8-17 所示的坐标原点在O 点的左手直角坐标系XOY,A 点是运动的起始点,织针从静止开始运动,即:
![]()
B 点是织针运动的最高点,速度和跃度(加速度的导数)也应该为0,即:
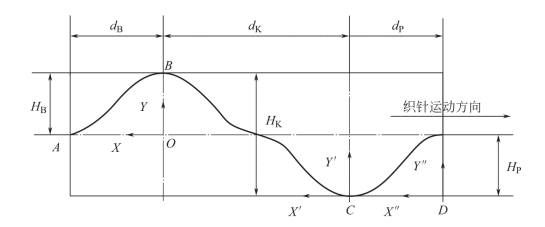
图8-17 三角位移曲线
![]()
从上面可以看出,在AB 段的边界条件有六个,因此可以采用五次多项式运动规律,其一般表达式是:
![]()
对式(8-21)分别求一阶导数、二阶导数和三阶导数,得:
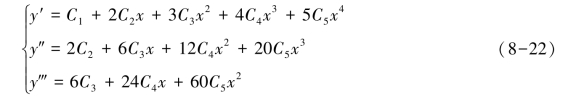
将B 点的边界条件(即x=0,y=HB,y´=0,y‴=0)带入方程(8-21)和方程组(8-22),可得:
![]()
将这三个系数的值及A 点的边界条件带入方程(8-21)和方程组(8-22),可得方程组:
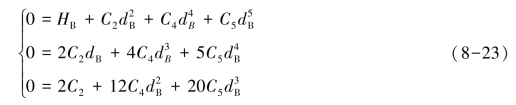
将方程组(8-23)写成矩阵形式:
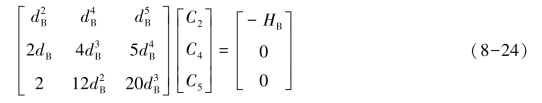
解上述方程组,得:

因此,由式(8-21)得AB 段(挺针三角)的位移曲线方程为:

在B 点,挺针结束,此时,织针的加速度为:

(二) BC 段(压针三角) 的运动规律
在图8-17 中,建立直角坐标系X´CY´,其坐标原点在C 点,B 点是压针运动的起始点,同时也是挺针运动的最高点,故有:
![]()
C 点是压针运动的终止点,应满足:
![]()
从上面可以看出,在BC 段,边界条件有七个,因此可以采用六次多项式运动规律:
![]()
该方程的一阶、二阶、三阶导数为:

将C 点的边界条件带入式(8-26)、方程组(8-27),可得:
![]() (https://www.xing528.com)
(https://www.xing528.com)
则式(8-26)和方程组(8-27)变为:
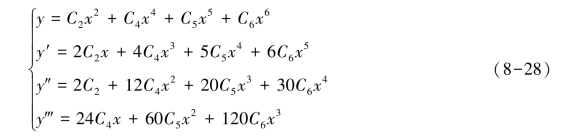
将B 点的已知条件(x=dK,y=HK,y´=0,y″=Q,y‴=0)带入方程组(8-28),得方程组:
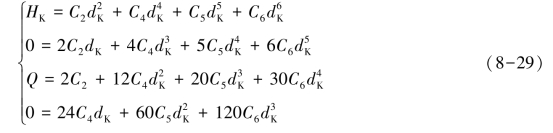
将方程组(8-29)写成矩阵形式:

解该方程组,得:

因此BC 段曲线的方程为:
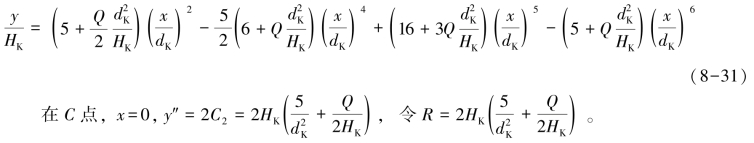
(三) CD 曲线(起针三角) 的运动规律
如图8-17 所示,建立坐标原点在D 点的左手直角坐标系X″DY″,C 点是起针运动的起始点,也是压针运动的终止点,故有:
![]()
D 点是起针运动的终止点,应满足:
![]()
从以上分析可以看出,在CD 段的边界条件有七个,同样可以采用六次多项式运动规律:
![]()
该方程的一阶、二阶、三阶导数为:

将D 点的边界条件带入式(8-32)、方程组(8-33),可得:
![]()
式(8-32)和方程组(8-33)可变为:

将C 点的已知条件(x=dP,y=0,y´=0,y″=R,y‴=0)带入方程组(8-34),得方程组:
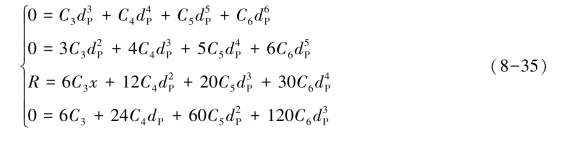
将上述方程组(8-35)写成矩阵形式:
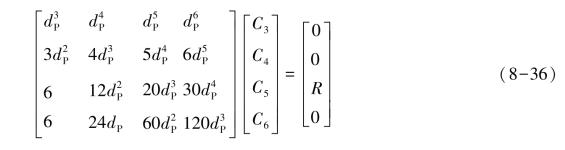
解该方程组,得:

其中,因此CD 段曲线的方程为:
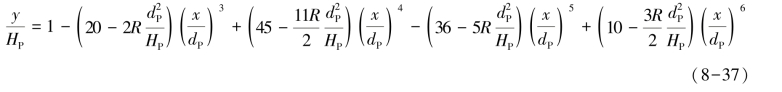
在已知HB,HP,HK和dB,dK,dP之后,就可以分别利用式(8-25)、式(8-31)、式(8-37)求得三角各段的位移曲线。
采用多项式运动规律的曲线三角,其位移、速度和加速度的变化是连续的,因此没有刚性冲击和柔性冲击,可以避免织针与三角之间的冲击,有利于提高机器速度。
但对于凸轮机构来说,衡量其传力性能好坏的一项重要指标是压力角。在织针的动程H*和织针三角横向宽度d*相同的情况下,曲线三角的最大压力角大于直线三角的压力角。同样,在最大压力角相同的情况下,若要实现织针动程相同,曲线三角的横向宽度要大于直线三角的宽度,这样,纱线在弯纱过程中被织针和沉降片弯折的次数就增多,会增加纱线上的张力。


图8-18 不同三角曲线的织针运动比较
图8-18(a)表示纱线的成圈过程,S 为沉降片,N 为针头。图8-18(b)表示不同最大压力角下直线三角和曲线三角控制的织针成圈过程,从图中可以看出,直线三角由于所占横向距离小,纱线在沉降片和针头之间弯曲的次数也少。图8-18(c)表示直线三角的纱线张力比曲线三角小。三角倾角(压力角)愈大,则纱的张力愈小。曲线三角所占的距离大,在弯纱过程中纱线弯折的次数多,因此张力较大。同样,最大压力角愈小张力就愈大。为了减小弯纱是纱线的最大张力,在采用曲线三角时,必须适当地减小纱线的初始张力。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




