管道内气流能量损失优化方法

空气在管道内流动时会遇到阻力，每输送单位体积气体的能量损失称管道阻力损失，用ΔPs表示，单位为Pa。它分为沿程阻力损失ΔPy和局部阻力损失ΔPj。

（一） 沿程阻力损失

空气在管道内流动时，由于黏性等原因而产生的摩擦阻力将阻碍其运动，因这种阻力存在于全流程，故将克服这种阻力造成的损失称为沿程阻力损失ΔPy。

式中：λ 为沿程阻力系数（由实验确定）；l 为风管长度（m）；v 为空气流速（m／s）；g 为重力加速度（9.81m／s2）；ρ 为空气密度（kg／m3）；ds为水力直径（m），即过流断面积（A）的4 倍与湿周x 之比，又称当量直径。对于圆形截面管道，ds＝d（过流圆截面直径）；对于矩形截面管道，ds＝2bh/（b+h），b 和h 分别是矩形的宽和高；对于正方形截面管道，ds＝h＝b。

沿程阻力系数λ 并不是常数，它与雷诺数Re、管壁相对粗糙度Δ/ds及过流断面形状有关。雷诺数Re＝ds/ν，ν 为空气运动黏度，它与温度、压力均有关。表7-2 表示空气在98.1kPa（1 工程大气压）下的运动黏度ν。

表7-2　空气运动黏度ν

图7-5 表示λ—Re 关系曲线，由实验测得。当空气作层流流动时（Re＜2300），在对数坐标下，λ 与Re 呈线性关系，且与管壁的粗糙状态无关。当空气作湍流流动时（Re＞2300），则λ 与管壁状态有关。曲线A 表示光滑管（包括铜管、铝管、玻璃管等）的λ—Re 曲线，曲线B 表示粗糙管（包括铸铁管、钢管等）的λ—Re 曲线。

图7-5　λ—Re 曲线

（二） 局部阻力损失

管道内气流急剧地改变流动状态，例如流经弯头、收缩管、扩放管、三通管、阀门等处，因发生涡流和脱流等现象而损失的流动能量，称为局部阻力损失，在数值上比沿程阻力损失大得多。局部阻力损失为：

式中：ξ 为局部阻力系数；ρ 为空气密度（kg／m3）；v 为空气流速（m／s）。

表7-3 示几种常见管件的局部阻力系数值。

表7-3　局部阻力系数表举例（计算公式中的v 应以图上所示的方向为依据）表7-3（1） 四节组成的90°弯管

表7-3　（2） 矩形90°弯头（不等截面） ——R/b=1， h/b=2.4

表7-3　（3） 矩形90°弯头（等截面）

表7-3　（4） 骤缩管与骤扩管（任意截面）

表7-3　（5） 锥形扩散管(www.xing528.com)

表7-3　（6） 锥形渐缩管

表7-3　（7） 调节闸门

表7-3　（8） 调节阀门

表7-3　（9） 正方形截面90°弯管（有导风板）

表7-3　（10） 金属网过滤板

上述的沿程阻力损失和局部阻力损失都属于纯空气流动时的能量损失。在气力输送中，空气内都混合有物料，应视为气物混合流，其密度并不等于纯空气的密度，在计算Δp 时结果也不相同，应乘上修正系数φ。从实验可知，此种混合流在流动中的能量损失比纯空气时有所增加，而且与物气比μ 值大小有关。

式中：α 为实验系数，它与物料性状有关，对于原棉α 可取1.5 左右。例如，对于物气比μ＝0.25 的气棉混合流，φ＝1+1.5 × 0.25＝1.375，即混合流在流动时沿程阻力和局部阻力损失均较纯空气流增大37.5%。

（三） 管道系统的特性曲线

在一个气力输送系统中，各段管道尺寸可能不同，应分段计算。总的沿程阻力损失应是各组成段沿程阻力损失之和，以∑Δpy表示。由于各段速不同，故应以qV/A 表示v，则得：

同样，总的局部阻力损失也是各个局部阻力损失之和，以∑Δpj表示：

因此，该管道总的阻力损失ΔPs为：

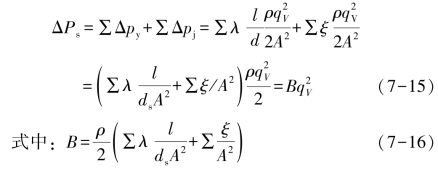
如果不考虑风量或风速对λ 和ξ 的影响，则对给定管道系统来说B 为常数，称为管道系统的阻力系数。式（7-15）表明，在确定的管道系统中，流动空气的阻力与其流量的平方成正比。根据这一关系绘出的曲线称为管道特性曲线，如图7-6 所示。图中两条曲线代表两种阻力特性不同的管道系统，曲线1 代表的系统的B 值小于曲线2 代表的系统。

图7-6　管道系统的特性曲线