粗纱卷装一般采用圆柱形平行卷绕,纱与纱之间相互紧挨着,故纱圈螺距就等于纱的直径或略大些(因粗纱受压而被压扁),这样可以获得密绕的卷装以提高卷装容量。其缺点是退绕时筒管必须回转(纱从横向抽出),会使纱产生意外牵伸,而且退绕速度较慢,所以不适用于细纱卷绕,因为不适应细纱高速退绕的要求,而且如果细纱采用圆柱形平行卷绕,各层纱容易嵌乱,不能分清层次,容易导致退绕困难。故细纱卷绕一般都采用圆锥形交叉卷绕,相邻两层纱圈螺旋线的交叉角虽不是很大,但纱圈螺距比细纱直径大得多。
无论是圆柱形平行卷绕,还是圆锥形交叉卷绕,为始终保证纱层厚度均匀,以维持应有的纱层曲面形状,按理想要求应把纱线绕成法向等螺距的螺旋线,即维持法向螺距hn为常值,以使纱在卷绕面上分布均匀。
在粗纱圆柱形卷绕时,如把纱的轴心线所在圆柱面展开为一平面,如图6-1 所示,则纱的轴心线在此展开面上将成为一倾斜直线AC,与周向展开线AB 之间夹角为α,则得:
![]()
式中:dk为卷绕直径;α 为螺旋线导角;hn为法向螺距。
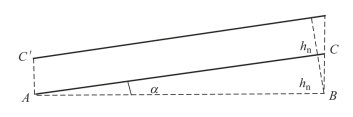
图6-1 圆柱面螺旋线展开图
另一方面,按几何关系应得:
![]()
式中:vh为导纱速度,即龙筋升降速度;V 为单位时间内的绕纱长度,即卷绕线速度或机器的单锭生产率。
当龙筋从B 点升到C 点时,纱就同时从A 点绕到C 点,上式表示在相同时间内两者的位移值应与各自的速度成正比,即BC/AC=vh/V。将上式代入式(6-1),得:

由式(6-2)可知,如要维持hn为常值,则vh与V 之间的比值必须与卷绕直径dk成反比。V 决定于前罗拉转速,vh由变速机构(常用铁炮变速)控制。因粗纱采用了圆柱形卷绕,在同一层中dk是不变的,故vh在同一层中也应不变,即导纱运动应作等速升降。在整个卷绕过程中,因dk逐层递增,故vh/V 应按式(6-2)的反比关系而逐层递减,故应该按这一规律进行变速机构的设计。
在环锭细纱机上进行圆锥形卷绕时,式(6-1)和式(6-2)同样也能适用,后面将证明。若把dk/hn作为横坐标,sinα 或vh/V 作为纵坐标,作出的图像是一条等腰双曲线,如图6-2 所示。这一规律可称为卷绕的双曲线规律,是粗纱和细纱卷绕往复导纱运动的共同规律。当然,除了这一共性外,它们之间也存在着一定的差别,主要有下面两点。
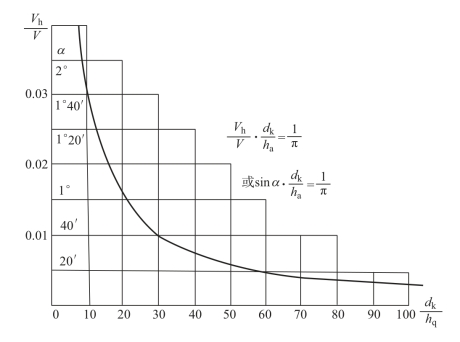
图6-2 双曲线规律
(1)在粗纱圆柱形卷绕时,hn约等于或略大于粗纱直径,而在细纱卷绕时,hn要等于细纱直径的好几倍。
(2)在粗纱圆柱形卷绕时,vh应随着dk的递增而逐层递减,但在每一层中的vh保持不变。而在细纱圆锥形卷绕时,则因每一层中的dk一直是在不断变化的,所以vh也应按式(6-2)所示关系在每一层中都要随dk的变化而不断变化。
细纱机采用恒速传动时,V 值不变,vh应与dk成反比关系而变化。但当细纱机采用整机变速传动时,V 本身也在变化,那么vh就不是简单地与dk成反比关系而变化了,而是速比vh/V 值或sinα 值要与dk成反比关系而变化,如图6-2 所示。按此规律进行卷绕,导纱运动就能获得圆锥面上的等距螺线,维持法向螺距hn值恒定不变,使纱在圆锥面上均匀分布。
根据以上分析可知,式(6-2)是粗纱或细纱两种加捻卷绕往复导纱运动的共同规律,故不论是粗纱变速铁炮或是细纱成形凸轮的设计,都是以此式为依据,以下两节将对此分别详细讨论。
下面研究各种类型加捻卷绕的回转运动,先研究它们的共同规律,然后再研究它们之间的差别或特殊规律。
设卷装转速(单位时间内的卷装转数)为nk,加捻转速(单位时间内所加的捻回数,即尚未绕到卷装上去的那段自由纱段的转速)为nt,则两者之差等于卷绕转速(单位时间内绕纱圈数)nh:
![]()
当卷装转速nk等于纱线转速(即加捻转速)nt,两者之间并无任何相对运动时,纱线不可能绕到卷装上去。只有在两者不相等(nk>nt或nt>nk)而有相对运动时,纱线才能卷绕上去,此时卷绕转速nh就应等于它们之间的相对转速(即差速)。
设卷绕线速度为V(即单位时间内卷绕长度或以长度表示的单锭生产速度),又设纱层卷绕直径为dk,则得卷绕转速为:
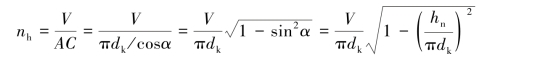
由于hn远远小于πdk,则:

因dk是变化的,故在V 不变时,nh应随dk成反比而变化,即在dk小时多绕几圈,dk大时少绕几圈。又因式[6-3(b)]与式(6-2)相似,也是双曲线规律,故有可能利用同一机构来同时完成vh和nh的变速要求。设前罗拉直径为dF,转速为nF,又如略去捻缩不计,则应得:
![]()
以上二式相除,得:
 (https://www.xing528.com)
(https://www.xing528.com)
再代入式(6-3),便得:

当nk>nt时左边取正号,nk<nt时则取负号。
式(6-4)左边dF是常值,但dk是变化的。故式(6-4)右边也必须相应变化,其变化情况可分为两类:①nt/nF不变,nk/nF随dk而变;②nk/nF不变,nt/nF随dk而变。
第一类即翼锭式加捻卷绕,加捻转速nt=锭速,这是因为锭翼固装在锭子上,纱则穿过锭翼臂绕到纱管卷装上去,故锭速即是纱线转速nt(=加捻转速),而纱线获得的捻度tw应等于:

itF表示锭速nt与前罗拉转速nF之间的传动比,是通过轮系传动来保证其恒定不变的。为适应对不同纱支有不同捻度tw的要求,在从前罗拉到锭子间的传动路线中设有变换齿轮,以变换itF的大小。当齿轮已换定后,那么在机器运转过程中itF是不变的,故tw也恒定不变,这就保证了产品捻度tw均匀的要求。
把式[6-5(b)]代入式(6-4),则得:
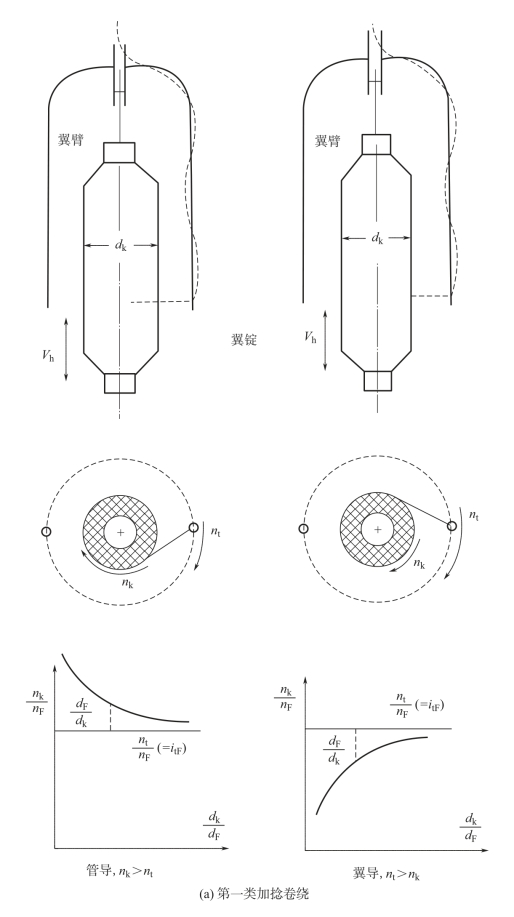
图6-3
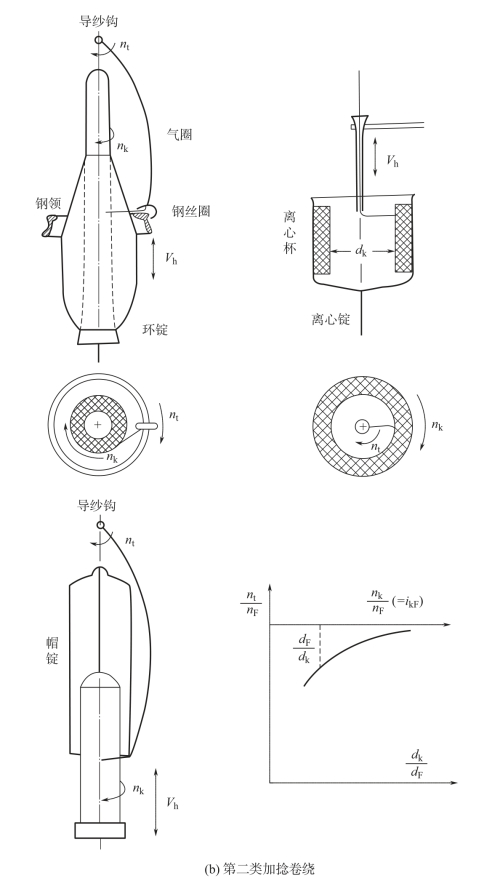
图6-3 加捻卷绕类型和转速规律
nk—卷装转速 nt—加捻转速 nF—罗拉转速 dF—罗拉直径

式中,右边的dk是变数,故nk/nF的速比就应按式(6-6)的关系随着dk的变化而变化。在翼锭式纺机上的筒管卷装是活套在锭子上的,其转速nk可以大于或小于锭速nt。前者称为管导(nk>nt),在式(6-6)中取正号;后者称为翼导(nt>nk),在式(6-6)中取负号。以上所述,示于图6-3(a)和图6-4(a)中。
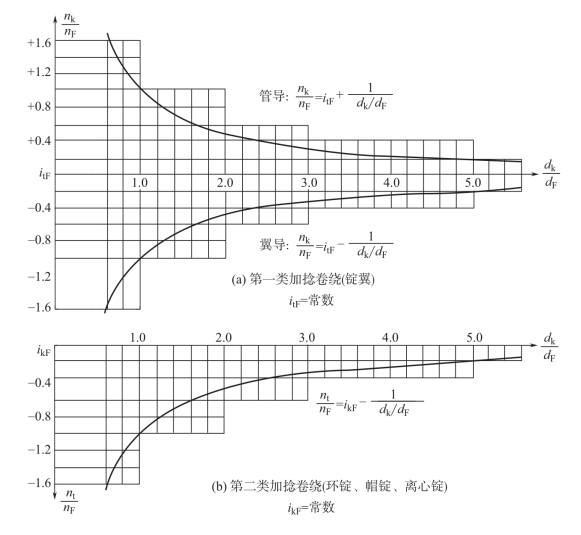
图6-4 加捻卷绕转速变化规律
nF—前罗拉转速 nk—卷装转速 nt—加抢转速 dF—前罗拉直径 dk—卷绕直径 ikF=nk/ nFitF=nt/nF
在管导时(nk>nt),筒管的变速必须采用积极传动,机构很复杂。在翼导时(nt>nk),则有可能利用纱线来拖动筒管,另在筒管底部施加一定的阻力以维持纱线张力,卷装转速nk就将随着dk的逐层递增而自动变化,不必采用积极传动,机构可大大简化,适用在毛纺、麻纺、绢纺机器上。但当纱线强度较弱,就不能用纱来拖动筒管回转。即使在翼导情况下,也必须通过变速机构来传动筒管。
第二类有环锭、离心锭、帽锭式加捻卷绕,其卷装转速nk就等于锭速,此时的卷装或锭子回转是通过恒速比来积极传动的,故卷装转速nk与前罗拉转速nF之间的速比应是恒值:
![]()
至于加捻转速nt,即纱线转速(指尚未绕到卷装上去的还在自由空间的那段纱线的转速),则并无任何机构积极传动,完全是靠卷装转速n 来消极拖动回转的,并由于摩擦阻力和空气阻力的作用,而始终落后于nk,即nk>nt,故在式(6-6)中应取正号,即相当于管导的情况。如把上式代入式(6-6),即得:

式中,右边dk是变化的,纱线转速nt则因受阻力控制而自动落后于nk,即按式(6-7)所示规律随dk的变化而变化,如图6-3(b)和图6-4(b)所示。因这一变化不必采用机构传动,与翼锭式积极传动的加捻卷绕相比,传动机构大大简化了。可是nt的变化却造成了纱线捻度也要跟着变化的问题,如把式(6-7)代入式[6-5(a)],可得:
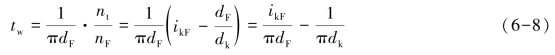
即捻度tw将随卷绕直径的变化而变化。设dk的最小值和最大值各为dmin和dmax,则得捻度差异为:
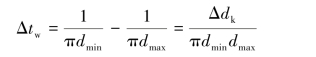
但差异率△tw/tw一般不大,影响很小。
在退绕时,纱线按轴向抽出,管纱不转,则每退一圈,将增加一个捻回,按单位长度计,将使捻度增加1/πdk,故得退绕后的捻度为:
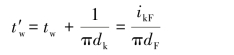
即捻度差异能在退绕后得到补偿。当然,为适应不同纱支,在卷装转速nk和前罗拉转速nF之间必须设有捻度变换齿轮,使ikF可以变换。但在运转过程中ikF是恒定不变的,故t´w也恒定不变。
在环锭和帽锭加捻时的纱线都形成气圈,气圏纱线的回转速度即是加捻转速nt。在离心锭加捻时并不形成气圈,但与气圏相类似,在导纱管出口到卷装的卷绕点之间有一自由纱段,此纱段的回转速度即是加捻转速nt。离心锭目前主要用在纺丝生产上。帽锭纺纱有一个缺点,就是在落纱时要先拔下锭帽,然后才能取出筒管,影响生产效率。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




