圈条容量计算及优化方法

当棉条以摆线形式存放在条筒中时，沿棉条筒直径方向棉层密度的分布很不均匀。图5-5 为条筒内棉层密度分布情况。气孔周围的圆环处（宽度为棉条直径）密度最高。棉条筒高度方向的空间利用，显然就取决于气孔周围这一最密圈内所能容纳的棉层数。在一定的卷装尺寸下，要提高卷装容量，就应尽量使各处棉层密度分布比较均匀。

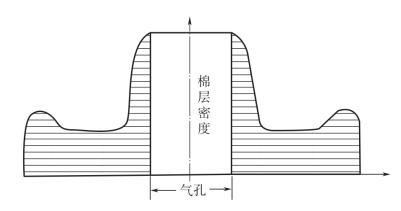
图5-5　条筒内棉层密度分布

棉条筒的理论容量为：

式中：G 为棉条筒所能容纳的棉条总重量；p 为单位长度的棉条重量；S0为棉条在条筒内的轨迹长度；H 为棉条筒高度+棉层允许突出条筒口的高度；t 为在气孔周围最密圈部分的单层棉条厚度；α 为棉条每绕一圈在气孔周围最密圈部分所对的圆心角。

将式（5-10）代入式（5-11），得：

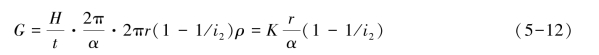
式中：K＝4π2ρH/t，对一定的卷装尺寸和棉条而言，K 为常数。

图5-6 中阴影部分为大圈条状态下每圈棉条与筒中最密圈的重叠部分，其所对的圆心角为α。因此，在厚度为t 的棉层中，最多可能容纳的棉条圈数为。

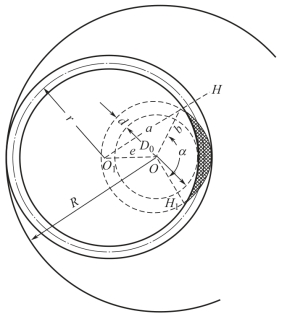
图5-6　卷装容量

R—棉条筒半径　D0—气孔直径　r—圈条轨迹半径（r＝R-e-r0）　e—圈条偏心距（e＝OO1）　d—棉条直径

现在求α。按照图5-6 中几何关系，可得：

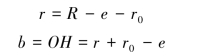(www.xing528.com)

将前式带入，得：

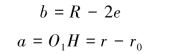
根据余弦定理，得：

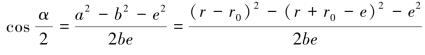
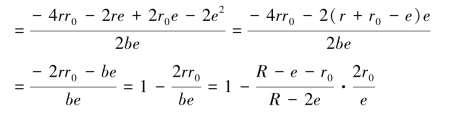
当e＝r0或带入上式，得：

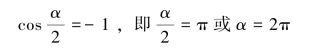
通过作图可知，当e＝r0时，圈条气孔为最大，仅仅靠筒壁部分有棉条，棉条的容量显然是最小的；当时，圈条的气孔已缩小为零，最密圈亦缩到最小，每增加一圈棉条，最密圈的厚度即增大一个t 值，棉条的容量亦受到限制。故如在上述两极限范围内，当e 取某一中间值时，就将使α 值为极小。

用微分方法对上列分式求导，并使其等于零，即：

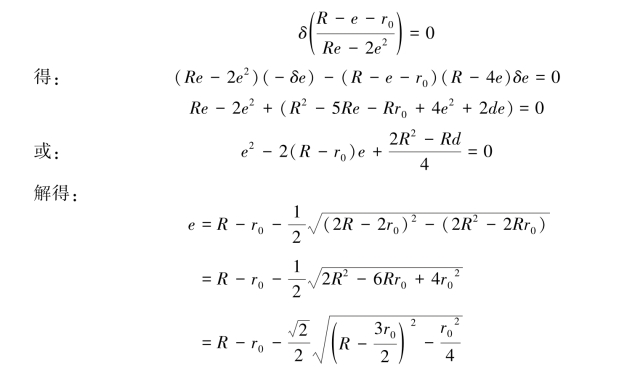
由于远远小于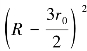，故近似可得：

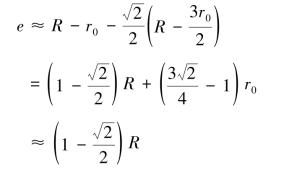
此时，α 值将是最小的。按式（5-12）可知，容量G 主要与r／ α 成正比，α 值最小当然对容量G 有利；但式中r＝R-e-r0，也与e 值有关，e 值越小，r 值越大。故实际上必须取e 值比上式之值更小些，才能获得G 的极大值。数学推算复杂，不易求得简单公式，但可用试凑法求解。

偏心值e 决定之后，可求得气孔大小为：